【概率论与数理统计】小结9-1 - 参数估计概述
注:在统计学的应用中,参数估计和假设检验是最重要的两个方面。参数估计是利用样本的信息,对总体的未知参数做估计。是典型的“以偏概全”。
0. 参数及参数的估计
参数是总体分布中的参数,反映的是总体某方面特征的量。例如:合格率,均值,方差,中位数等。参数估计问题是利用从总体抽样得到的信息来估计总体的某些参数或者参数的某些函数。
问题的一般提法
设有一个统计总体,总体的分布函数为$F(x, \theta)$,其中$\theta$为未知参数。现从该总体取样本$X_1, X_2, ..., X_n$,要依据样本对参数$\theta$作出估计,或估计$\theta$的某个已知函数$g(\theta)$。这类问题称为参数估计。
参数估计分类
- 点估计,其中点估计又可以分为矩估计和最大似然估计;
- 区间估计
例如,估计降雨量:预计今年的降雨量为550mm,这是点估计;预计今年的降雨量为500 - 600mm,这是区间估计。
1. 点估计的评价
由于存在不同的方法对总体中的未知参数进行估计,利用这些不同的方法得到的估计值也不同。因此就涉及到如何评价不同估计量的好坏的问题。
常用的评价准则有以下四条:
- 无偏性准则
- 有效性准则
- 均方误差准则
- 相合性准则
1.1 无偏性准则
无偏性是通过比较参数和参数估计量的期望来判断的。
定义:若参数$\theta$的估计值$\hat{ \theta } = \hat{ \theta} (X_1, X_2, ..., X_n)$,满足
$$E(\hat{ \theta }) = \theta, $$
则称$\hat{ \theta }$是$\theta$的一个无偏估计量。
若$E(\hat{ \theta }) \neq \theta$,那么$|E(\hat{ \theta }) - \theta|$称为估计量$\hat{ \theta }$的偏差,若$\displaystyle \lim_{ n \to \infty } E(\hat{ \theta }) = \theta$,则称$\hat{ \theta }$是$\theta$的渐进无偏估计量。
无偏性的统计意义:
无偏性的统计意义是指在大量重复试验下,由$\hat{ \theta }(X_1, X_2, ..., X_n)$给出的估计的平均值恰好是$\theta$,从而无偏性保证了$\hat{ \theta }$没有系统误差。
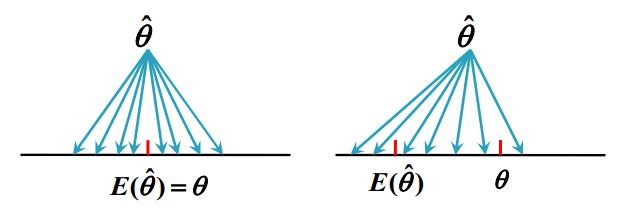
图1,无偏性
例如,工厂长期为商家提供某种商品,假设生产过程相对稳定,产品合格率为$\theta$,虽然一批货的合格率可能会高于0,,或低于0,但无偏性能够保证在较长一段时间内合格率趋近于$\theta$,所以双方互不吃亏。但作为顾客购买商品,只有两种可能,即买到的是合格产品或不合格产品,此时无偏性没有意义。
1.2 有效性
如果两种方法得到的结果都是无偏估计,那么这两种方法怎么区分好坏呢?这时候就可以用到有效性了。有效性是根据方差来判断估计值的好坏,方差较小的无偏估计量是一种更有效的估计量。

图2,有效性
1.3 均方误差
在实际应用中,均方误差准则比无偏性准则更重要!
定义:设$X_1, X_2, ..., X_n$是从带参数$\theta$的总体中抽出的样本,要估计$\theta$. 若采用$\hat{\theta}$作为参数$\theta$的点估计,则其误差为$\hat{\theta} - \theta$. 这个误差随样本$X_1, X_2, ..., X_n$的具体取值而定,也是随机的,因而其本身无法取为优良性指标. 我们取它的平方以消除符号,然后取均值,可得估计量$\hat{\theta}$的均方误差(误差平方的平均),
$$E[(\hat{\theta} - \theta)^2], $$
记为$Mse(\hat{\theta})$. 若$\hat{\theta}$是$\theta$的无偏估计,则有$Mse(\hat{\theta}) = D(\hat{\theta})$.
均方误差作为$\hat{\theta}$误差大小从整体角度的一个衡量,这个量越小,就表示$\hat{\theta}$的误差平均来说比较小,因而也就越优. 由定义可以看出来,均方误差小并不能保证$\hat{\theta}$在每次使用时一定给出小的误差,它有时也可以有较大的误差,但这种情况出现的机会比较少.
一个例子:
用100个学生的平均成绩作为全校学生平均成绩的估计,比起用抽出的第一个学生的成绩去估计,哪种方法更好?设总体服从正态分布,这两个估计分别是$\bar{X} = (X_1 + ... + X_{100})/100$和$X_1$,如果我们分别计算这两个估计量的均方误差,可得
$$E[(\bar{X} - \mu)^2] = \sigma^2/100, E[(X_1 - \mu)^2] = \sigma^2$$
故$X_1$的均方误差是$\bar{X}$的100倍(如果多次随机取样每次取100个学生,那么$X_1$可能是任意一位学生,相当于随机变量$X$;$\bar{X}$也可能是任意100位同学,相当于$\bar{X}$。比较可以发现,此时求$Mse(\bar{X})$以及$Mse(X_1)$的公式其实就是求$X$和$\bar{X}$的方差的定义)。
1.4 相合性
相合性准则是根据“依概率收敛”的形式来定义的。这个形式与大数定律的形式相同,因此也可以用“相合性”从估计的观点来对大数定律作出解释。
定义:设$\hat{\theta}(X_1, ..., X_n)$为参数$\theta$的估计量,若对于任意$\theta$,当$n \to +\infty$时,
$\hat{\theta}_n \to \theta \ with \ probability \ p$,即$\forall \varepsilon \gt 0$, 有$\displaystyle \lim_{ n \to \infty } P(|\hat{\theta}_n - \theta| \geq \varepsilon) = 0 \quad \ldots $(1.4-1)
成立. 则称$\hat{\theta}_n$为$\theta$的相合估计量或一致估计量。
对于样本均值来说,大数定律指出当样本量足够大时,样本均值依概率趋近于总体均值,就相当于这里的估计量$\hat{\theta}$依概率趋近于待估计参数$\theta$。也就是说,概率$P(|\hat{\theta}_n - \theta| \geq \varepsilon)$表示的是“当样本大小为n时,样本均值$\bar{X}_n$这个估计值与真值$\theta$的偏离达到$\varepsilon$这么大或更大”的可能性。式子1.4-1表明:随着n的增加,这种可能性越来越小,以致趋于0.
1.5 相合性与渐进无偏性有什么区别?
这两个定义看起来差不多,很容易混淆。从形式上来看,渐进无偏性要求的是随着样本量的增加,估计量的期望趋近于被估计量;而相合性要求的是估计量本身趋近于被估计量。
如果估计量是收敛的,那么这两个定义几乎是等同的。但是如果估计量是不收敛的,例如始终是${-1, 1}$这两个数无限循环的数列,则被估计量的值恰好为0,这时候满足了渐进无偏性的条件,但是并不满足相合性的条件。因此可以说相合性比渐进无偏性的条件更加严格。满足了相合性就有极大的可能(因为相合性是依概率收敛,因此也不能说绝对满足)是满足渐进无偏性的,但是反过来却不一定。
2. 再谈统计量与枢轴量
概括的说,统计量本身完全是样本的函数,自身不包含任何未知参数(样本一旦确定,统计量的值也就定下来了),但是其分布却往往包含未知参数;枢轴量恰恰相反,枢轴量本身就包含总体中的未知参数,但是其分布的形式一般是确定的,不包含未知参数。
2.1 统计量
前面的小结中已经多次提到了统计量:小结7中对统计量做了基本说明,并且列出了常用的统计量,这些统计量可以用来对总体中的未知参数进行点估计(例如用样本均值估计总体均值);小结8中提到的三大抽样分布都是统计量的分布,这些统计量都是相互独立且服从标准正态分布的随机变量的函数(例如n个上述随机变量的平方和服从自由度为n的卡方分布)。
由上面的内容,可以得到统计量的一些特点:
- 统计量可以用于对总体中的未知参数进行点估计;
- 有些统计量的分布是明确的,例如“三大统计分布”所代表的统计量;
“三大抽样分布”都是统计量的分布,这些统计量的分布形式是明确的(有具体的数学公式,不包含未知参数),这也是为什么这三类分布在统计学中如此重要的原因之一。因为事实上大部分的统计量要么很难确定其分布,要么含有未知参数。
除此之外,统计量还有以下特点(参考wiki):
- 可观察性:事实上也就是说统计量不含有未知参数,一旦观察的样本确定了,统计量的值也就确定了(例如样本均值、样本方差、样本矩等);
- 便捷性:也就是具有某种概括性,只用一个量就描述了大量样本的某些重要特性(例如样本均值);
- 统计特性:完整性、一致性等;
- 分布已知且用于假设检验的统计量(例如三大分布所表示的统计量)也被称为检验统计量。
2.2 统计量 vs 总体参数
如果一个总体中的参数未知,例如全国人口的平均身高$\mu$,一般受限于时间或是人力物力我们不可能测量整个总体来确定这个参数的准确值。通常的做法是随机抽取一定量的样本(例如每个省抽取总人口的1%),然后求这些样本的平均身高(一个统计量),最后利用该统计量来估计总体中的未知参数。下面是wiki中的一个例子:
一个统计参数用于计算北美所有 25 岁的男性人口的平均身高。作为采样,我们随机地选择了 100 名符合条件的人测量了身高;这 100 人的平均身高是比较容易被统计出来的,而全部符合条件的人的平均身高是很难统计的,除非把每个人都拿来测量一遍身高。当然,如果普查了所有人,那么计算得到的数据则是统计参数(总体参数),而非统计量。
2.3 枢轴量
定义:设总体$X$有概率密度(或分布律)$f(x; \theta)$,其中$\theta$是待估的未知参数。设$X_1, ..., X_n$是一个样本,记:
$$G = G(X_1, ..., X_n; \theta)$$
为样本和待估参数$\theta$的函数,如果$G$的分布已知,不依赖与任何参数,就称$G$为枢轴量。
由上述定义可以看出枢轴量的几个特点:
- 与某个待估参数有关(事实上枢轴量法主要被用于未知参数的区间估计);
- 本身含有未知参数(待估参数),因此不具有“可观察性”,也就是说即使选定了样本也无法计算出确定的值;
- 其分布是明确的(有具体的数学公式,不包含未知参数)。
一个比较常见的例子:均值或方差未知的正态分布转换成标准正态分布时,随机变量中还是包含未知参数,但是其分布中却不包含任何未知参数。因此标准化之后的随机变量是一个枢轴量。
一般正态分布与标准正态分布之间的关系: 当$X \sim N(\mu, \sigma)$时,$\frac{X - \mu}{\sigma} \sim N(0, 1)$. 参考小结4中,“正态分布”部分的性质。
2.4 统计量 vs 枢轴量
再次比较一下这两个量的异同:
- 枢轴量和统计量都是样本的函数,但是枢轴量中还包含未知参数(待估计参数);
- 枢轴量和统计量的分布都是某种抽样分布,与样本本身所属的总体分布不同;
- 枢轴量的分布不依赖于任何未知参数,统计量的分布常依赖于未知参数;
- 如果将枢轴量中的未知参数用某个已知的估计量替代,那么枢轴量就变成统计量了;
- 统计量常用于点估计和假设检验;
- 枢轴量常用于区间估计。
问题:
总体$X \sim N(\mu, \sigma^2)$,$\mu, \sigma$是未知参数. 要估计参数$\mu$. 设$X_1, ..., X_n$是一样本,请问下面三个量,
$$\bar{X}, \frac{\bar{X} - \mu}{\sigma/\sqrt{ n } }, \frac{\bar{X} - \mu}{S/\sqrt{ n } }$$
哪些是统计量?哪些是枢轴量?
答:
(1) 只有$\bar{X}$是统计量,另两个含有未知参数,所以不是统计量;
(2) $\bar{X} \sim N(\mu, \sigma^2/n)$,分布含有未知参数;
(3) 第二项中除了$\mu$之外,还含有其他未知参数$\sigma$(不是枢轴量);
(4) 第三项只是$\mu$和样本的函数,服从$t(n - 1)$分布(是枢轴量)。
从这个例子可以看出来,我们之前熟知的样本均值$\bar{X}$是一个统计量,但是它的分布是不明确的(含有未知参数);第三项是一个枢轴量,本身含有未知参数,但是分布是明确的。
欢迎阅读“概率论与数理统计及Python实现”系列文章
Reference
https://zh.wikipedia.org/wiki/%E7%BB%9F%E8%AE%A1%E9%87%8F
http://blog.sciencenet.cn/blog-659252-924520.html
中国大学MOOC:浙江大学&哈工大,概率论与数理统计
《概率论与数理统计》,陈希孺,中国科学技术大学出版社


 浙公网安备 33010602011771号
浙公网安备 33010602011771号