【概率论与数理统计】小结6 - 大数定理与中心极限定理

注：这两个定理可以说是概率论中最重要的两个定理。也是由于中心极限定理的存在，使得正态分布从其他众多分布中脱颖而出，成为应用最为广泛的分布。这两个定理在概率论的历史上非常重要，因此对于它们的研究也横跨了几个世纪（始于18世纪初），众多耳熟能详的大数学家都对这两个定理有自己的贡献。因此，这两个定理都不是单一的定理。不同的大数定理和中心极限定理从不同的方面对相同的问题进行了阐述，它们条件各不相同，得到的结论的强弱程度也不一样。

 

1. 大数定理（law of large numbers，LLN）

---

图1-1，伯努利（1655-1705）

大数定律可以说是整个数理统计学的一块基石，最早的大数定律由伯努利在他的著作《推测术》中提出并给出了证明。这本书出版于伯努利去世后的1713年。数理统计学中包含两类重要的问题——对概率p的检验与估计。大数定律的本质是一类极限定理，它是由概率的统计定义“频率收敛于概率”引申而来的。简单来说就是n个独立同分布的随机变量的观察值的均值$\bar{X}$依概率收敛于这些随机变量所属分布的理论均值，也就是总体均值。

 

举一个古典概率模型的例子：拿一个盒子，里面装有大小、质地一样的球a+b个，其中白球a个，黑球b个。这时随机地从盒子中抽出一球(意指各球有同等可能被抽出)，则“抽出的球为白球”这一事件A的概率p=a/(a+b).但是如果不知道a、b的比值，则p也不知道。但我们可以反复从此盒子中抽球(每次抽出记下其颜色后再放回盒子中)。设抽了N次，发现白球出现了m次，则用m/N去估计p。这个估计含有其程度不确定的误差，但我们直观上会觉得，抽取次数N越大，误差一般会缩小。

 

从实用的角度看，概率的统计定义无非是一种通过实验去估计事件概率的方法。大数定律为这种后验地认识世界的方式提供了坚实的理论基础。正如伯努利在结束《推测术》时就其结果的意义作的表述：“如果我们能把一切事件永恒地观察下去，则我们终将发现：世间的一切事物都受到因果律的支配，而我们也注定会在种种极其纷纭杂乱的现象中认识到某种必然。”

 

1.1 定义

设$X_1, X_2, ..., X_n$是独立同分布的随机变量，记它们的公共均值为$\mu$。又设它们的方差存在并记为$\sigma^2$。则对任意给定的$\varepsilon > 0$，有

$$\displaystyle \lim_{ n \to \infty } P(| \bar{X}_n - \mu| \geq \varepsilon) = 0 \hspace{ 10pt } \ldots (1-1)$$

这个式子指出了“当n很大时，$\bar{X}_n$接近$\mu$”的确切含义。这里的“接近”是概率上的，也就是说虽然概率非常小，但还是有一定的概率出现意外情况（例如上面的式子中概率大于$\varepsilon$）。只是这样的可能性越来越小，这样的收敛性，在概率论中叫做“$\bar{X}_n$依概率收敛于$\mu$”。

 

1.2 Python模拟抛硬币

下面用程序模拟抛硬币的过程来辅助说明大数定律：

用random模块生成区间[0,1)之间的随机数，如果生成的数小于0.5，就记为硬币正面朝上，否则记为硬币反面朝上。由于random.random()生成的数可以看做是服从区间[0,1)上的均匀分布，所以以0.5为界限，随机生成的数中大于0.5或小于0.5的概率应该是相同的(相当于硬币是均匀的)。这样就用随机数模拟出了实际的抛硬币试验。理论上试验次数越多(即抛硬币的次数越多)，正反面出现的次数之比越接近于1(也就是说正反面各占一半).

 

import random
import matplotlib.pyplot as plt


def flip_plot(minExp, maxExp):
    """
    Assumes minExp and maxExp positive integers; minExp < maxExp
    Plots results of 2**minExp to 2**maxExp coin flips
    """
    # 两个参数的含义，抛硬币的次数为2的minExp次方到2的maxExp次方，也就是一共做了(2**maxExp - 2**minExp)批次实验，每批次重复抛硬币2**n次

    ratios = []
    xAxis = []
    for exp in range(minExp, maxExp + 1):
        xAxis.append(2**exp)
    for numFlips in xAxis:
        numHeads = 0 # 初始化，硬币正面朝上的计数为0
        for n in range(numFlips):
            if random.random() < 0.5:  # random.random()从[0, 1)随机的取出一个数
                numHeads += 1  # 当随机取出的数小于0.5时，正面朝上的计数加1
        numTails = numFlips - numHeads  # 得到本次试验中反面朝上的次数
        ratios.append(numHeads/float(numTails))  #正反面计数的比值
    plt.title('Heads/Tails Ratios')
    plt.xlabel('Number of Flips')
    plt.ylabel('Heads/Tails')
    plt.plot(xAxis, ratios)
    plt.hlines(1, 0, xAxis[-1], linestyles='dashed', colors='r')
    plt.show()

flip_plot(4, 16)

 

结果：

 

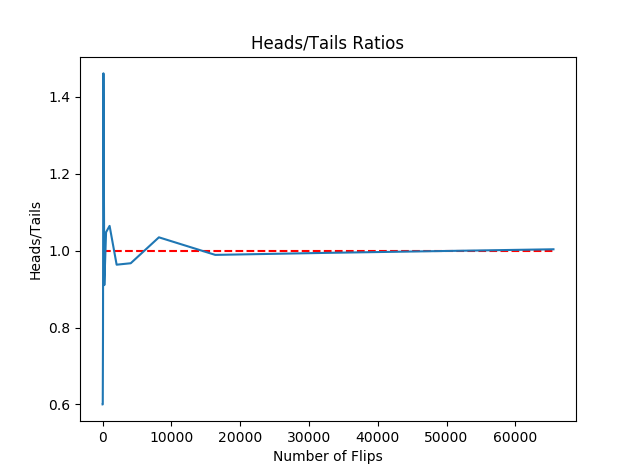
图1-2，随着实验次数的增加，正反面出现次数之比越来越接近于1

 

2. 中心极限定理（central limit theorem，CLT）

---

与大数定理描述某个值的收敛趋势不同，中心极限定理描述的是某种形式的随机变量之和的分布。

 

2.1 从大数定理到中心极限定理

2.1.1 对于这两个定理之间的联系与区别，知乎上的Detian Deng有如下回答：

简单来说，大数定律（LLN）和中心极限定理（CLT）的联系与区别在于：

共同点：都是用来描述独立同分布（i.i.d）的随机变量的和的渐进表现（asymptotic behavior)

区别：首先，它们描述的是在不同的收敛速率（convergence rate）之下的表现，其次LLN前提条件弱一点：$E(|X|) < \infty$ , CLT成立条件强一点：$E(X^2) < \infty$

上面的描述中，$E(X^2) < \infty$相当于表示随机变量$X$的二阶原点矩存在，即方差存在；$E(|X|) < \infty$表示$X$的一阶原点矩存在，即期望存在。方差存在可以推出期望存在，但是反之则不行。

 

2.1.2 我自己的理解：

利用大数定理我们可以用样本均值估计总体分布的均值。例如抛硬币，假如我们有一枚不均匀的硬币，事先并不知道正面朝上的概率$P_h$。那么我们可以大量重复抛这枚硬币，统计正面朝上的次数，用这个值除以抛硬币的总次数，就可以近似的得到一个比值，例如$P_1$。这个值就是对$P_h$的估计，根据大数定理，我们可以保证抛硬币的总次数越多这个估计的误差就越小（即$P_1$依概率收敛于$P_h$）。对于大数定理，故事到这里就结束了。

此时，如果我们将每次抛硬币都看成是一次伯努利试验，即$X \sim B(1, P_h)$，其中正面朝上记为1，概率为$P_h$。由于是同一个人进行的试验，可以将每次试验都看作是独立同分布。对于充分大的n，根据中心极限定理可得：

$$X_1 + X_2 + \cdots + X_n \sim N(nP_h, nP_h(1-P_h)) \hspace{ 10pt } \ldots (2-1)$$

上式表示所有试验结果之和，也就是硬币正面朝上的总次数，服从均值为$nP_h$，方差为$nP_h(1-P_h)$的正态分布。这里的分布是近似分布。严格意义上来说，n次伯努利试验之和服从二项分布$B(n, P_h)$，近似的正态分布中的均值和方差与对应的二项分布相同。式2-1是利用正态分布近似估计二项分布的理论基础（在$n$很大的前提下：$p$固定，$np$也很大时常用正态分布逼近；当$p$很小，$np$不太大时常用泊松分布逼近）。该式也是历史上最早的中心极限定理的表述形式。1716年棣莫弗讨论了p=1/2的情况，后来拉普拉斯将其推广到了一般p的情形。因此式2-1又叫做棣莫弗-拉普拉斯中心极限定理。

到这里，故事还没有结束。

假如此时又来了一个人，他不相信前一个人的试验结果，自己重新做了一次试验：大量的重复抛这枚硬币，他的估计值是$P_2$。接着又来了第三个人，第四个人，...，这些人每个人都做了一次这样的试验，每个人都得到了一个估计值$P_i$。那么这些不同的估计值之间有什么联系呢？类似上面一个人抛硬币的过程，如果将每个人抛硬币的试验看做是二项分布$B(n, P_h)$，正面记为1，背面记为0。那么每个人的试验结果之和都相当于一个具体的观察值，表示其试验中硬币正面朝上的总次数$X$。正面朝上的概率可以用$X/n$来估计。

由大数定理可得$X - n*P_h$依概率收敛于0（也就是说如果每个人的重复次数都非常多的话，每个人的结果都是依概率收敛于二项分布的期望），中心极限定理进一步给出了下面的结论：

值得注意的一点是，此时需要区分两个不同的量：一个是每个人重复伯努利试验的次数，还是取为$n$；另一个是参与试验的人数，这里取为$m$。

$$X_1 + X_2 + \cdots + X_m \sim N(\mu, \sigma^2) \hspace{ 10pt } \ldots (2-2)$$

也就是说，这m个不同的人的试验结果之和也是属于正态分布的。由于每个人的试验都相当于是一个二项分布，假如将每个二项分布都用式2-1逼近，那么这里的和就相当于服从式子2-1中正态分布的随机变量之和（这些不同的随机变量之间相互独立），也就不难求出这里的均值和方差分别为：$\mu = mnP_h, \sigma^2 = mnP_h(1-P_h)$。由于这些随机变量之间是相互独立的，因此求和以后均值和方差都扩大了m倍。

此外，

$$\bar{X} \sim N(nP_h, nP_h(1-P_h)/m) \hspace{ 10pt } \ldots (2-3)$$

其中，$\bar{X} = \frac{1}{m} \displaystyle \sum_{i=1}^{m}X_i$。同样本均值的均值和方差，m个人的结果均值的均值没变，方差缩小了m倍。

这里还有一个很好的问题是，m取多少比较合适。如果只取1，上面三个式子都是等价的，随着人数的增加，式2-3的方差越来越小，也就是说用多人的均值来估计的结果也越来越准确（不确定性减小了），而式2-2的方差会越来越大（所有人的试验结果之和）。对于式2-2，和式中的每一项都是一个二项分布，而不是式2-1中的伯努利分布。

那么和式中的每一项可以是其他分布吗？其实和式中的每一项可以是任意分布，只要每一项都是独立同分布且该分布的方差存在，那么当$m$趋近于无穷大时，它们的和就服从正态分布：

$$X_1 + X_2 + \cdots + X_m \sim N(m\mu, m\sigma^2) \hspace{ 10pt } \ldots (2-4)$$

其中$\mu$与$\sigma$是和式中每一项所属分布的期望和标准差。 式2-4是2-1的进一步推广，条件更弱，适用范围更加广泛。这就是独立同分布下的中心极限定理也叫作林德伯格-莱维（Lindeberg-Levi中心极限定理）。这里的服从也是近似服从。

 

2.2 用Python程序模拟中心极限定理

2.2.1 模拟服从伯努利分布的随机变量之和

这就相当于一个人做抛硬币的试验（正面朝上为1，反面朝上为0），这些试验结果之和就表示这个人的试验中出现正面朝上的总次数。

设单次伯努利试验服从$B(1, p)$，单次试验抛硬币n次（这n次试验结果合起来为该试验条件下的一个样本），重复单次试验$t$次（同下面代码中的$t$，$t$一般取值比较大），那么这些试验结果之和近似服从$N(np, np(1-p))$。其中$np$表示均值$\mu$，$np(1-p)$表示方差$\sigma^2$。

 

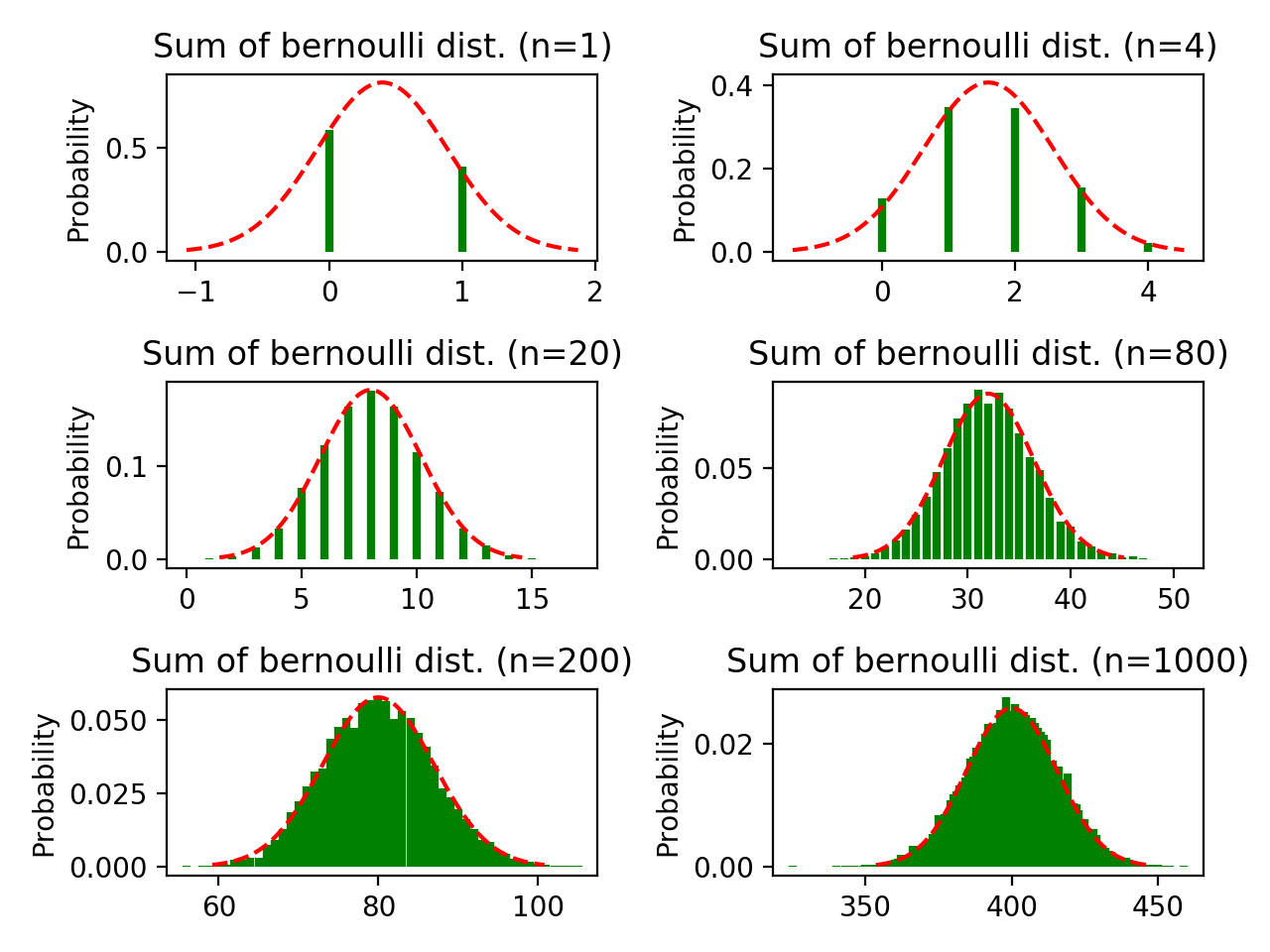
图2-1，n依次等于1, 4, 20, 80, 200, 1000；p等于0.4的伯努利分布之和

上图红色曲线表示用于逼近"多个取自伯努利分布的随机变量之和"的正态分布的概率密度曲线。由上图可以看到，当n（单次试验抛硬币的次数）等于20的时候，随机变量和的分布和对应的近似正态分布的形状已经高度重合。但是当n继续增大时，拟合程度反而有所下降，这是由于试验次数（下面代码中，函数sampling2pmf的参数t，相当于总的试验次数）和在x轴上分割的区间数（代码中第49行的bins）太小造成的。

t的大小就是最终"随机变量之和"这个新随机变量的取样个数（因此总共抛硬币$t*n$次）。

当n=1时，该随机变量就是伯努利分布本身，这时只有两个可能的取值：0和1，因此1出现了$tp$次，0出现了$t(1-p)$次。

当n=20时，该随机变量是20个服从伯努利分布的随机变量之和。这时的可能取值为[0, 20]的整数。0就表示这20次试验全都背面朝上，20就表示这20次试验全都正面朝上。每次试验都可以得到一个位于区间[0, 20]的整数，试验结束后，最终得到了t个这样的整数，这些整数的直方图的形状也近似为正态分布的形状。

下面是代码：

# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

"""
Created on Sun Nov 12 08:44:37 2017

@author: Belter
"""


def sampling2pmf(n, dist, t=10000):
    """
    n: sample size for each experiment
    t: how many times do you do experiment, fix in 10000
    dist: frozen distribution
    """
    ber_dist = dist
    sum_of_samples = []
    for i in range(t):
        samples = ber_dist.rvs(size=n)  # 与每次取一个值，取n次效果相同
        sum_of_samples.append(np.sum(samples))
    val, cnt = np.unique(sum_of_samples, return_counts=True)
    pmf = cnt / len(sum_of_samples)
    return val, pmf


def plot(n, dist, subplot, plt_handle):
    """
    :param n: sample size
    :param dist: distribution of each single sample
    :param subplot: location of sub-graph, such as 221, 222, 223, 224
    :param plt_handle: plt object
    :return: plt object
    """
    bins = 10000
    plt = plt_handle
    plt.subplot(subplot)
    mu = n * dist.mean()
    sigma = np.sqrt(n * dist.var())
    samples = sampling2pmf(n=n, dist=dist)
    plt.vlines(samples[0], 0, samples[1],
               colors='g', linestyles='-', lw=3)
    plt.ylabel('Probability')
    plt.title('Sum of bernoulli dist. (n={})'.format(n))
    # normal distribution
    norm_dis = stats.norm(mu, sigma)
    norm_x = np.linspace(mu - 3 * sigma, mu + 3 * sigma, bins)
    pdf1 = norm_dis.pdf(norm_x)
    plt.plot(norm_x, pdf1, 'r--')
    return plt

size = [1, 4, 20, 80, 200, 1000]

# sum of bernoulli distribution
dist_type = 'bern'
bern_para = [0.4]
single_sample_dist = stats.bernoulli(p=bern_para[0])  # 定义一个伯努利分布

# 下面是利用matplotlib画图
plt.figure(1)
plt = plot(n=size[0], dist=single_sample_dist, subplot=321, plt_handle=plt)
plt = plot(n=size[1], dist=single_sample_dist, subplot=322, plt_handle=plt)
plt = plot(n=size[2], dist=single_sample_dist, subplot=323, plt_handle=plt)
plt = plot(n=size[3], dist=single_sample_dist, subplot=324, plt_handle=plt)
plt = plot(n=size[4], dist=single_sample_dist, subplot=325, plt_handle=plt)
plt = plot(n=size[5], dist=single_sample_dist, subplot=326, plt_handle=plt)
plt.tight_layout()
plt.savefig('sum_of_{}_dist.png'.format(dist_type), dpi=200)

 

将上面代码中第13行的t和37行的bins都从10,000增加到1,000,000，可以得到下图：

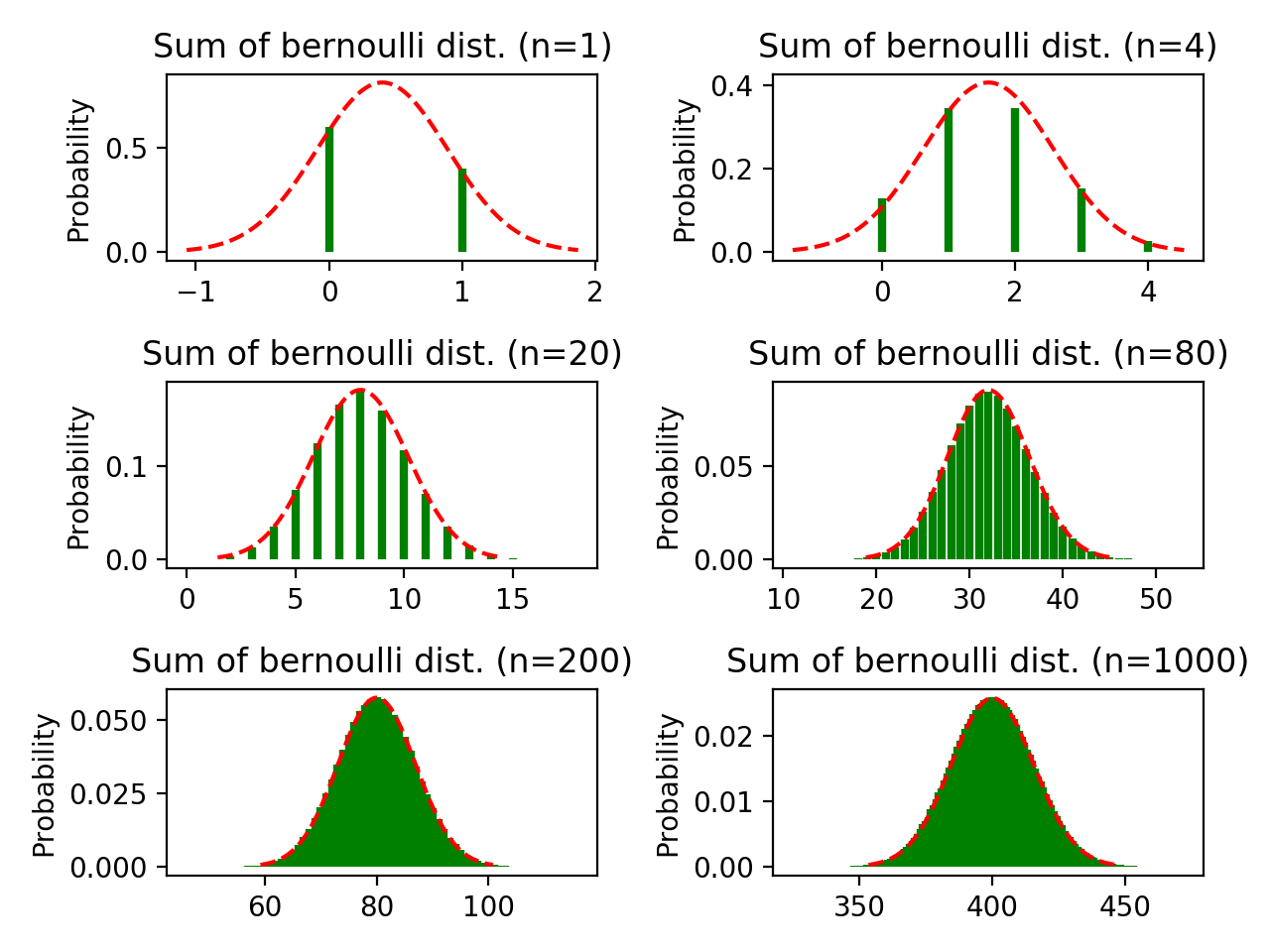
 图2-2，增加试验次数和在x轴上的分割区间，其他参数同2-1

由上图可以看到，增加试验次数和在x轴上分割区间的个数后，随机变量之和与正态分布之间的重合度随着样本量（在代码的54行定义）的增加而升高。这也很容易解释：对于随机变量和的分布，抽样次数（试验次数）越多，最终画出来的图越能代表整个分布，但是抽样次数本身却不影响该分布的类型和参数。就像在学校研究全体同学的身高，抽样的人数不会影响身高的真实分布，只会影响我们利用所得的样本描绘出来的分布的形状。

此外，还有一个因素对随机变量和的分布也有极大的影响：单次试验所在分布的参数，这里是指伯努利分布中的参数$p$，下面是将$p$从$0.4$增加到$0.99$后的图形：

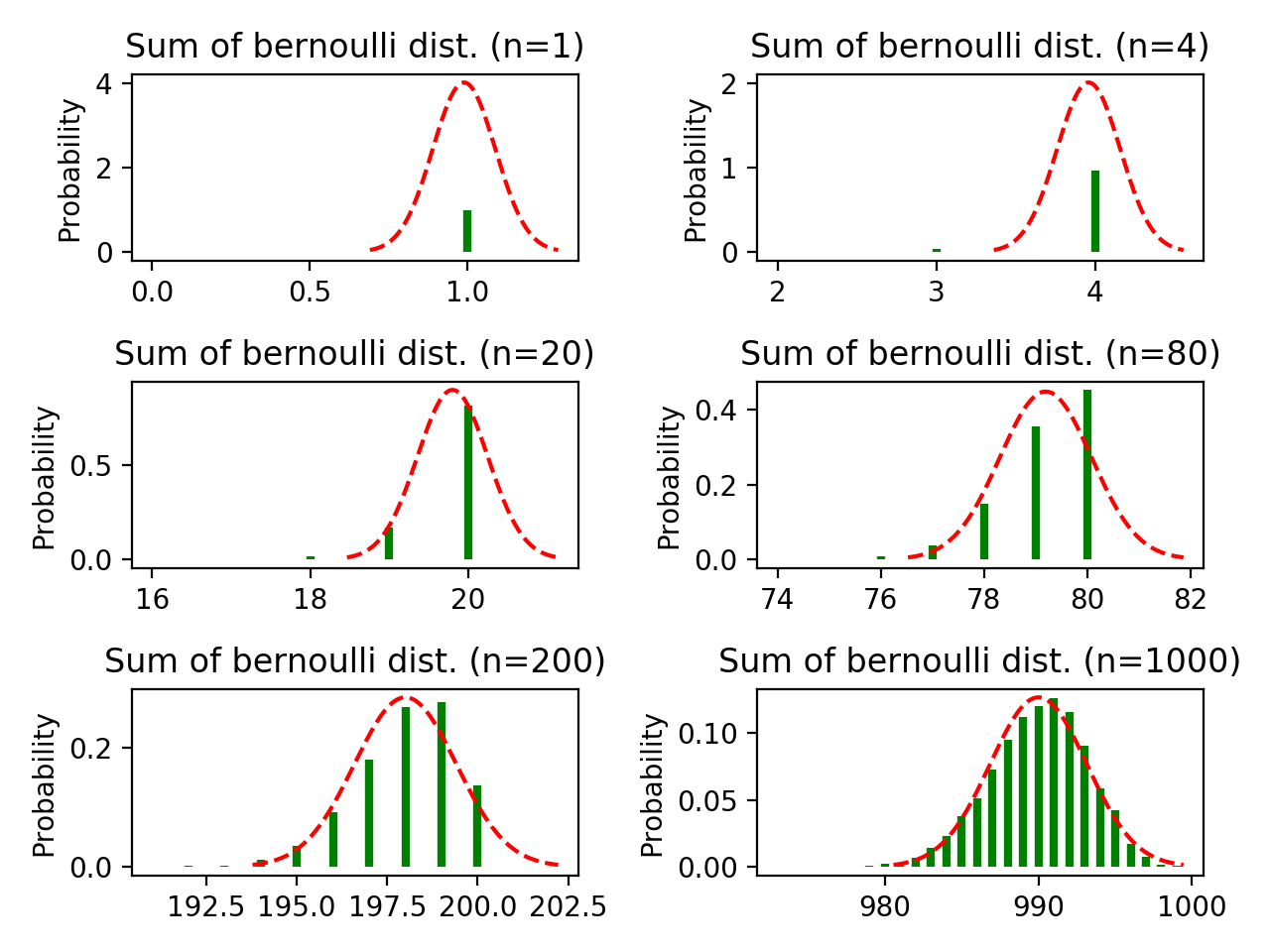
 图2-3，n依次等于1, 4, 20, 80, 200, 1000；p等于0.99的伯努利分布之和

 由上图可以看到，由于单个样本所在的伯努利分布严重不均匀（如果这个试验表示抛硬币且正面朝上记为1，那就意味着99%的情况下都只出现正面），导致后面随机变量之和的图形都出现了偏斜。但是，偏斜程度随着样本量的增加而降低。如果样本量继续增加，就会基本消除这种偏斜。

 

2.2.2 模拟服从二项分布的随机变量之和

这就相当于多个人做抛硬币的试验（正反面朝上还是分别记为1和0），这些试验结果之和就表示所有人的试验中出现正面朝上的总次数。

设单次二项试验服从$B(m, p)$，参与人数为n，那么这些试验结果之和近似服从$N(nmp, nmp(1-p))$。其中$nmp$表示均值$\mu$，$nmp(1-p)$表示方差$\sigma^2$。

只需要将上面代码中的57-59行替换成下面的代码就可以模拟出二项分布之和的情况：

...
dist_type = 'bino'
bino_para = [20, 0.4]
single_sample_dist = stats.binom(n=bino_para[0], p=bino_para[1])  # 定义一个二项分布
...

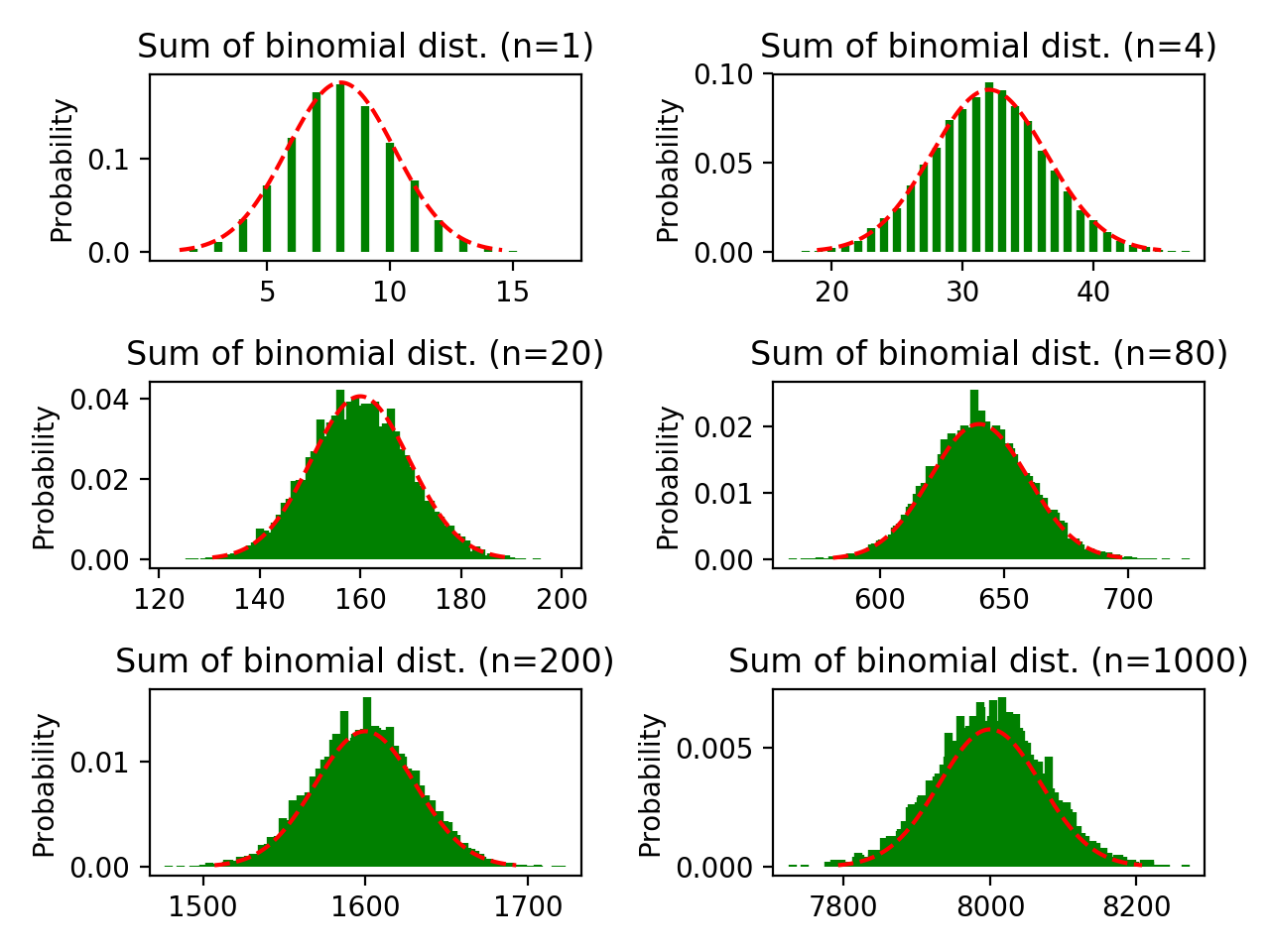
图2-4，n依次等于1, 4, 20, 80, 200, 1000；参数为(20, 0.4)的二项分布之和

图片中的n表示每次试验参加的人数，每个人做单次试验时，试验服从$B(20， 0.4)$。

当n=1时，就相当于图2-1中n=20的情况：都是一个人重复"抛20次硬币"这一试验，正面朝上的概率也相同。

当n=80时，就相当于有80个人同时做服从参数为(20, 0.4)的二项分布试验，这些人之间的试验是相互独立的，然后将这些人的实验结果相加：所以此时的均值为80*20*0.4=640，标准差为$\sqrt{80*20*0.4*(1-0.4)} \approx 19.6$，且最大值为80*20=1600（相当于所有人的试验结果全部都是1），最小值为0（相当于所有人的试验结果都是0）。

宏观解释：当非常多的人一起重复结果服从上述二项分布的试验时，每次抛硬币最可能得到正面朝上的概率始终都是$p$，因此这些人完成一次试验的结果之和的期望就是：人数 * 每人单次试验抛硬币数 * 硬币正面朝上的概率，即$n * 20 * 0.4$。得到硬币正面朝上的结果小于这个概率，会导致试验结果之和小于平均值；反之则会使试验结果之和大于平均值。但是这两种情况都没有以概率$p$出现更常见，因此就产生了取到均值的概率最大，越往两边概率越小的钟型概率密度曲线。

 

2.2.3 模拟服从均匀分布的随机变量之和

还是假设每次有n个人参与服从$U[a, b]$的均匀分布，则求和就相当于将这些人的试验结果相加，那么这些试验结果之和近似服从$N(\frac{n(b-a)}{2}, \frac{n(b-a)^2}{12})$。其中$\frac{n(b-a)}{2}$表示均值$\mu$，$\frac{n(b-a)^2}{12}$表示方差$\sigma^2$（近似正态分布的参数都是原均匀分布参数的n倍，参考式2-4）。

取参数为[3, 5]的均匀分布，可得：

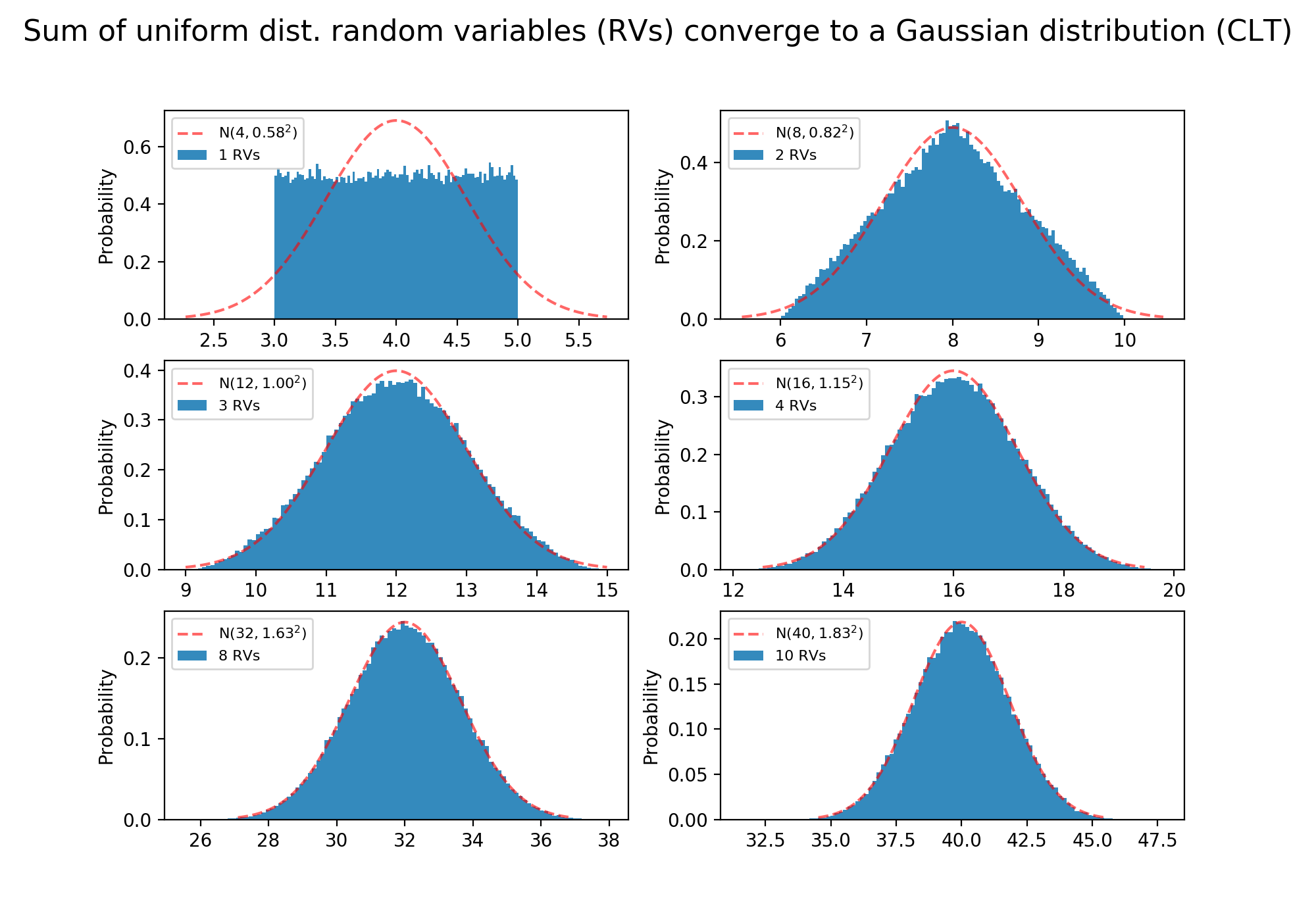
 图2-5，服从均匀分布$U[3, 5]$的随机变量之和

使用前面模拟离散型随机变量和的方法无法模拟连续型随机变量和的极限分布，这是因为连续型随机变量的取值是无穷多的，单个点的概率等于0，即使大量重复取样每个结果的概率都还是会非常小（因为每个值都不同），根本无法看到累积的效果。可以将x轴进行分区，将出现在同一个区域的观察值当做相同的值来对待，这样就跟离散型随机变量的情况一样了（将无穷多的可能取值转化成了有限个区域的取值）。下面使用hist函数实现了这一方式，并且将bins设置为100。

对于本次试验的均匀分布，每次取值为区间$[3, 5]$上的任意实数，且取到这些实数的概率是相等的。

当n=1时，相当于只有一个人进行服从该均匀分布的试验，试验次数为函数“sampling2pmf”中的参数“t”，即100000次。由于将区间$[3, 5]$等分为100份，因此这些观察值也应该均匀的分布在这100个区间内，即每个小区间中会有大约1000个观察值。由于总长度为2，此时整个矩形区域的面积为$1000*2 = 2000$，如果标准化为频率可得到每个小区间中观察值出现的频率为观察值个数除以总面积，即$1000/2000 = 0.5$。最终结果就得到了左上角的图形。此时相当于均值和方差都相同的正态分布（红色虚线）和均匀分布（蓝色区域）的比较，相差还是非常大的。

当n=8时，相当于有8个人同时做该试验，每次试验完成后将这些人的观察值相加，试验$t$次，就可以得到$t$个相加的观察值。由于每次试验从均匀分布中取值，这8个人的试验结果也应该大致服从均匀分布，这些值几乎均匀的分布在区间$[3, 5]$上。因此其和约等于人数乘以均匀分布的均值，即$8*4 = 32$，这也是n=8时，随机变量和的期望值。该期望值是这8个人的结果之和最有可能出现的值，因此概率最大；大于该值或小于该值的概率表示这些人的取值会偏向均值的右侧或左侧，因此概率会减小。

宏观解释：多人试验时，有些人取到较大的值，有些人取到较小的值，因此总的来说这些值的和接近人数乘以均匀分布的均值，得到这个位置的值的概率最大，为图形中的顶点。所有人的取值同时小于或大于均值的概率是比较小的，因此顶点两侧的概率降低了，且越往两侧概率越小。取到极小值（极大值）表示所有人都取到了均匀分布中的最小值3（最大值5），这几乎是不可能的。

下面是代码实现：

# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

"""
Created on Sun Nov 17 18:44:37 2017

@author: Belter
"""


def sampling2pmf(n, dist, t=100000):
    """
    n: sample size for each experiment
    t: how many times do you do experiment, fix in 100000
    dist: frozen distribution
    """
    current_dist = dist
    sum_of_samples = np.zeros(t)
    for i in range(t):
        samples = []
        for j in range(n):  # n次独立的试验
            samples.append(current_dist.rvs())
        sum_of_samples[i] = np.sum(samples)
    return sum_of_samples


def plot(n, dist, subplot):
    """
    :param n: sample size
    :param dist: distribution of each single sample
    :param subplot: location of sub-graph, such as 221, 222, 223, 224
    """
    plt.subplot(3, 2, subplot)
    mu = n * dist.mean()
    sigma = np.sqrt(n * dist.var())
    samples = sampling2pmf(n=n, dist=dist)
    # normed参数可以对直方图进行标准化，从而使纵坐标表示概率而不是次数
    plt.hist(samples, normed=True, bins=100, color='#348ABD',
             label='{} RVs'.format(n))
    plt.ylabel('Probability')
    # normal distribution
    norm_dis = stats.norm(mu, sigma)
    norm_x = np.linspace(mu - 3 * sigma, mu + 3 * sigma, 10000)
    pdf = norm_dis.pdf(norm_x)
    plt.plot(norm_x, pdf, 'r--', alpha=0.6, label='N(${0:.0f}, {1:.2f}^2$)'.format(mu, sigma))
    plt.legend(loc='upper left', prop={'size': 8})

size = [1, 2, 3, 4, 8, 10]

# sum of uniform distribution
dist_type = 'uniform'
uniform_para = [3, 2]
single_sample_dist = stats.uniform(loc=uniform_para[0], scale=uniform_para[1])  # 定义一个均匀分布

# 下面是利用matplotlib画图
plt.figure(figsize=(10, 7))  # bigger size
plt.suptitle('Sum of {} dist. random variables (RVs) converge to a Gaussian distribution (CLT)'.format(dist_type),
             fontsize=16)
for s in range(len(size)):
    plot(n=size[s], dist=single_sample_dist, subplot=s+1)

plt.savefig('sum_of_{}_dist.png'.format(dist_type), dpi=200)

上面的代码参考了这里，整体上也更加简洁。

 

后记：

写到这里，似乎任何分布之和（只要项数足够多）都服从正态分布。但是就是在上面链接的末尾处看到了一个例外：任意多的服从柯西分布的随机变量之和还是服从原来的柯西分布。后面查了一些资料证实了这一点，可以参考这里。有了这一个例外，可能就无法排除还有其他的例外，只是这种情况应该很少见，平时的数据分析中也很少会遇到服从柯西分布的数据（物理学除外）。因此也不用担心中心极限定理突然失灵。大数定理部分，写于大约两年前，当时发布在新浪博客（reference中最后一个链接），转载时做了一些小的修改。

 

欢迎阅读“概率论与数理统计及Python实现”系列文章

 

Reference

---

http://skhdh.blog.163.com/blog/static/279661392013126402728/

https://www.zhihu.com/question/22913867

https://www.zhihu.com/question/22913867/answer/35058403

https://www.quora.com/What-is-the-difference-between-the-Weak-Law-of-Large-Numbers-and-the-Central-Limit-Theorem/answer/Michael-Hochster?srid=uIoGQ

https://math.stackexchange.com/questions/2521380/using-python-simulate-central-limit-theorem-bigger-n-worse-fitting

https://rajeshrinet.github.io/blog/2014/central-limit-theorem/

http://blog.sina.com.cn/s/blog_6a6c136d0102wvrc.html