【概率论与数理统计】小结4 - 一维连续型随机变量及其Python实现
注:上一小节总结了离散型随机变量,这个小节总结连续型随机变量。离散型随机变量的可能取值只有有限多个或是无限可数的(可以与自然数一一对应),连续型随机变量的可能取值则是一段连续的区域或是整个实数轴,是不可数的。最常见的一维连续型随机变量有三种:均匀分布,指数分布和正态分布。下面还是主要从概述、定义、主要用途和Python的实现几个方面逐一描述。
以下所有Python代码示例,均默认已经导入上面的这几个包,导入代码如下:
import numpy as np from scipy import stats import matplotlib.pyplot as plt
Python中调用一个分布函数以及相关方法还是遵循以下步骤:
- 初始化一个分布函数(也叫作冻结的分布);
- 调用该分布函数的方法或计算其数值特征;
1. 均匀分布
均匀分布算是最简单的连续型概率分布。因为其概率密度是一个常数,不随随机变量X取值的变化而变化。
1.1 定义
如果连续型随机变量 $X$ 具有如下的概率密度函数,则称 $X$ 服从 $[a,b]$ 上的均匀分布(uniform distribution),记作 $X \sim U(a,b)$ 或 $X \sim Unif(a,b)$
\begin{equation}
\nonumber f_X(x) = \left\{
\begin{array}{l l}
\frac{1}{b-a} & \quad a < x < b\\
0 & \quad x < a \textrm{ or } x > b
\end{array} \right.
\end{equation}
均匀分布具有等可能性,也就是说,服从 $U(a,b)$ 上的均匀分布的随机变量 $X$ 落入 $(a, b)$ 中的任意子区间上的概率只与其区间长度有关,与区间所处的位置无关。
由于均匀分布的概率密度函数是一个常数,因此其累积分布函数是一条直线,即随着取值在定义域内的增加,累积分布函数值均匀增加。
\begin{equation}
\hspace{70pt}
F_X(x) = \left\{
\begin{array}{l l}
0 & \quad \textrm{for } x < a \\
\frac{x-a}{b-a} & \quad \textrm{for }a \leq x \leq b\\
1 & \quad \textrm{for } x > b
\end{array} \right.
\hspace{70pt}
\end{equation}

图1-1,均匀分布的累积分布函数曲线
1.2 主要用途
- 设通过某站的汽车10分钟一辆,则乘客候车时间 $X$ 在 $[0, 10]$ 上服从均匀分布;
- 某电台每个20分钟发一个信号,我们随手打开收音机,等待时间 $X$ 在 $[0, 20]$ 上服从均匀分布;
- 随机投一根针与坐标纸上,它和坐标轴的夹角 $X$ 在 $[0, π]$ 上服从均匀分布。
1.3 Python实现
从定义可以看出来,定义一个均匀分布需要两个参数,定义域区间的起点 $a$ 和终点 $b$,但是在Python中是 location 和 scale, 分别表示起点和区间长度。
参考:https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.uniform.html#scipy.stats.uniform
1 def uniform_distribution(loc=0, scale=1): 2 """ 3 均匀分布,在实际的定义中有两个参数,分布定义域区间的起点和终点[a, b] 4 :param loc: 该分布的起点, 相当于a 5 :param scale: 区间长度, 相当于 b-a 6 :return: 7 """ 8 uniform_dis = stats.uniform(loc=loc, scale=scale) 9 x = np.linspace(uniform_dis.ppf(0.01), 10 uniform_dis.ppf(0.99), 100) 11 fig, ax = plt.subplots(1, 1) 12 13 # 直接传入参数 14 ax.plot(x, stats.uniform.pdf(x, loc=2, scale=4), 'r-', 15 lw=5, alpha=0.6, label='uniform pdf') 16 17 # 从冻结的均匀分布取值 18 ax.plot(x, uniform_dis.pdf(x), 'k-', 19 lw=2, label='frozen pdf') 20 21 # 计算ppf分别等于0.001, 0.5, 0.999时的x值 22 vals = uniform_dis.ppf([0.001, 0.5, 0.999]) 23 print(vals) # [ 2.004 4. 5.996] 24 25 # Check accuracy of cdf and ppf 26 print(np.allclose([0.001, 0.5, 0.999], uniform_dis.cdf(vals))) # Ture 27 28 r = uniform_dis.rvs(size=10000) 29 ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2) 30 plt.ylabel('Probability') 31 plt.title(r'PDF of Unif({}, {})'.format(loc, loc+scale)) 32 ax.legend(loc='best', frameon=False) 33 plt.show() 34 35 uniform_distribution(loc=2, scale=4)
上面的代码采用两种方式——直接传入参数和先冻结一个分布,画出来均匀分布的概率分布函数。此外还从该分布中取了10000个值做直方图。
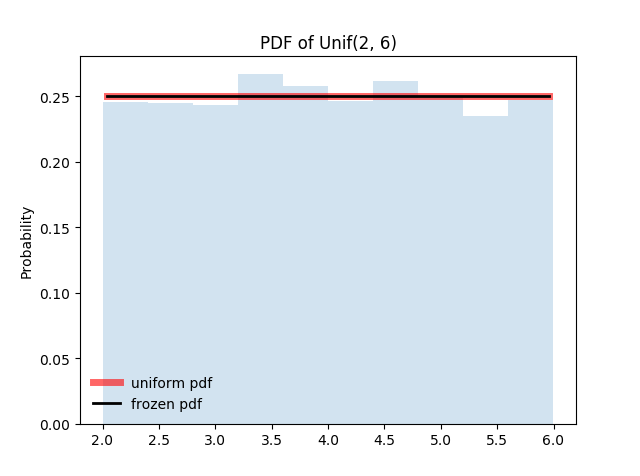
图2-2,均匀分布 $U(2, 6)$ 的概率密度函数曲线
2. 指数分布
其实指数分布和离散型的泊松分布之间有很大的关系。泊松分布表示单位时间(或单位面积)内随机事件的平均发生次数,指数分布则可以用来表示独立随机事件发生的时间间隔。由于发生次数只能是自然数,所以泊松分布自然就是离散型的随机变量;而时间间隔则可以是任意的实数,因此其定义域是 $(0, +\infty)$。
2.1 定义
如果一个随机变量 $X$ 的概率密度函数满足一下形式,就称 $X$ 为服从参数 $\lambda$ 的指数分布(Exponential Distribution),记做 $X \sim E(\lambda)$ 或 $X \sim Exp(\lambda)$.
指数分布只有一个参数 $\lambda$,且 $\lambda > 0$.
\begin{equation}
\nonumber f_X(x) = \left\{
\begin{array}{l l}
\lambda e^{-\lambda x} & \quad x > 0\\
0 & \quad \textrm{otherwise}
\end{array} \right.
\end{equation}
2.2 主要用途
- 表示独立随机事件发生的时间间隔,比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔等;
- 在排队论中,一个顾客接受服务的时间长短也可以用指数分布来近似;
- 无记忆性的现象(连续时间)。
2.3 性质
指数分布的一个显著的特点是其具有无记忆性。例如如果排队的顾客接受服务的时间长短服从指数分布,那么无论你已经排了多久时间的队,在排 t 分钟的概率始终是相同的。
用公式表示就是:
$$P(X \geq s + t | X \geq s) = P(X \geq t)$$.
其实我还没有找到一种直观的理解指数分布这一性质的方法。
2.4 Python 实现
这里的参数与实际指数分布的参数有点不一样,参考下面代码中的注释。
1 def exponential_dis(loc=0, scale=1.0): 2 """ 3 指数分布,exponential continuous random variable 4 按照定义,指数分布只有一个参数lambda,这里的scale = 1/lambda 5 :param loc: 定义域的左端点,相当于将整体分布沿x轴平移loc 6 :param scale: lambda的倒数,loc + scale表示该分布的均值,scale^2表示该分布的方差 7 :return: 8 """ 9 exp_dis = stats.expon(loc=loc, scale=scale) 10 x = np.linspace(exp_dis.ppf(0.000001), 11 exp_dis.ppf(0.999999), 100) 12 fig, ax = plt.subplots(1, 1) 13 14 # 直接传入参数 15 ax.plot(x, stats.expon.pdf(x, loc=loc, scale=scale), 'r-', 16 lw=5, alpha=0.6, label='uniform pdf') 17 18 # 从冻结的均匀分布取值 19 ax.plot(x, exp_dis.pdf(x), 'k-', 20 lw=2, label='frozen pdf') 21 22 # 计算ppf分别等于0.001, 0.5, 0.999时的x值 23 vals = exp_dis.ppf([0.001, 0.5, 0.999]) 24 print(vals) # [ 2.004 4. 5.996] 25 26 # Check accuracy of cdf and ppf 27 print(np.allclose([0.001, 0.5, 0.999], exp_dis.cdf(vals))) 28 29 r = exp_dis.rvs(size=10000) 30 ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2) 31 plt.ylabel('Probability') 32 plt.title(r'PDF of Exp(0.5)') 33 ax.legend(loc='best', frameon=False) 34 plt.show() 35 36 exponential_dis(loc=0, scale=2)
上面给出了 $Exp(0.5)$ 的概率分布函数图,

图2-1, $Exp(0.5)$ 的概率分布函数图
下面是对不同参数的指数分布的概率分布函数图的比较:

图2-2,不同参数的指数分布pdf图
代码如下:

1 def diff_exp_dis(): 2 """ 3 不同参数下的指数分布 4 :return: 5 """ 6 exp_dis_0_5 = stats.expon(scale=0.5) 7 exp_dis_1 = stats.expon(scale=1) 8 exp_dis_2 = stats.expon(scale=2) 9 10 x1 = np.linspace(exp_dis_0_5.ppf(0.001), exp_dis_0_5.ppf(0.9999), 100) 11 x2 = np.linspace(exp_dis_1.ppf(0.001), exp_dis_1.ppf(0.999), 100) 12 x3 = np.linspace(exp_dis_2.ppf(0.001), exp_dis_2.ppf(0.99), 100) 13 fig, ax = plt.subplots(1, 1) 14 ax.plot(x1, exp_dis_0_5.pdf(x1), 'b-', lw=2, label=r'lambda = 2') 15 ax.plot(x2, exp_dis_1.pdf(x2), 'g-', lw=2, label='lambda = 1') 16 ax.plot(x3, exp_dis_2.pdf(x3), 'r-', lw=2, label='lambda = 0.5') 17 plt.ylabel('Probability') 18 plt.title(r'PDF of Exponential Distribution') 19 ax.legend(loc='best', frameon=False) 20 plt.show() 21 22 diff_exp_dis()
3. 正态分布
正态分布也许是出现频率最高的分布,其他人对正态分布的熟悉程度应该也是所有分布中最高的。由于中心极限定理的存在,正态分布也是所有分布应用最广泛的分布,没有之一。
3.1 定义
若随机变量 X 的概率密度符合下面的形式,就称 X 服从参数为 $\mu, \sigma$ 的正态分布(或高斯分布),记为 $X \sim N(\mu,\sigma^2)$.
$$f_X (x) = \frac{1}{\sqrt{2 \pi } \sigma} \exp \left\{-\frac{(x - \mu)^2}{2 \sigma^2} \right\}, \hspace{20pt} \textrm{for all } x \in \mathbb{R}.$$
如果上面公式中 $\mu = 0, \sigma = 1$,就叫做标准正态分布,一般记做 $Z \sim N(0, 1)$。
由于标准正态分布在统计学中的重要地位,它的累积分布函数(CDF)有一个专门的表示符号:$\Phi$. 一般在统计相关的书籍附录中的“标准正态分布函数值表”就是该值与随机变量的取值之间的对于关系。
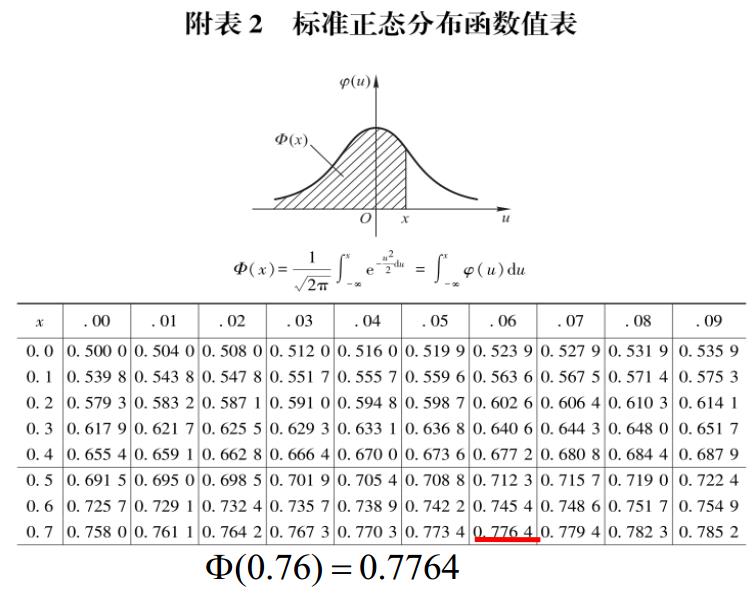
图3-1,标准正态分布的累计分布函数值表
正态分布中两个参数含义:
- 当固定 $\sigma$,改变 $\mu$ 的大小时,f(x) 图形的形状不变,只是沿着 x 轴作平移变换,因此 $\mu$ 被称为位置参数(决定对称轴的位置);
- 当固定 $\mu$,改变 $\sigma$ 的大小时, f(x) 图形的对称轴不变,形状改变, $\sigma$ 越小,图形越高越瘦, $\sigma$ 越大,图形越矮越胖,因此 $\sigma$ 被称为尺度参数(决定曲线的分散程度)
3.2 性质
- f(x) 关于 $x=\mu$ 对称;
- 当$x \leq \mu$时,f(x)是严格单调递增函数;
- $f_{max} = f(\mu) = \frac{1}{\sqrt{2 \pi } \sigma}$;
- 当 $X \sim N(\mu, \sigma^2)$ 时,$\frac{X - \mu}{\sigma} \sim N(0, 1)$
利用第4条性质,在计算一般正态分布的概率时,可以转化为标准正态分布函数来计算。
3.3 Python实现
pdf 和 cdf 图之前画过,这里就不重复了。

def normal_dis(miu=0, sigma=1): """ 正态分布有两个参数 :param miu: 均值 :param sigma: 标准差 :return: """ norm_dis = stats.norm(miu, sigma) # 利用相应的分布函数及参数,创建一个冻结的正态分布(frozen distribution) x = np.linspace(-5, 15, 101) # 在区间[-5, 15]上均匀的取101个点 # 计算该分布在x中个点的概率密度分布函数值(PDF) pdf = norm_dis.pdf(x) # 计算该分布在x中个点的累计分布函数值(CDF) cdf = norm_dis.cdf(x) # 下面是利用matplotlib画图 plt.figure(1) # plot pdf plt.subplot(211) # 两行一列,第一个子图 plt.plot(x, pdf, 'b-', label='pdf') plt.ylabel('Probability') plt.title(r'PDF/CDF of normal distribution') plt.text(-5.0, .12, r'$\mu={},\ \sigma={}$'.format(miu, sigma)) # 3是标准差,不是方差 plt.legend(loc='best', frameon=False) # plot cdf plt.subplot(212) plt.plot(x, cdf, 'r-', label='cdf') plt.ylabel('Probability') plt.legend(loc='best', frameon=False) plt.show() normal_dis(miu=5, sigma=3)
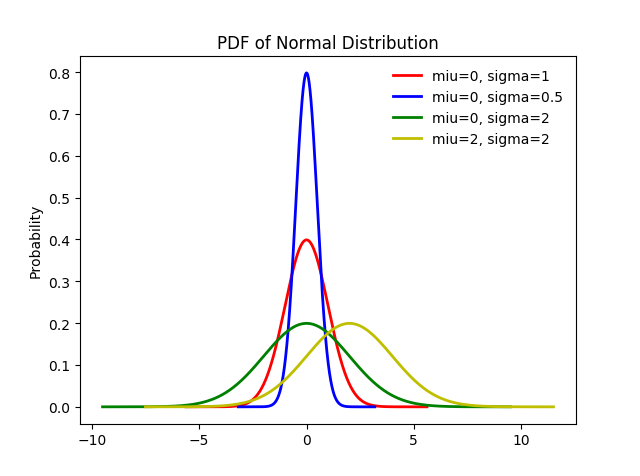
图3-2, 不同参数zhentfenbu正态分布的pdf图
代码如下:
1 def diff_normal_dis(): 2 """ 3 不同参数下的指数分布 4 :return: 5 """ 6 norm_dis_0 = stats.norm(0, 1) # 标准正态分布 7 norm_dis_1 = stats.norm(0, 0.5) 8 norm_dis_2 = stats.norm(0, 2) 9 norm_dis_3 = stats.norm(2, 2) 10 11 x0 = np.linspace(norm_dis_0.ppf(1e-8), norm_dis_0.ppf(0.99999999), 1000) 12 x1 = np.linspace(norm_dis_1.ppf(1e-10), norm_dis_1.ppf(0.9999999999), 1000) 13 x2 = np.linspace(norm_dis_2.ppf(1e-6), norm_dis_2.ppf(0.999999), 1000) 14 x3 = np.linspace(norm_dis_3.ppf(1e-6), norm_dis_3.ppf(0.999999), 1000) 15 fig, ax = plt.subplots(1, 1) 16 ax.plot(x0, norm_dis_0.pdf(x0), 'r-', lw=2, label=r'miu=0, sigma=1') 17 ax.plot(x1, norm_dis_1.pdf(x1), 'b-', lw=2, label=r'miu=0, sigma=0.5') 18 ax.plot(x2, norm_dis_2.pdf(x2), 'g-', lw=2, label=r'miu=0, sigma=2') 19 ax.plot(x3, norm_dis_3.pdf(x3), 'y-', lw=2, label=r'miu=2, sigma=2') 20 plt.ylabel('Probability') 21 plt.title(r'PDF of Normal Distribution') 22 ax.legend(loc='best', frameon=False) 23 plt.show() 24 25 diff_normal_dis()
4. 指数分布与泊松分布的关系
先总体上比较一下这两个分布:
- 在泊松分布中,时间是固定的(例如单位时间内),研究的随机变量 $X$ 是某事件在该时间段内出现的次数。其均值为 $\lambda$,表示某随机事件在单位时间内平均发生的次数;
- 在指数分布中,出现的次数是固定的(比如出现了1次),研究的是随机变量 $T$ 出现(发生,或到达)1次需要的时间。其均值为 $1/ \lambda$,表示某随机事件发生一次的平均时间间隔。
- $\lambda$ 越大,表示单位时间里发生的次数就越多,那么每两次事件之间的时间间隔$1/ \lambda$也就越小。
已知泊松分布在时间$t$上的PMF为(此时可以将$t$看做是一个固定的常数):
\begin{equation}
\nonumber P_X(k) = \left\{
\begin{array}{l l}
\frac{e^{-\lambda t} (\lambda t)^k}{k!}& \quad \text{for } k \in R_X\\
0 & \quad \text{ otherwise}
\end{array} \right. \hspace{ 10pt} \cdots (1)
\end{equation}
泊松过程中,第k次随机事件与第k+1次随机事件出现的时间间隔服从指数分布。而根据泊松过程的定义,我们定义 $T$ 为两次随机事件出现的时间间隔。此时 $T$ 是一个随机变量,并且可以得到 $T$ 的分布函数为:
$$ F(t) = Pr(T \leq t) \hspace{ 10pt} \cdots (2) $$
上式就等于,
$$ F(t) = Pr(T \leq t) = 1 - Pr(T > t) \hspace{ 10pt} \cdots (3) $$
在长度为 t 的时间段内没有随机事件出现的概率,即时间间隔大于$t$,(下面的式子是理解泊松分布与指数分布之间关系的关键!):
$$ Pr(T > t) = Pr(随机事件在时间 t 内出现了0次) = Pr(X = 0) = \frac {e^{-\lambda t}(\lambda t)^{0}}{0!} = e^{-\lambda t} \hspace{ 10pt} \cdots (4) $$
将上式带入 (3) 式就可以得到:
$$F(t) = 1 - e^{-\lambda t} \hspace{ 10pt} \cdots (5)$$
这个式子就是指数分布的累积分布函数,对 (5) 式求导后,就可以得到指数分布的概率密度函数,同定义中给出的形式。
举一个例子来更好的理解指数分布和泊松分布之间的关系:
这个例子来源于泊松分布的wiki主页,一条河平均100年会有一次洪水泛滥,那么如何来求时间小于某个时间点,会有洪水发生的概率?
根据题意可得,如果将100年作为一个单位时间,那么 $\lambda = 1$,即在单位时间内平均发生洪水泛滥的次数。
那么根据 (5) 式就可以计算出小于某个特定时间点,可能会发生洪水的概率。
下面是分别取 $\lambda$ 为1, 0.2和5得到的指数分布的 CDF 图。

图4-1, 取每一百年不同的洪水泛滥次数,得到的以洪水泛滥发生时间为随机变量的CDF图
上图可以理解为,如果每100年发生洪水的次数越多($\lambda$ 越大),那么下一次发生洪水的时间间隔越短。例如我们取时间为2.5, 表示第250年,则会预期在250年内发生洪水泛滥的概率:
- 蓝色线的概率取值几乎为1 ,表示如果100年内平均会发生5次洪水的情况下,250年内几乎肯定会发生至少一次洪水泛滥;
- 绿色线的概率大概为0.4,表示如果100年内平均发生0.2次,也就是说基本上500年才发生一次,那么250年内发生的概率就会比较小,但也不是不可能。
下面是代码:
1 def compare_poission_exp(): 2 """ 3 This post explained the relation between these two distribution 4 - https://stats.stackexchange.com/a/2094/134555 5 - P(Xt <= x) = 1 - e^(-lambda * x) 6 Now, I suppose lambda=1, just like this example(from wiki, Poisson_distribution): 7 - On a particular river, overflow floods occur once every 100 years on average. 8 :return: 9 """ 10 x = np.arange(20) 11 y1 = 1 - np.power(np.e, -x) # lambda = 1 12 y2 = 1 - np.power(np.e, -0.2*x) # lambda = 0.2 13 y3 = 1 - np.power(np.e, -5*x) # lambda = 1.5 14 print(y1) 15 print(y2) 16 print(y3) 17 fig, ax = plt.subplots(1, 1) 18 ax.plot(x, y1, 'r-', label='lambda=1') 19 ax.plot(x, y2, 'g-', label='lambda=0.2') 20 ax.plot(x, y3, 'b-', label='lambda=5') 21 ax.legend(loc='best', frameon=False) 22 plt.ylabel('Probability') 23 plt.title('CDF of exponential distribution') 24 plt.show() 25 26 compare_poission_exp()
欢迎阅读“概率论与数理统计及Python实现”系列文章
Reference
https://zh.wikipedia.org/wiki/%E9%80%A3%E7%BA%8C%E5%9E%8B%E5%9D%87%E5%8B%BB%E5%88%86%E5%B8%83
https://www.probabilitycourse.com/
https://zh.wikipedia.org/zh-hans/%E6%8C%87%E6%95%B0%E5%88%86%E5%B8%83
http://blog.csdn.net/u010692239/article/details/53112921
https://www.zhihu.com/question/24796044
http://www.ruanyifeng.com/blog/2015/06/poisson-distribution.html
http://www.csee.usf.edu/~kchriste/tools/poisson.pdf
https://en.wikipedia.org/wiki/Poisson_distribution



 浙公网安备 33010602011771号
浙公网安备 33010602011771号