【概率论与数理统计】小结2 - 随机变量概述
注：对随机变量及其取值规律的研究是概率论的核心内容。在上一个小结中，总结了随机变量的概念以及随机变量与事件的联系。这个小结会更加深入的讨论随机变量。
随机变量与事件
随机变量的本质是一种函数（映射关系），在古典概率模型中，“事件和事件的概率”是核心概念；但是在现代概率论中，“随机变量及其取值规律”是核心概念。
随机变量与事件的联系与区别
小结1中对这两个概念的联系进行了非常详细的描述。随机变量实际上只是事件的另一种表达方式，这种表达方式更加形式化和符号化，也更加便于理解以及进行逻辑运算。不同的事件，其实就是随机变量不同取值的组合。在陈希孺的书中，举了一个很好的例子来说明两者之间的差别：
对于随机试验，我们所关心的往往是与所研究的特定问题有关的某个或某些量，而这些量就是随机变量。当然，有时我们所关心的是某个或某些特定的随机事件。例如，在特定一群人中，年收入在万元以上的高收入者，以及年收入在3000元以下的低收入者，各自的比率如何？这看上去像是两个孤立的事件。可是，若我们引入一个随机变量$X$：
$$ X = 随机抽出一个人其年收入 $$
则X是我们关心的随机变量。上述两个事件可分别表示为$ \{X \gt 10000\} $或$ \{X \lt 3000\} $。这就看出：随机事件这个概念实际上包容在随机变量这个更广的概念之内。也可以说，随机事件是从静态的观点来研究随机现象，而随机变量则是一种动态的观点，一如数学分析中的常量与变量的区分那样，变量概念是高等数学有别于初等数学的基础概念。同样，概率论能从计算一些孤立事件的概率发展为一个更高的理论体系，其基本概念就是随机变量。
一下子引用了一大段话，这段话非常清楚的解释了随机变量与事件的区别：就像变量与常量之间的差别那样，这样的差别比起我自己看到的要大得多。做这样的比较也有利于自己更好的理解“随机变量”这个多少有点抽象的概念。
随机变量的分类
随机变量从其可能取的值全体的性质可以分为两大类：离散型随机变量和连续型随机变量。
离散型随机变量
离散型随机变量的取值在整个实数轴上是间隔的，要么只有有限个取值，要么是无限可数的。
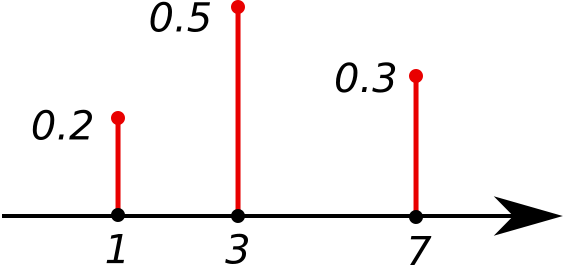
图1：离散型随机变量的概率质量分布函数
常见的离散型随机变量包括以下几种：
- 0-1分布（也叫两点分布或伯努利分布）
- 二项分布
- 几何分布
- 泊松分布
- 超几何分布
连续型随机变量
连续型随机变量的取值要么包括整个实数集$ ( -\infty, +\infty ) $，要么在一个区间内连续，总之这类随机变量的可能取值要比离散型随机变量的取值多得多，它们的个数是无限不可数的。
图2：连续型随机变量的概率密度分布函数
常见的连续型随机变量包括以下几种：
- 均匀分布
- 指数分布
- 正态分布
概率密度函数的性质
随机变量的基本性质
随机变量最主要的性质是其所有可能取到的这些值的取值规律，即取到的概率大小。如果我们把一个随机变量的所有可能的取值的规律都研究透彻了，那么这个随机变量也就研究透彻了。随机变量的性质主要有两类：一类是大而全的性质，这类性质可以详细描述所有可能取值的概率，例如累积分布函数和概率密度函数；另一类是找到该随机变量的一些特征或是代表值，例如随机变量的方差或期望等数字特征。常见的随机变量的性质见下表：
| 缩写 | 全拼 | 中文名 | 解释 |
| CDF | Cumulative Distribution Function | 累计分布函数 | 连续型和离散型随机变量都有，一般用$F(X)$表示 |
| Probability Density Function | 概率密度分布函数 | 连续型随机变量在各点的取值规律，用$f(x)$或$f_X(x)$表示 | |
| PMF | Probability Mass Function | 概率质量分布函数 | 离散随机变量在各特定取值上的概率 |
| RVS | Random Variate Sample | 随机变量的样本 | 从一个给定分布取样 |
| PPF | Percentile Point Function | 百分位数点函数 | CDF的反函数 |
| IQR | Inter Quartile Range | 四分位数间距 | 25%分位数与75%分位数之差 |
| SD | Standard Error | 标准差 | 用于描述随机变量取值的集中程度 |
| SEM | Standard Error of the Mean |
样本均值的估计标准误差， 简称平均值标准误差 |
|
| CI | Confidence Interval | 置信区间 |
表1：常见的随机变量的性质
累计分布函数 vs 百分位数点函数
累积分布函数的定义为$F(x) = P(X \leq x) = \sum P(X \in (-\infty, x])$, 因此累积分布函数是给定$x$求概率；
百分位数点函数是累积分布函数的反函数，是已知概率求符合该条件的$x$.
欢迎阅读“概率论与数理统计及Python实现”系列文章
References
《概率论与数量统计》，陈希孺，中国科学技术大学出版社，2009年2月第一版
中国大学MOOC：浙江大学，概率论与数理统计
https://en.wikipedia.org/wiki/Probability_distribution
