枚举 - 1.熄灯问题

题目描述：

　　有一个由按钮组成的矩阵，其中每行有6个按钮，共5行。每个按钮的位置上有一盏灯。当按下一个按钮后，该按钮以及周围位置(上、下、左、右)的灯都会改变一次。即，如果灯原来是点亮的，就会被熄灭；如果灯原来是熄灭的，则会被点亮。在矩阵角上的按钮改变3盏灯的状态；在矩阵边上的按钮改变4盏灯的状态；其他的按钮改变5盏灯的状态。

 

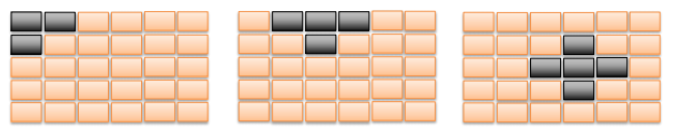
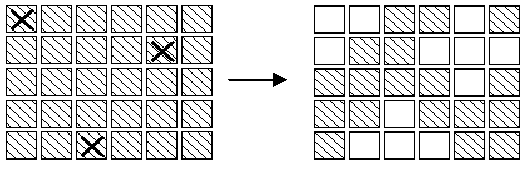
如下图所示，左图表示灯的初始状态为全亮，X表示按下操作，右图表示按下后矩阵的状态。

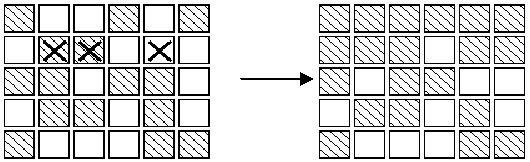
如下图所示，当有相邻两个按钮相继按下时，对它们相邻按钮的状态不发生变化。

对矩阵中的每栈灯设置一个初始状态，请你写一个程序，确定需要按下哪些按钮，恰好使得所有的灯都熄灭。

根据上面的规则，我们知道：

　　1）第2次按下同一个按钮时，将抵消第1次按下时所产生的结果。因此，每个按钮最多只需要按下一次；

　　2）各个按钮被按下的顺序对最终的结果没有影响；

　　3）对第1行中每盏点亮的灯，按下第2行对应的按钮，就可以熄灭第1行的全部灯。如此重复下去，可以熄灭第1、2、3、4行的全部灯。

输入：

第一行是一个正整数N，代表需要解决的案例数。

每个案例5行组成，每一行包括6个数字（0或1）。相邻两个数字之间用单个空格隔开。0表示灯的初始状态是熄灭的，1表示灯的初始状态是点亮的。

输出：

对于每个案例，首先输出一行字符串“PUZZLE #m”，其中m是该案例的序号。

5行组成，每一行包括6个数字（0或1）。相邻两个数字之间用单个空格隔开。其中的1表示需要把对应的按钮按下，0则表示不需要按对应的按钮。

样例输入：
0 1 1 0 1 0
1 0 0 1 1 1
0 0 1 0 0 1
1 0 0 1 0 1
0 1 1 1 0 0

--------------------- 

样例输出：
1 0 1 0 0 1
1 1 0 1 0 1
0 0 1 0 1 1
1 0 0 1 0 0
0 1 0 0 0 0
---------------------

解题思路：

第一想法:

枚举所有可能的按钮(开关)状态, 对每个状态，计算一下最后灯的情况, 看是否都熄灭。
每个按钮有两种状态(按下或不按下)，一共有30个开关, 那么状态数是230, 太多, 会超时 。

如何减少枚举的状态数目呢?
基本思路: 如果存在某个局部, 一旦这个局部的状态被确定, 那么剩余其他部分的状态只能是确定的一种, 或者不多的n种, 那么就只需枚举这个局部的状态即可。 

 

1）因为第1行的各开关操作方案确定的情况下, 这些开关操作过后,将导致第1行某些灯是亮的, 某些灯是灭的。
要熄灭第1行某个亮着的灯(假设位于第i列), 那么唯一的办法就是按下第2行第i列的开关。(因为第1行的开关已经用过了, 而第3行及其后的开关不会影响到第1行)
为了使第1行的灯全部熄灭, 第2行的合理开关操作方案就是唯一的 。

2）第2行的开关操作过后,为了熄灭第2行的灯, 第3行的合理开关操作方案就也是唯一的。以此类推, 最后一行的开关操作方案也是唯一的。
只要第1行的操作方案定下来, 记作A, 那么剩余行的操作方案就是确定唯一的了 。

3）推算出最后一行的开关操作方案, 然后看看最后一行的开关操作过后,最后一行的所有灯是否都熄灭：
如果是, 那么A就是一个解的状态； 如果不是, 那么A不是解的状态, 第1行换个状态重新试试。、

问题简化为：只需枚举第1行的操作方案, 状态数是2^6 = 64 

有没有状态数更少的做法？

枚举第一列, 状态数是2^5 = 32

实现方案：

把按钮矩阵的第一行看作是一个二进制数，通过++来实现。

0 0 0 0 0 0

1 0 0 0 0 0

0 1 0 0 0 0

1 1 0 0 0 0 

0 0 1 0 0 0 

.......

1 1 1 1 1 1

 

具体实现：

使用一个6*8的数组来表示按钮矩阵，因为对于原始的5*6的矩阵上对于边缘上的按钮和中间的按钮所影响的范围是不一样的，而我们想要简化数组下一行值的计算公式，所以多出来的第0行，0列，7列，不属于原press矩阵范围，可全置为0

 

用数组元素 puzzle[i][j] 表示位置 (i, j) 上灯的初始状态：1 表示灯是被点亮的；0 表示灯是熄灭的。

用数组元素 press[i] [j] 表示为了让全部的灯都熄灭，是否要按下位置 (i, j) 上的按钮：1 表示要按下；0 表示不用按下。

因为灯的最后状态（是否按它下一行开关之前）与周围灯是否按按钮有关，如 puzzle[i] [j]，决定它最后状态的相关按钮为 press[i] [j-1] （左），press[i][j]（它本身），press[i] [j+1]（右），press[i-1][j]（上），还有它最初的状态 puzzle[i] [j]。考虑到按两次按钮作用会抵消，需要取它们的和与2的余数，所以只要给定press的第一行的取值，其他行的值可以被相应的计算出来。

puzzle[i] [j] 最后状态公式为:

press[i+1][j] = puzzle[i][j]最后状态 = (press[i][j-1]+press[i][j]+press[i][j+1]+press[i-1][j]+ puzzle[i] [j] ) % 2

注：press[i+1] [j] 由 puzzle[i] [j] 的最后状态决定，灯亮着（值为1）就要关掉它，press值取1，灯是熄灭的（值为0）不用处理，press值取0，它们是相等的，所以press[i+1] [j] = puzzle[i] [j] 最后状态。