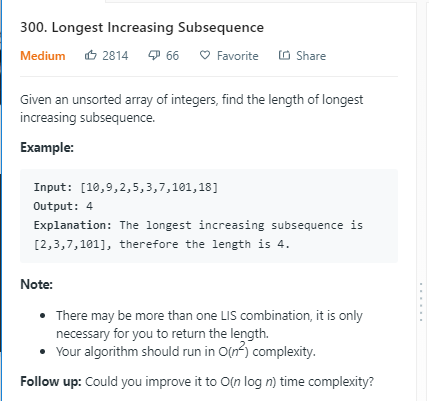
(DP+二分查找) leetcode 300. Longest Increasing Subsequence， 673. Number of Longest Increasing Subsequence
动态规划解法：O(n^2)
class Solution { public: int lengthOfLIS(vector<int>& nums) { if(nums.empty()) return 0; int n = nums.size(); int f[n], res = 0; for(int j=0; j<n; j++){ // case 1 f[j] = 1; //case 2 for(int i=0; i<j; i++){ if(nums[i]<nums[j] && f[i]+1 > f[j]) f[j] = f[i] + 1; } res = max(res, f[j]); } return res; } };
二分查找优化：时间复杂度：O(nlogn)
b[j] : stores length is j (f value is j), smallest ending value.
O(n^2) 的写法是用动态规划，f[i]里存储数组索引为i时的最长上升子序列的长度。而在用二分查找时，设置b[k]来存储当f[i]的值是j时（即最长上升子序列的长度为j时），这个序列的最后一个值（最小的）。遍历n次，每次都二分查找到b[k]里最大那个小于nums[i]的数字, 然后将b[j+1] 替换为 nums[i].
class Solution { public: int lengthOfLIS(vector<int>& nums) { int n = nums.size(); if(n==0) return 0; int b[n+1]; //b[i]: when f value is i, smallest nums value(ending value) int top=0; //top一定要初始化 否则会指针溢出 b[0] = INT_MIN; //O(n) for(int i=0; i<n; i++){ // b[0]...b[top] find the last value b[j] which is smaller than nums[i] int start = 0, stop = top; int mid, j; //O(logn) while(start<= stop){ mid = (start + stop)/2; if(b[mid]<nums[i]){ j = mid; //找到一个 先存下来 start = mid+1; //然后在后面找，因为要找最后一个比nums[i]小的 } else stop = mid-1; } b[j+1] = nums[i]; //f[i] = j+1 if(j+1 > top) top = j+1; //更新top } //b[0]...b[top] //b[top] stores the smallest ending value for an increasing sequence with length top return top; //top的长度就是f[i]的值，即LIS } };
这道题的贪心+二分法的时间复杂度是O(nlogn), 几个月后又重做了一遍题目，发现自己之前写的题解一点也不通俗易懂== 反正我是没读懂。。。
总结来说：维护一个递增的数组tail[i]，表示长度为i+1的子序列的最小末尾元素为tail[i]，最后返回这个数组的长度即end+1就是答案。
遍历nums，若tail[end] < nums[i] 则直接插入到tail的末尾；否则，每次在tail中找到第一个大于等于nums[i]的元素，用nums[i]替换。
class Solution { public: int lengthOfLIS(vector<int>& nums) { //二分搜索：tail[i]:存储长度为i+1的子序列的最小末尾元素 int n = nums.size(); if(n<2) return n; vector<int> tail; tail.push_back(nums[0]); int end = 0; //tail最末的索引 for(int i=1; i<n; i++){ if(nums[i] > tail[end]){ tail.push_back(nums[i]); end++; } else{ // nums[i] < tail[end] // 二分法在tail里找到第一个大于nums[i]的元素，用nums[i]替换 int left = 0, right = end; while(left + 1 < right){ int mid = (left + right)>>1; if(tail[mid]<=nums[i]){ left = mid; } else right = mid; } if(tail[left] >= nums[i]) tail[left] = nums[i]; else tail[right] = nums[i]; } //cout<<end+1<<endl; // for(auto c : tail) cout<<"tail"<<" "<<c<<endl; } return end+1; } };
延续上题动态规划的思想，并设置一个数组t[i]来记录 数组中索引为i时最长上升子序列f[i]对应出现的个数。
注意一下特殊情况[2,2,2,2,2] 时输出为5不是1。[1,2,6,5,4]时输出为3。
class Solution { public: int findNumberOfLIS(vector<int>& nums) { int n = nums.size(); if(n==0) return 0; int f[n]; int t[n]; //记录长度为f[i]的子序列出现的个数 for(int i=0; i<n; i++){ //初始化 f[i] = 1; t[i] = 1; for(int j=0; j<i; j++){ if(nums[i] > nums[j]){ if(f[j]+1 > f[i]){ f[i] = f[j]+1; t[i] = t[j]; } else if(f[j]+1 == f[i]) t[i] += t[j]; } } } int result = 0, len = 0; for(int i=0; i<n; i++){ if(f[i] > result){ result = f[i]; len = t[i]; } else if(f[i] == result) len += t[i]; //[2,2,2,2,2] output:5 //cout<<f[i]<<" "<<len<<endl; } return len; } };
