背包问题

1. 01背包问题：

 

 

 

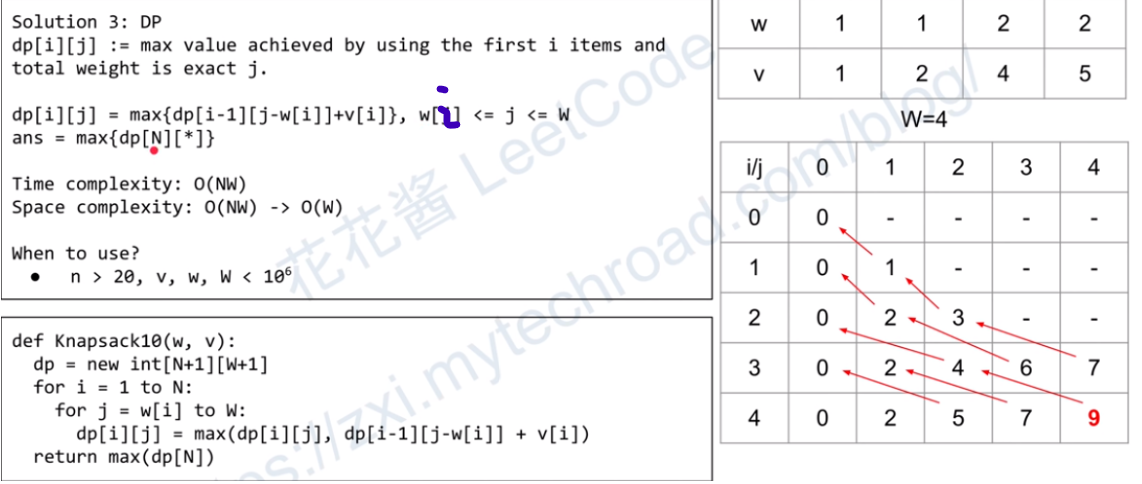
1）用二维动态规划表示：f[i][j] 为只看前 i 个物品，这些物品的总体积是 j 的情况下，总价值最大是多少。

result = max(f[n][0~V])     # V 为背包容量

f[i][j]  = max( f[ i - 1 ][j], f[ i - 1 ][ j - v[i] ] )

a) 不选第 i 个物品： f[i][j] = f[ i - 1 ][j]

b) 选第i个物品：f[i][j] = f[ i - 1 ][ j - v[i] ]

初始化：f[0][0] = 0

 

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010;
int n, m;     //n为物品个数，m为背包容量
int f[N][N];    //堆里初始化为0 f[i][j] : 只看前i个物品，背包剩余体积为j时，总价值为多少
int v[N], w[N];      //物品容量和背包价值

int main(){
    cin>>n>>m;
    for(int i=1; i<=n; i++)
        cin>>v[i]>>w[i];
        
    for(int i=1; i<=n; i++){
        for(int j=1; j<=m; j++){
            f[i][j] = f[i-1][j];   //不选第i件物品
            if(j >= v[i])
                f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i]);
        }
    }
    int res = 0;
    for(int i=1; i<=m; i++)
        res = max(res, f[n][i]);
    cout<<res<<endl;
    return 0;
}

化简为一维数组：

最后输出的f[m]表示：总体积小于等于m的最大价值

因为是把所有的f[i]都初始化为0了。

若体积为k时达到了最大价值，若k<m

则 f[k] = max_w

 

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010;
int n, m;     //n为物品个数，m为背包容量
int f[N];    
int v[N], w[N];      //物品容量和背包价值

int main(){
    cin>>n>>m;
    for(int i=1; i<=n; i++)
        cin>>v[i]>>w[i];
        
    for(int i=1; i<=n; i++)
        for(int j=m; j>=v[i]; j--)
            f[j] = max(f[j], f[j-v[i]] + w[i]);
     
        
    cout<<f[m]<<endl;    //体积小于等于m的情况下，最大价值是多少
    return 0;
}