(分治法、归并排序) Count Inversions in an array

题意：对于一个序列，若存在 i<j , a[j]>a[j] 则是一组逆序对；若这个序列是升序的，则逆序对个数为0；若是降序的，逆序对个数最大。

分而治之模板：

Divide and Conquer Paradigm:

1) divide into smaller suibproblems;

2) conquer via recursive calls;

3) combine solutions of subproblems into one for the original problem.

举例：

归并排序算法：

 

 

归并排序是稳定算法。

 

 

如何用merge sort来求逆序对的思路：

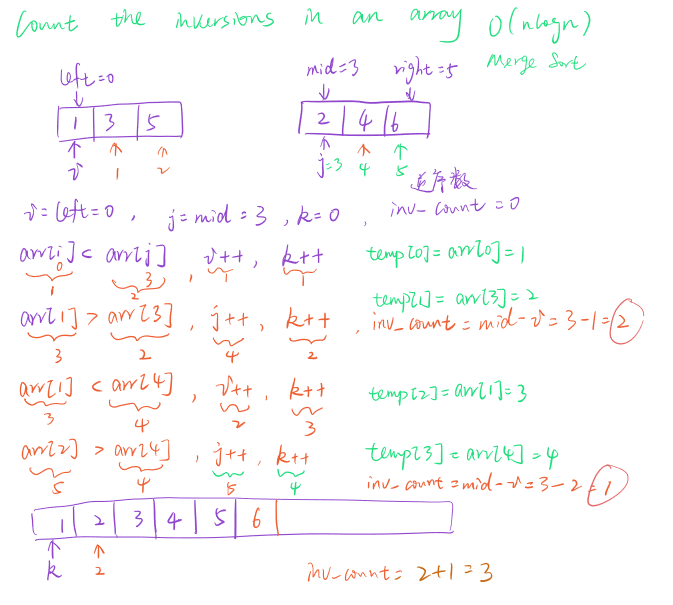
递归写法：

            

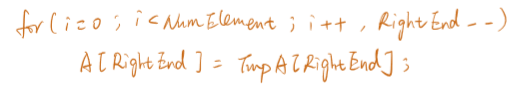
// C++ program to Count 
// Inversions in an array 
// using Merge Sort 
#include <bits/stdc++.h> 
using namespace std; 

int _mergeSort(int arr[], int temp[], int left, int right); 
int merge(int arr[], int temp[], int left, int mid, int right); 

/* This function sorts the input array and returns the 
number of inversions in the array */
int mergeSort(int arr[], int array_size) 
{ //归并排序接口
    int temp[array_size]; 
    return _mergeSort(arr, temp, 0, array_size - 1); 
} 

/* An auxiliary recursive function that sorts the input array and 
returns the number of inversions in the array. */
int _mergeSort(int arr[], int temp[], int left, int right) 
{   //分-递归
    int mid, inv_count = 0; 
    if (right > left) 
    { 
        /* Divide the array into two parts and 
        call _mergeSortAndCountInv() 
        for each of the parts */
        mid = (right + left) / 2; 

        /* Inversion count will be sum of 
        inversions in left-part, right-part 
        and number of inversions in merging */
        inv_count = _mergeSort(arr, temp, left, mid); 
        inv_count += _mergeSort(arr, temp, mid + 1, right); 

        /*Merge the two parts*/
        inv_count += merge(arr, temp, left, mid + 1, right); 
    } 
    return inv_count; 
} 

/* This funt merges two sorted arrays 
and returns inversion count in the arrays.*/
int merge(int arr[], int temp[], int left, 
                        int mid, int right) 
{  //合并
    int i, j, k; 
    int inv_count = 0; 

    i = left; /* i is index for left subarray*/
    j = mid; /* j is index for right subarray*/
    k = left; /* k is index for resultant merged subarray*/
    while ((i <= mid - 1) && (j <= right)) 
    { 
        if (arr[i] <= arr[j]) 
        { 
            temp[k++] = arr[i++]; 
        } 
        else
        { 
            temp[k++] = arr[j++]; 

            /* this is tricky -- see above 
            explanation/diagram for merge()*/
            inv_count = inv_count + (mid - i); 
        } 
    } 

    /* Copy the remaining elements of left subarray 
(if there are any) to temp*/
    while (i <= mid - 1) 
        temp[k++] = arr[i++]; 

    /* Copy the remaining elements of right subarray 
(if there are any) to temp*/
    while (j <= right) 
        temp[k++] = arr[j++]; 

    /*Copy back the merged elements to original array*/
    for (i = left; i <= right; i++) 
        arr[i] = temp[i]; 

    return inv_count; 
} 

// Driver code 
int main() 
{ 
    int arr[] = { 1, 20, 6, 4, 5 }; 
    int n = sizeof(arr)/sizeof(arr[0]); 
    int ans = mergeSort(arr, n); 
    cout << " Number of inversions are " << ans; 
    return 0; 
} 

 参考链接：https://www.geeksforgeeks.org/counting-inversions/