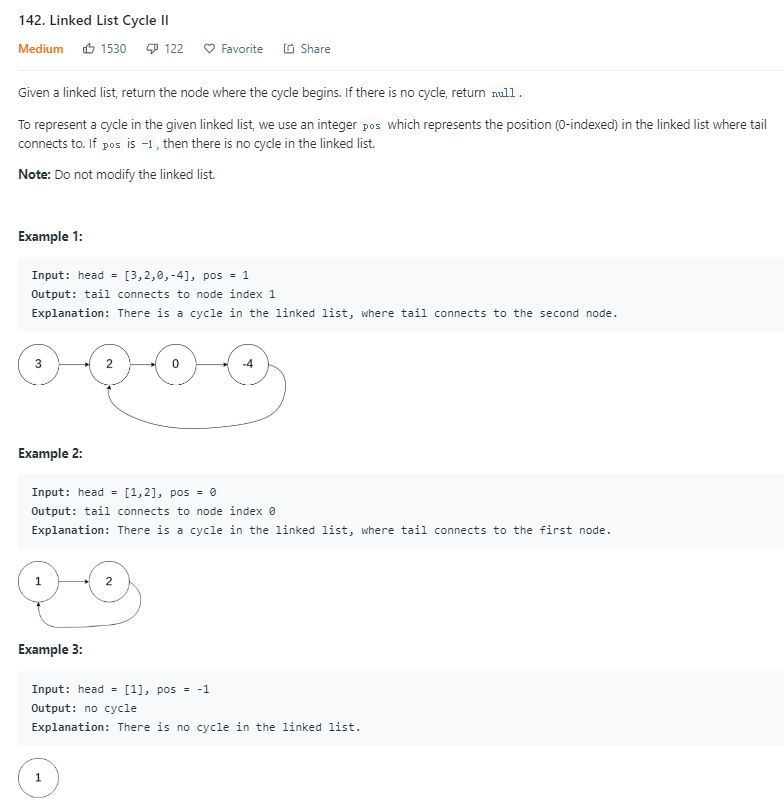
(快慢指针)（链表中的环）leetcode 141. Linked List Cycle, 142. II, 287(二分法)

思路：

解法一：快慢指针，一开始都指向头结点，快指针fast每次走两步，慢指针slow每次走1步。若链表存在环，则fast肯定会追上slow，否则链表遍历完后，返回false。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        //快慢指针
        ListNode* slow = head, *fast = head;
        while(fast && fast->next){
            slow = slow->next;
            fast = fast->next->next;
            if(slow == fast)
                return true;
        }
        return false;
    }
};

解法二：hashset

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        //hash
        unordered_set<ListNode*> visited;  //存储访问过的结点
        while(head){
            if(visited.count(head))
                return true;
            visited.insert(head);
            head = head->next;
        }
        return false;
    }
};

 

 快慢指针相遇时，让快指针位置不变，慢指针从head开始，两个指针同时开始走，都走一步，相遇的位置就是环的起点。

参考链接：https://www.bilibili.com/video/av48348861?from=search&seid=5980719733722263225

假设快慢指针meet到的时候，慢指针走的距离是a+b, 而快指针的速度是慢指针的两倍，所以快指针走的距离是2(a+b) = a+b + n(b+c)

通过最后的公式：a = (n-1)(b+c) + c 可知 slow从head开始走，fast从meet点开始走，每次只走一步（即与slow速度相同），则最终fast走整数个(b+c)后，加上c，可与a在cycle点相遇。

/**
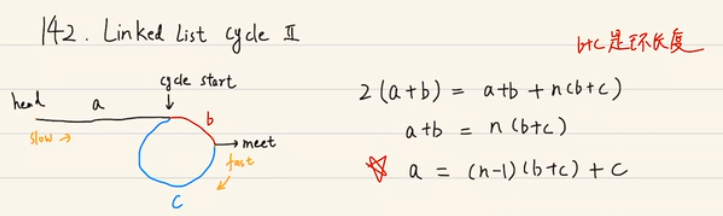
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* slow = head, *fast = head;
        while(fast && fast->next){
            slow = slow->next;
            fast = fast->next->next;
            if(slow == fast){
                slow = head;
                while(slow!=fast){
                    slow = slow->next;
                    fast = fast->next;
                }
                return slow;
            }
        }
        return NULL;
    }
};

 

 

 

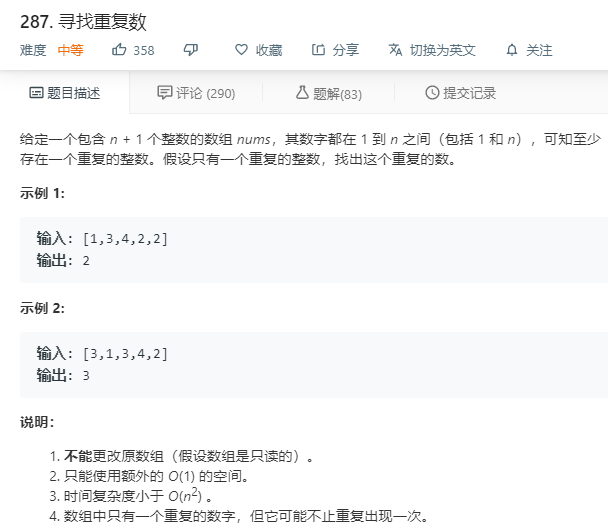
思路1：二分法

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        // 二分法：对要定位的“数”做二分，而不是对数组的索引做二分。
        // 要定位的“数”根据题意在 1 和 n 之间，每一次二分都可以将搜索区间缩小一半
        int l = 1, r = nums.size()-1;
        while(l < r){
            int mid = (l+r)/2;
            int cnt = 0;
            for(int num : nums){
                if(num <= mid) cnt++; 
            }
            if(cnt <= mid) l = mid+1;
            else r = mid;
        }
        return l;
    }
};

 

思路2：快慢指针 https://www.bilibili.com/video/av62810942/

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        // 转化为找一个链表的环的起点位置 => 快慢指针
        // 快指针每次移动2，慢指针移动1，当它们相遇时：
        // 把慢指针移回开头，再同时以1前进，最后两个指针相遇的位置即为环的起点位置
        int fast = 0, slow = 0;   //快慢指针指向数组的索引
        do{
            fast = nums[nums[fast]];
            slow = nums[slow];
        }while(fast!=slow);
        slow = 0;
        while(fast != slow){
            fast = nums[fast];
            slow = nums[slow];
        }
        return slow;
    }
};