（动态规划）leetcode 857: Minimum Cost to Hire K Workers, 42: Trapping Rain Water

 

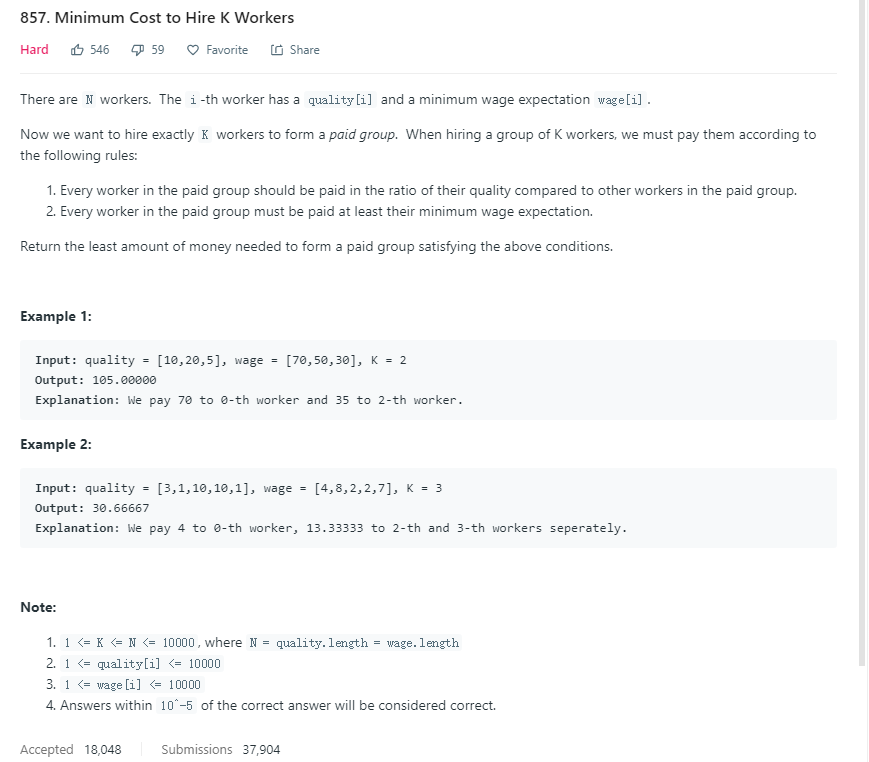
有N个工人，第i个工人的质量是quality[i]，最小工资期盼是wage[i]，现在想雇K个工人组成一个支付组，返回所需的最小花费。有两个条件：

1. K个工人的质量和给他开的工资的比例是相同的。
2. 每个工人都要满足他的最小期望工资。

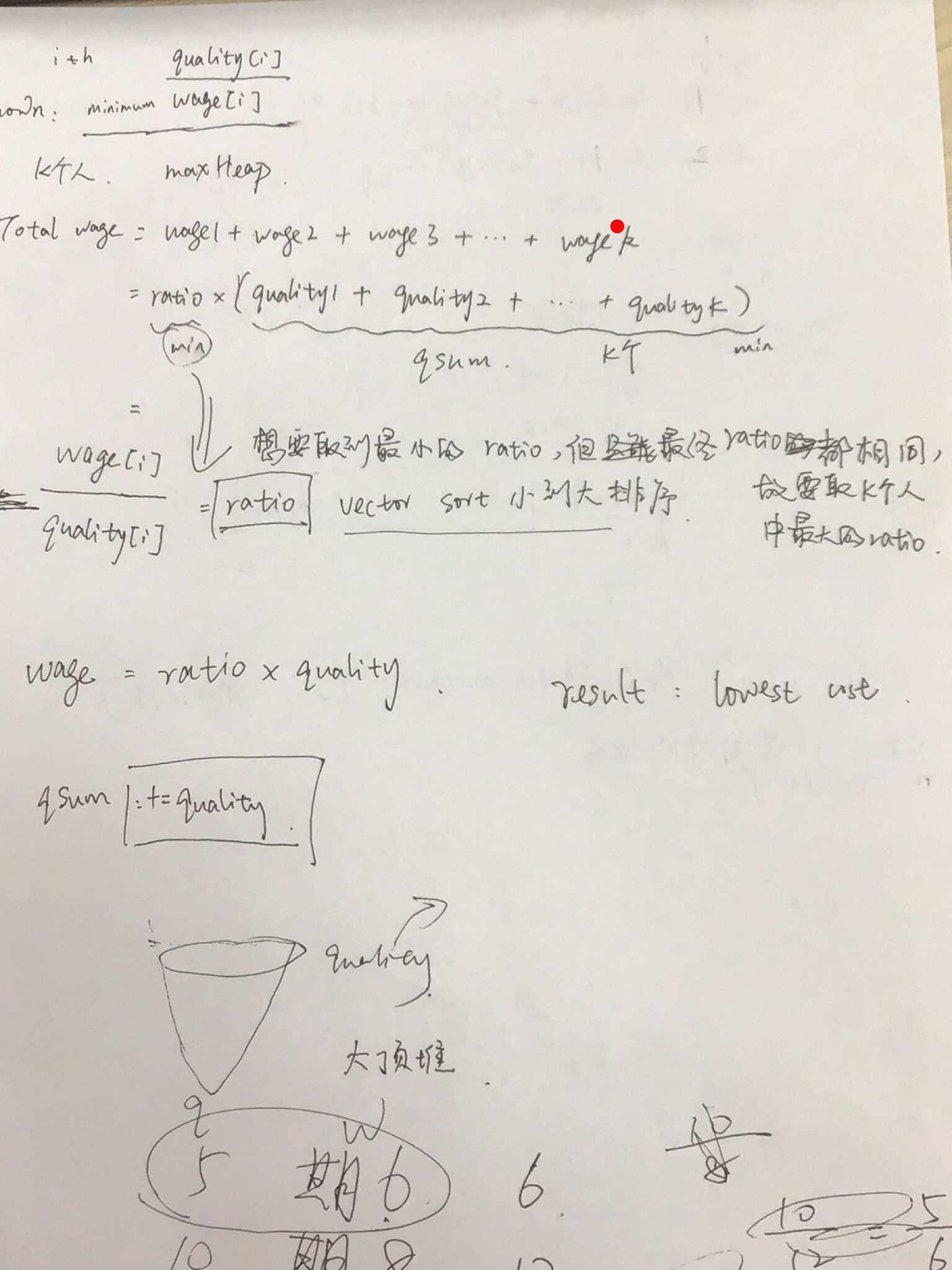
解法：最大堆: priority_queue。首先对付工资和质量的比率进行排序wage/quality，同时记录quality，也就是(wage/quality, quality)，代表一个工人情况，比率越大说明工人效率越低。选定的K个人最后要按照相同的比率来支付工资，为了保证每个人的最低工资标准，只能选定比率最高的人的比率来支付工资。每个人的支付工资：wage = ratio * quality，总的支付工资：total wage = ratio * (total quality)，在ratio相同的情况下，总的quality越小越好。用一个变量res记录最小花费，初始为最大浮点数。使用sort()从小到大排列工资比率ratio，用一个变量qsum累加quality，用一个最大堆记录当前的quality，堆顶是最大的quality，如果堆长度等于K+1，就弹出quality最大的，同时qsum中去掉这个最大值。堆满足K个工人的时候，每次都计算qsum * ratio，和res 比较取小的。

class Solution {
public:
    double mincostToHireWorkers(vector<int>& quality, vector<int>& wage, int K) {
        vector<pair<double, int>> ratio;
        for(int i=0; i<wage.size(); ++i){
            ratio.emplace_back(double(wage[i])/quality[i], quality[i]);
        }
        sort(ratio.begin(), ratio.end());
        double res = DBL_MAX, qsum = 0;
        priority_queue<int> pq;  //大顶堆
        for(auto ratio_ : ratio){
            qsum += ratio_.second;
            pq.push(ratio_.second);
            if(pq.size() > K){
                qsum -= pq.top();
                pq.pop();
            }
            if(pq.size() == K){
                res = min(res, qsum * ratio_.first);
            }
        }
        return res;
    }
};

 

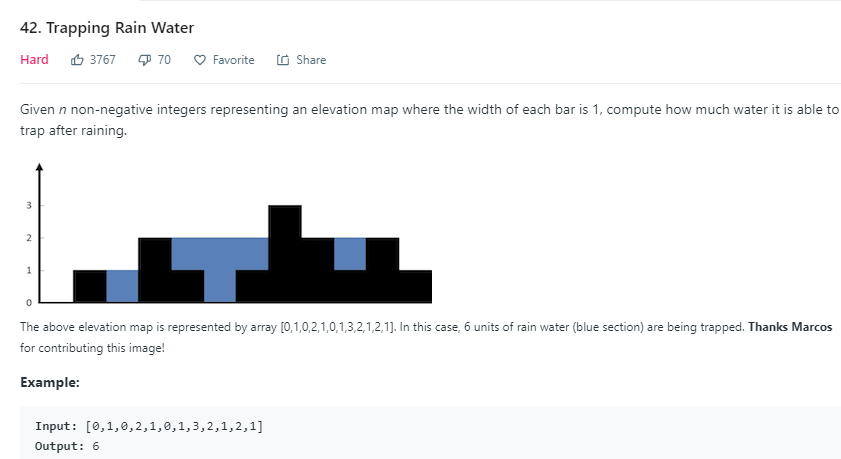
动态规划：索引为0和s-1处不考虑，因为无法积水。所以求积水的面积从索引1到s-2。

class Solution {
public:
    int trap(vector<int>& height) {
        int s = height.size();
        if(s==0)
            return 0;
        int ans = 0;
        vector<int>leftmax(s), rightmax(s);
        leftmax[0] = height[0];
        rightmax[s-1] = height[s-1];
        for(int i=1; i<s; i++){
            leftmax[i] = max(leftmax[i-1], height[i]);
        }
        
        for(int j=s-2; j>=0; j--)
            rightmax[j] = max(rightmax[j+1], height[j]);
        
        for(int i=1; i<s-1; i++)
            ans += min(leftmax[i], rightmax[i])-height[i];
        
        return ans;
    }
};

 

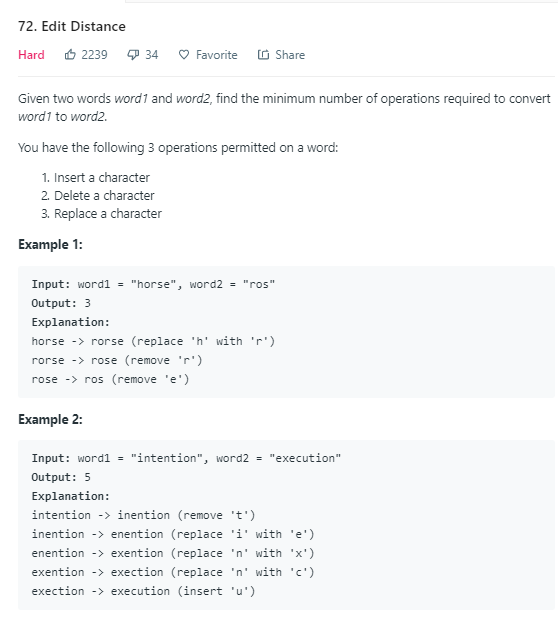
思路：动态规划策略就是让word1的最后一个字符等于word2的最后一个字符，有三种操作。则只需要考虑子问题了。

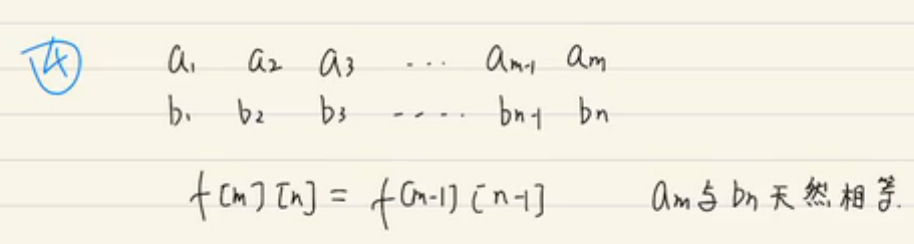
class Solution {
public:
    int minDistance(string word1, string word2) {
        //dp[i][j]记录从word1的第i-1个字符，word2的第j-1个字符需要的操作数
        int n = word1.size(), m = word2.size();
        vector<vector<int>> dp(n+1, vector<int>(m+1,0));
        for(int i=0; i<n+1; ++i){
            for(int j=0; j<m+1; ++j){
                //边界条件
                if(i==0) {
                    //word1为空，word1需要insert j次变为word2
                    dp[i][j] = j;
                    continue;
                }
                if(j==0){
                    dp[i][j] = i;  //word2为空，word1需要delete i次才为空
                    continue;
                }
                   
                if(word1[i-1] == word2[j-1]) //贪心
                    dp[i][j] = dp[i-1][j-1];
                else
                    dp[i][j] = min(dp[i][j-1], min(dp[i-1][j], dp[i-1][j-1]) ) + 1;   
            }
        }
        return dp[n][m];
    }
};