动态规划：leetcode 1039: Minimum Score Triangulation of Polygon，376：Wiggle Subsequence，678：Valid Parenthesis String

 

 

 

思路：动态规划dp[i][j]：从第i个点到第j个点的最小值。dp[i][j] = min(dp[i][j], dp[i][k]+dp[k][j]+A[i]*A[j]*A[k])

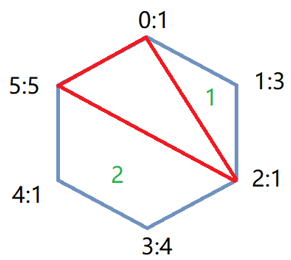
如下图：此时求dp[0][5]，以（0,5）为边，在（0,5）之间遍历三角形的顶点，构成的每个三角形将原图形分为三部分：三角形，子图形1，子图形2。（默认第一个顶点序号0和最后一个顶点5是相连的）。

注意一下：边界范围，len从3到s（s为顶点数），也就是说, 当i为0时：j范围从i+2到s-1，即默认顶点0和顶点n-1是连接的。而k是在i，j的范围内一次遍历。

 

class Solution {
public:
    int minScoreTriangulation(vector<int>& A) {
        int dp[50][50];
        memset(dp, 0, sizeof(dp));
        int s = A.size();
        for(int len=3; len<=s; len++){
            for(int i=0; i+len-1<s; i++){
                int j = i+len-1;
                dp[i][j] = INT_MAX;
                for(int k=i+1; k<j; k++)
                    dp[i][j] = min(dp[i][j], dp[i][k]+dp[k][j]+A[i]*A[j]*A[k]);
            }
        }
        return dp[0][s-1];
    }
};

 

题意：寻找最长的波动数组，即输入数组中，后一个数减前一个数的差为：一正一负，或一负一正。

思路：换句话说，输入数组里的数字需要是：大小大小..... 或 小大小大..... 排列。可以设置两个数组：up[i] 和 down[i], 这里有三种情况：

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int s = nums.size();
        if(s == 0) return 0;
        int up[s], down[s];
        up[0] = down[0] = 1;
        for(int i=1; i<s; i++){
            if(nums[i]>nums[i-1]){
                down[i] = down[i-1];
                up[i] = down[i-1]+1;
            }
            else if(nums[i]<nums[i-1]){
                down[i] = up[i-1]+1;
                up[i] = up[i-1];
            }
            else{
                up[i] = up[i-1];
                down[i] = down[i-1];
            }
        }
        return max(up[s-1], down[s-1]);
    }
};

 

解法一：动态规划

1) 迭代法，自下而上，注意数组要初始化呀！

class Solution {
public:
    bool checkValidString(string s) {
        int l = s.length();
        if(l==0) return true;
        int dp[l][l];
        memset(dp, 0, sizeof(dp));
        for(int i=0; i<l;++i){
            if(s[i]=='*')
                dp[i][i] = 1;
        }
        for(int len=2; len<=l; ++len){
            for(int i=0; i<=l-len; ++i){
                int j = i+len-1;
                if((s[i]=='(' || s[i]=='*') && (s[j]==')' || s[j]=='*')){
                    if(len==2 || dp[i+1][j-1]){
                        dp[i][j] = 1;
                        continue;
                    }

                }
                
                for(int k=i;k<j;++k){
                    if(dp[i][k] && dp[k+1][j]){
                        dp[i][j] = 1;
                        break;
                    }
                }
                
            }
        }
        return dp[0][l-1];
    }
};

2）递归法：（超时了==）

class Solution {
public:

    bool checkValidString(string s) {
        int l = s.length();
        vector<vector<int>> m(l, vector<int>(l,0));
        return isValid(s,0,l-1,m);
    }
    bool isValid(string& s, int i, int j, vector<vector<int>>& m){
        if(i>j) return true;
        if(m[i][j]>0) return m[i][j];
        if(i==j) return m[i][j] = (s[i]=='*');
        if((s[i]=='('||s[i]=='*') && (s[j]==')'|| s[j]=='*')&&isValid(s,i+1,j-1,m))
            return m[i][j]=1;
        for(int k=i; k<j; ++k){
            if(isValid(s,i,k,m) && isValid(s,k+1,j,m))
                return m[i][j]=1;
        }
        return m[i][j]=0;
    }
};

解法三：这个方法是真的快！

class Solution {
public:
    bool checkValidString(string s) {
        int min_op = 0; //强制匹配左括号
        int max_op = 0; //可选匹配左括号
        for(char c:s){
            if(c=='(') 
                ++min_op;
            else
                --min_op;
            if(c!=')')
                ++max_op;
            else
                --max_op;
            if(max_op<0)
                return false;  //右括号比左括号和*加起来的数量还要多
            if(min_op<0)
                min_op = 0;
        }
        return min_op==0 ;
    }
};