(动态规划、栈)leetcode 84. Largest Rectangle in Histogram, 85. Maximal Rectangle

 

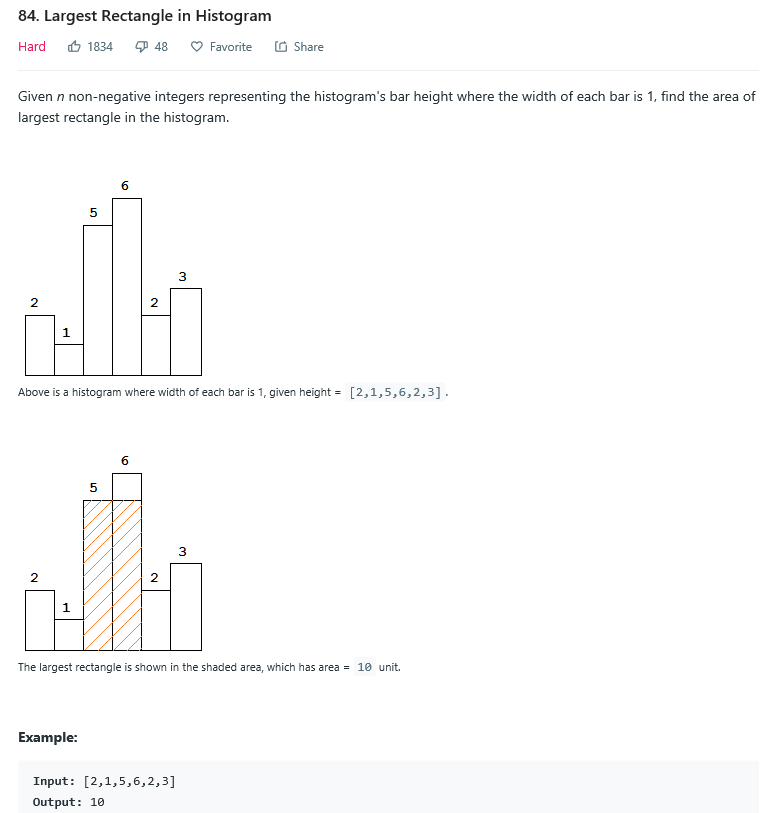
题意：求直方图中矩形的最大面积。

思路：维护一个栈，用来保存递增序列（存储索引），即寻找直方图的局部峰值。因为若想要直方图矩形面积最大，需要尽可能的使得连续的矩形多，且最低一块的高度要高。

时间复杂度：O(n)

 

对于一个索引的高度，如果我们知道左侧比它高度小的位置和右侧高度比它小的位置，就知道以该点为高度的矩形面积。

1）若遇到当前heights[i] 小于栈顶元素heights[s.top()]，就将栈顶元素弹出，栈顶元素为将要计算的该位置的高度。

2）若弹出之后，栈为空，则矩形的宽为i，因为当栈为空，s.top() 也没有值；否则为(i-s.top()-1), 再计算矩形面积。

trick：在heights数组后加上一个0，使原先的最后一个板子也可以被处理。

 

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        stack<int> s;
        int height=0, area=0, max_area=0;
        if(heights.empty()) return 0;
        heights.push_back(0);
        int size = heights.size();
        
        for(int i=0; i<size;i++){
            
                if(s.empty() || heights[i] >= heights[s.top()] ){
                    s.push(i);
                }
                else{
                    height = heights[s.top()];
                    s.pop();
                    area = height * (s.empty() ? i : (i-s.top()-1));
                    max_area = max(max_area, area);
                    i--;   //i位置的最大矩形还未计算
                }
        }
        return max_area;
    }
};

 

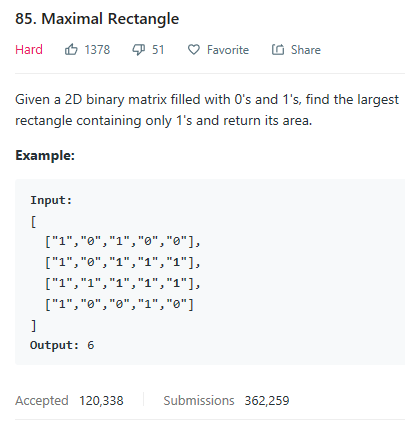
题意：寻找0，1数字中，最大面积的矩形。

思路：可以遍历数组的每一行，维护一个和这个数组第二维同等大小的vector容器用来存储该行的直方图的高度。继而转化为84题直方图的思路。

注意：matrix是char类型的！！！记得比较时 是与字符1， 即 matrix[i][j] == '1'

要在高度数组h的后面加上0，方便计算最后一个元素。

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        if(matrix.empty() || matrix[0].empty()) return 0;
        int s = matrix[0].size();
        int area = 0;
        vector<int> h(s, 0);
        for(int i=0; i<matrix.size();i++){
            for(int j=0; j<s; j++){
                if(matrix[i][j] == '1')
                    h[j] +=1;
                else
                    h[j] = 0;
            }
            area = max(area, maxRectangle(h)); 
        }
        return area;
    }
    
    int maxRectangle(vector<int>& hec){
        int height=0, area=0, max_area=0;
        hec.push_back(0);
        int size = hec.size();
        stack<int> st;
        for(int i=0; i<size;i++){
            if(st.empty() || hec[st.top()]<=hec[i])
                st.push(i);
            else{
                height = hec[st.top()];
                st.pop();
                area = height*(st.empty() ? i: (i-st.top()-1));
                max_area = max(area, max_area);
                i--;
            }
            
        }
        return max_area;
    }
};