图-基础

1. 图的表示：

1）邻接矩阵：

a. 表示无向图：

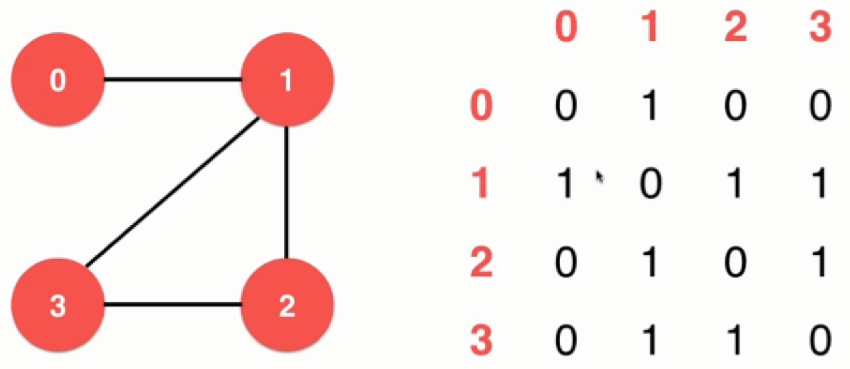
b. 表示无向图：

 

#include<stdio.h>
#include<stdlib.h>
#include<vector>
#include<iostream>
#include<assert.h>
using namespace std;

//稠密图 - 邻接矩阵
class DenseGraph {
private:
    int n, m;  //顶点，边
    bool directed;   //有向或无向
    vector<vector<bool>> g;   //邻接矩阵

public:
    DenseGraph(int n, bool directed) {
        this->n = n;
        this->m = 0;
        this->directed = directed;
        for (int i = 0; i < n; i++) {
            g.push_back(vector<bool>(n, false));
        }
    }
    ~DenseGraph()
    {

    }
    int V() { return n; }  //返回顶点数
    int E() { return m; }  //返回边数

    void addEdge(int v, int w) {
        assert(v >= 0 && v < n);
        assert(w >= 0 && w < n);

        if (hasEdge(v, w))
            return;   //若已经有边，直接return

        g[v][w] = true;  //有向图

        if (v!=w &&!directed) {
            //无向图
            g[w][v] = true;
        }
        m++;
    }
    bool hasEdge(int v, int w) {
        //判断v和w之间是否已经存在边 （不包括平行边）
        assert(v >= 0 && v < n);
        assert(w >= 0 && w < n);
        return g[v][w];  //返回为true或false
    }
};

 

 2）邻接表：

a. 无向图：

第一行：0 和 1 相连；

第二行：1 和 0，2，3 相连；

第三行：2 和 1，3 相连；

第四行：3 和 1，2 相连。

b. 有向图：

 

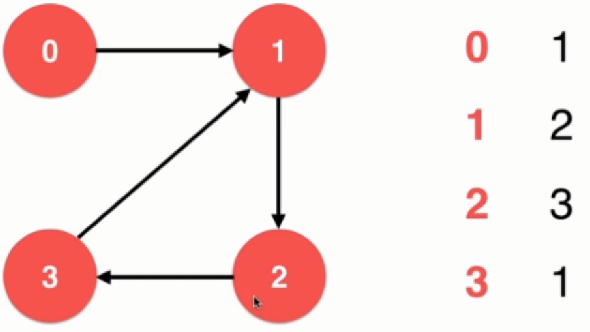
 邻接表适合表示一个稀疏的图， 邻接矩阵适合表示一个稠密的图。

 若有平行边，邻接表会最多需要O(n)的时间复杂度， 去把平行边消除。

#include<stdio.h>
#include<stdlib.h>
#include<vector>
#include<iostream>
#include<assert.h>
using namespace std;

//稀疏图 - 邻接表
class SparseGraph {
private:
    int n, m;  //顶点，边
    bool directed;   //有向或无向
    vector<vector<int>> g;   // 邻接表 每一行存储的是顶点编号

public:
    SparseGraph(int n, bool directed) {
        //构造函数来初始化
        this->n = n;
        this->m = 0;
        this->directed = directed;
        for (int i = 0; i < n; i++) {
            g.push_back(vector<int>() );
        }
    }
    ~SparseGraph()
    {

    }
    int V() { return n; }
    int E() { return m; }

    void addEdge(int v, int w) {
        assert(v >= 0 && v < n);
        assert(w >= 0 && w < n);

        if (hasEdge(v, w))
            return;   //若已经有边，直接return

        g[v].push_back(w);  //v和w相连

        if (v!=w && !directed) {
            //无向图（不自环）
            g[w].push_back(v);
        }
        m++;
    }
    bool hasEdge(int v, int w) {
        //判断v和w之间是否存在边
        assert(v >= 0 && v < n);  //判断v和w不越界
        assert(w >= 0 && w < n);

        for (int i = 0; i < g[v].size();i++) { //O(n)复杂度 寻找平行边
            if (g[v][i] == w)
                return true;
            return false;
        }
        return g[v][w];  //返回为true或false
    }
};

 

2. 遍历邻边

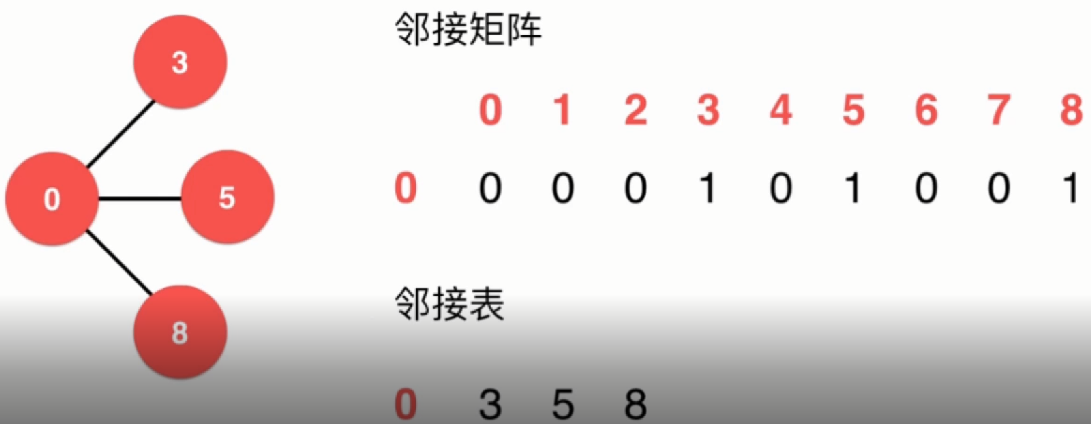
邻接矩阵遍历临边需要O(v)的时间复杂度，v为顶点个数。

所以最好使用邻接表。

 

用BFS和DFS来遍历图:

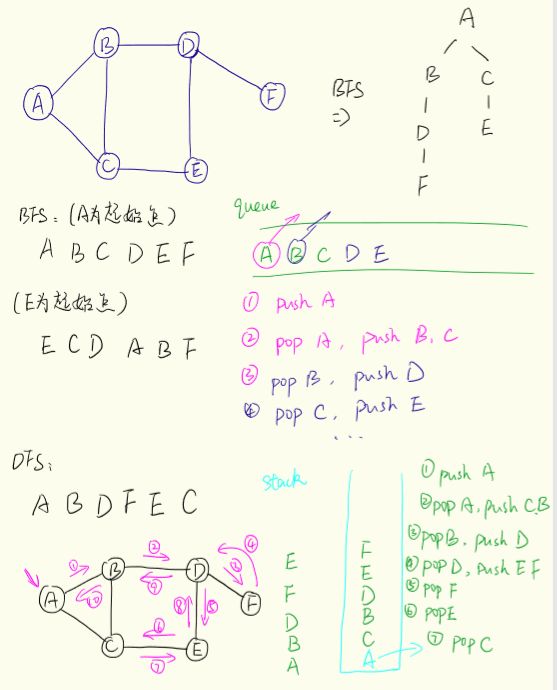
#字典
graph ={
    "A":["B","C"],
    "B":["A","C","D"],
    "C":["A","B","D","E"],
    "D":["B","C","E","F"],
    "E":["C", "D"],
    "F":["D"]
}

 

def BFS(graph, s):    #s起点
    queue = []
    queue.append(s)
    seen = set()
    seen.add(s)
    
    while(len(queue)>0):
        vertex = queue.pop(0)   #取出队首元素
        nodes = graph[vertex]
        for w in nodes:
            if w not in seen:
                queue.append(w)
                seen.add(w)
        print (vertex)

输出：

BFS(graph, "A")

 

DFS：

def DFS(graph, s):    #s起点
    stack = []
    stack.append(s)
    seen = set()
    seen.add(s)
    
    while(len(stack)>0):
        vertex = stack.pop()   #取出队首元素
        nodes = graph[vertex]
        for w in nodes:
            if w not in seen:
                stack.append(w)
                seen.add(w)
        print (vertex)

DFS(graph, "A")

输出所有结点的父亲：

def BFS(graph, s):    #s起点
    queue = []     #数组
    queue.append(s)
    seen = set()    #集合
    seen.add(s)
    parent = {s: None}     #字典 来记录某个结点的父亲，起始点的父亲为空
    
    while(len(queue)>0):
        vertex = queue.pop(0)   #取出队首元素
        nodes = graph[vertex]
        for w in nodes:
            if w not in seen:
                queue.append(w)
                seen.add(w)
                parent[w] = vertex
        #print (vertex)
    return parent

 

parent = BFS(graph, "A")
for key in parent:
    print(key, parent[key])