队列 102 Binary Tree Level Order Traversal

队列的基本应用 - 广度优先遍历

1）树 ： 层序遍历；

2）图：无权图的最短路径。

使用队列来实现二叉树的层序遍历，需要多关注一个层数的信息

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int> > res;   //存储最终输出的二维列表
        if(root == NULL)
            return res;
        queue< pair<TreeNode*, int> > q;    //将当前结点与它在第几层成对
        q.push(make_pair(root, 0));
        while(!q.empty()){
            TreeNode* node = q.front().first;
            int level = q.front().second;
            q.pop();
            
            if(level == res.size())  //若相等则说明res中还不存在这一层，因为level从0开始计数，res从1开始
                //这个结点在一个新的层中,在res中新加一层
                res.push_back(vector<int>());
            
            res[level].push_back(node->val);
            
            if(node->left)
                q.push(make_pair(node->left, level+1));
            if(node->right)
                q.push(make_pair(node->right, level+1));
        }
        return res;
    }
};

解法二：<推荐> 比解法一通用，更方便。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        if(!root) 
            return {};
        vector<vector<int>> res;
        queue<TreeNode* > q{{root}};
        while(!q.empty()){
            vector<int> oneLevel;
            for(int i = q.size(); i>0; i--){
                //因为q的大小是会变的，所以i要从q.size()开始从大往小减
                TreeNode* t = q.front();
                q.pop();
                oneLevel.push_back(t->val);
                if(t->left) q.push(t->left);
                if(t->right) q.push(t->right);
            }
            res.push_back(oneLevel);
        }
        return res;
    }
};

 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        if(!root) 
            return {};
        vector<vector<int>> res;
        queue<TreeNode* > q{{root}};
        while(!q.empty()){
            vector<int> oneLevel;
            for(int i = q.size(); i>0; i--){
                TreeNode* t = q.front();
                q.pop();
                oneLevel.push_back(t->val);
                if(t->left) q.push(t->left);
                if(t->right) q.push(t->right);
            }
            res.insert(res.begin(), oneLevel);    //倒序插入
        }
        return res;
    }
};

 

之形的意思是：第0行是从左到右遍历，第1行是从右到左遍历，以此类推，交叉往返的之字形的层序遍历。

这里需要注意的一点是：不能将某一层的左子树和右子树逆序插入，这样会导致下一层的顺序出错。而是应该在奇数层时将各个结点反向插入

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        vector<vector<int> > res;
        if(!root)
            return {};
        queue<TreeNode* > q{{root}};
        int j = 0;   //层数从0开始计数
        while(!q.empty()){
            vector<int> oneLevel;
            for(int i=q.size(); i>0; i--){
                TreeNode* t = q.front();
                q.pop();
                
                if(j%2 == 0){
                    oneLevel.push_back(t->val);     //偶数层正向插入
                }
                else{
                    oneLevel.insert(oneLevel.begin(), t->val);   //奇数层时反向插入
                }  
                if(t->left) q.push(t->left);
                if(t->right) q.push(t->right);
            }
            j++;
            res.push_back(oneLevel);
        }
        return res;
    }
};

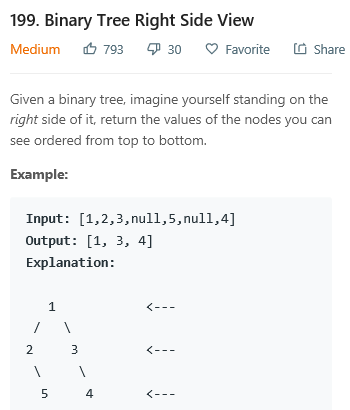
即打印出二叉树每一行最右边的一个结点。使用队列来实现，遍历每层的结点时，把下一层的结点都存入队列中，则每当开始新一层结点的遍历之前，先把新一层最后一个结点值存到res中。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        vector<int> res;
        if(!root) return {};
        queue<TreeNode*> q{{root}};
        while(!q.empty()){
            res.push_back(q.back()->val);   //将每层的最后一个结点保存到res中
            for(int i=q.size(); i>0; i--){
                TreeNode* t = q.front();
                q.pop();
                if(t->left) q.push(t->left);
                if(t->right) q.push(t->right);
            }
        }
        
        return res;
    }
};