动态规划 leetcode 343,279,91 & 639. Decode Ways,62,63,198


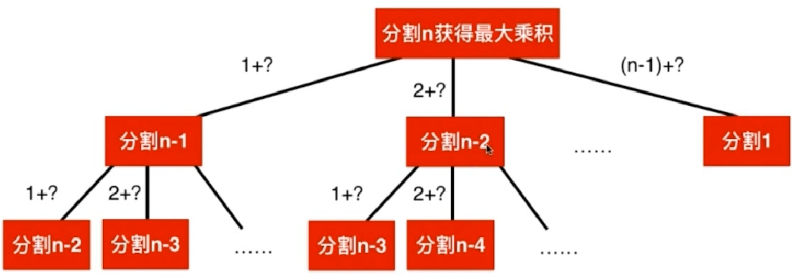
最优子结构:通过求子问题的最优解,可以获得原问题的最优解。
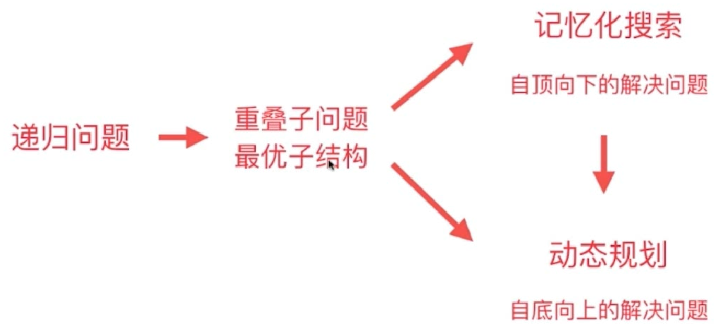
解法一:记忆化搜索
class Solution { private: vector<int> memo; int max3(int a, int b, int c){ return max(a, max(b,c)); } int breakInteger(int n){ //将n进行分割(至少分割两部分),可以获得的最大乘积 if(n == 1) return 1; //终止条件 if(memo[n]!= -1) return memo[n]; int res = -1; for(int i=1;i<=n-1;i++){ //i + (n-i) res = max3(res, i*(n-i), i * breakInteger(n-i)) ; memo[n] = res; } return res; } public: int integerBreak(int n) { //n为传入的数 memo = vector<int>(n+1,-1); //初始化为n+1个-1 return breakInteger(n); } };
解法二:动态规划
class Solution { private: vector<int> memo; int max3(int a, int b, int c){ return max(a, max(b,c)); } int breakInteger(int n){ //memo[i]将数字i进行分割(至少分割两部分),可以获得的最大乘积 vector<int> memo(n+1,-1); memo[1] = 1; for(int i=2;i<=n;i++){ //求解memo[i] for(int j=1; j<=i-1;j++){ // j + (i-j) memo[i] = max3(memo[i], j*(i-j), j*memo[i-j]); //j*(i-j) 表明不必继续分了 } } return memo[n]; } public: int integerBreak(int n) { //n为传入的数 memo = vector<int>(n+1,-1); //初始化为n+1个-1 return breakInteger(n); } };


思路:如下图所示,红色部分表示平方数,所有的完美平方数都可以看做一个普通数加上一个完美平方数,那么递推式就变为了:dp[i + j * j] = min(dp[i] + 1, dp[i + j * j]),dp[]存储的是最少的平方数。

class Solution { public: int numSquares(int n) { vector<int> dp(n+1, INT_MAX); for(int i=0;i*i<=n;i++){ dp[i*i] = 1; } for(int i=1; i<=n;i++){ for(int j=1;i+j*j <=n; j++){ dp[i+j*j] = min(dp[i]+1, dp[i+j*j]); } } return dp[n]; } };


输入:非空,只包含数字的字符串;
输出:能够被解码的总共方式。
思路类似爬楼梯
class Solution { public: int numDecodings(string s) { // s[0]=='0' 代表字符串开头为0 需要return 0 if(s.empty() || (s.size()>1 && s[0]=='0') ) return 0; int n = s.size(); vector<int> dp(n+1, 0); dp[0] = 1; for(int i=1;i<dp.size();i++){ //s数组的下标从0开始,相应的dp从1开始 dp[i] = (s[i-1] == '0') ? 0 : dp[i-1]; //只考虑一位的情况 if(i>1 && (s[i-2]=='1' || (s[i-2]=='2' && s[i-1]<='6') ) ) //当十位数为1时,个位数可以任意取值;而十位数为2时,个位数只能取从0-6的数 dp[i] += dp[i-2]; // dp[i] = dp[i-1] + dp[i-2] } return dp.back(); } };
class Solution { public: int numDecodings(string s) { //上楼梯问题的变种: DP //f[i] = f[i-1](when s[i]!=0) + f[i-2](when s[i-1]s[i]组成的数字在10-26之间) int n = s.size(); vector<int> f(n+1, 0); f[0] = 1; for(int i=1; i<=n; i++){ if(s[i-1] != '0') f[i] += f[i-1]; if(i>=2 && s[i-2]!='0' && (s[i-2]-'0')*10 + (s[i-1]-'0') <= 26) f[i] += f[i-2]; } return f[n]; // return f[1] = 0 if s = "0" } };
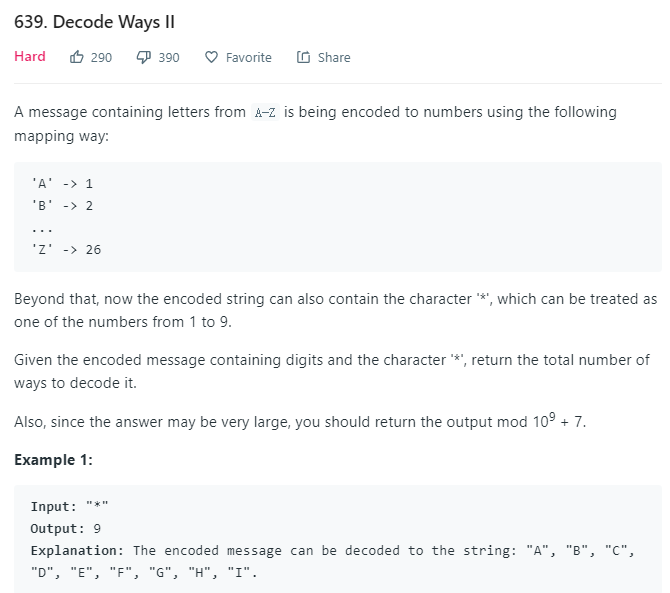
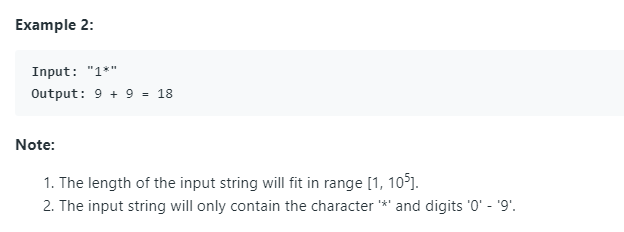
参考链接:https://zxi.mytechroad.com/blog/dynamic-programming/leetcode-639-decode-ways-ii/
class Solution { public: static const long Kmod = 1e9 + 7; int numDecodings(string s) { // * = 9 [1-9] // A = 1 if 1 <= A <= 26 // A = 0 if A = 0 // *A = 2 [1-2] if 0 <= A <= 6 // *A = 1 if A > 6 // A* = 9 [11-19] if A = 1 // A* = 6 [21-26] if A = 2 // ** = 15 [11-19, 21-26] int n = s.size(); vector<long> dp(n+1, 0); dp[0] = 1; //代表空串为1 dp[1] = ways(s[0]); //s的前1个元素 for(int i=2; i<=n; i++){ dp[i] = ways(s[i-1])*dp[i-1] + ways(s[i-2], s[i-1])*dp[i-2]; dp[i] %= Kmod; } return dp[n]; } int ways(char c){ if(c == '0') return 0; if(c == '*') return 9; return 1; } int ways(char c1, char c2){ if(c1 == '*' && c2 == '*') return 15; else if(c1 == '*'){ if(c2>='0' && c2<='6') return 2; return 1; } else if(c2 == '*'){ if(c1 == '1') return 9; else if(c1 == '2') return 6; } else { int prefix = (c1 -'0')*10 + (c2 -'0'); if( prefix >= 10 && prefix <= 26) return 1; } return 0; } };
滚动数组优化空间:
class Solution { public: static const long Kmod = 1e9 + 7; int numDecodings(string s) { // * = 9 [1-9] // A = 1 if 1 <= A <= 26 // A = 0 if A = 0 // *A = 2 [1-2] if 0 <= A <= 6 // *A = 1 if A > 6 // A* = 9 [11-19] if A = 1 // A* = 6 [21-26] if A = 2 // ** = 15 [11-19, 21-26] int n = s.size(); //滚动数组优化空间 vector<long> dp(2, 0); dp[0] = 1; //代表空串为1 dp[1] = ways(s[0]); //s的前1个元素 for(int i=2; i<=n; i++){ long dp_i = ways(s[i-1])*dp[1] + ways(s[i-2], s[i-1])*dp[0]; dp_i %= Kmod; dp[0] = dp[1]; dp[1] = dp_i; } return dp[1]; } int ways(char c){ if(c == '0') return 0; if(c == '*') return 9; return 1; } int ways(char c1, char c2){ if(c1 == '*' && c2 == '*') return 15; else if(c1 == '*'){ if(c2>='0' && c2<='6') return 2; return 1; } else if(c2 == '*'){ if(c1 == '1') return 9; else if(c1 == '2') return 6; } else { int prefix = (c1 -'0')*10 + (c2 -'0'); if( prefix >= 10 && prefix <= 26) return 1; } return 0; } };
62

递推式:dp[i][j] = dp[i-1][j] + dp[i][j-1];
class Solution { public: int uniquePaths(int m, int n) { int dp[m][n]; dp[0][0] = 1; for(int i=1;i<m;i++) dp[i][0] = 1; for(int i=1;i<n;i++) dp[0][i] = 1; for(int i=1;i<m;i++){ for(int j=1;j<n;j++) dp[i][j] = dp[i-1][j] + dp[i][j-1]; } return dp[m-1][n-1]; } };
63

思路:当遇到为1的点时,将该位置的dp数组的值清零。
注意:再做这道题的时候,int型的dp数组已经不能通过所有测试用例了,报错信息:

说明 dp[i][j] = dp[i-1][j] + dp[i][j-1] 超出了int型的最大范围,故需要将dp数组定义为long型。
class Solution { public: int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) { int m = obstacleGrid.size(), n = obstacleGrid[0].size(); if(m==0 || n==0 || obstacleGrid[0][0]==1) return 0; long dp[m][n]; dp[0][0] = 1; for(int i=1; i<m; ++i){ dp[i][0] = (obstacleGrid[i][0] ==1)? 0:dp[i-1][0]; } for(int i=1; i<n; ++i){ dp[0][i] = (obstacleGrid[0][i] ==1)? 0:dp[0][i-1]; } for(int i=1; i<m; ++i) for(int j=1; j<n; ++j) dp[i][j] = (obstacleGrid[i][j] ==1)? 0: dp[i-1][j] + dp[i][j-1]; return dp[m-1][n-1]; } };
class Solution { public: int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) { if(obstacleGrid.empty() || obstacleGrid[0].empty() || obstacleGrid[0][0]==1) return 0; int m = obstacleGrid.size(); int n = obstacleGrid[0].size(); int dp[m][n]; for(int i=0;i<m;i++){ for(int j=0;j<n;j++){ if(obstacleGrid[i][j] == 1) dp[i][j] = 0; else if(i==0 && j==0) dp[i][j] = 1; else if(i==0 && j>0) dp[i][j] = dp[i][j-1]; else if(i>0 && j==0) dp[i][j] = dp[i-1][j]; else dp[i][j] = dp[i-1][j] + dp[i][j-1]; } } return dp[m-1][n-1]; } };



解法一:自顶向下:
class Solution { private: //memo[i]表示考虑去抢劫nums[i...n)所能获得的最大收益 vector<int> memo; //考虑抢劫 nums[index...nums.size()] 这个范围的所有房子 int tryRob(vector<int> &nums, int index){ if(index >= nums.size()) //空集 return 0; if(memo[index] != -1) return memo[index]; int res = 0; for(int i=index; i<nums.size();i++){ res = max(res, nums[i] + tryRob(nums, i+2)); } memo[index] = res; return res; } public: int rob(vector<int>& nums) { memo = vector<int>(nums.size(), -1); return tryRob(nums, 0); } };
解法二:动态规划


 浙公网安备 33010602011771号
浙公网安备 33010602011771号