(归并和快排) lintcode 399
1. 我们知道它们都使用了分治算法:将原问题分割成同等结构的子问题,子问题解决后,原问题也得到了解决。
衍生出来的问题:
1)逆序对:
对应题目:
剑指:数组中的逆序对,在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007。
如下图:23是正序对,而21是逆序对

解法一: 暴力解法,考察每一个数对。算法复杂度:O(n^2)
解法二:归并排序的思路来求逆序对的个数。算法复杂度:O(nlogn)
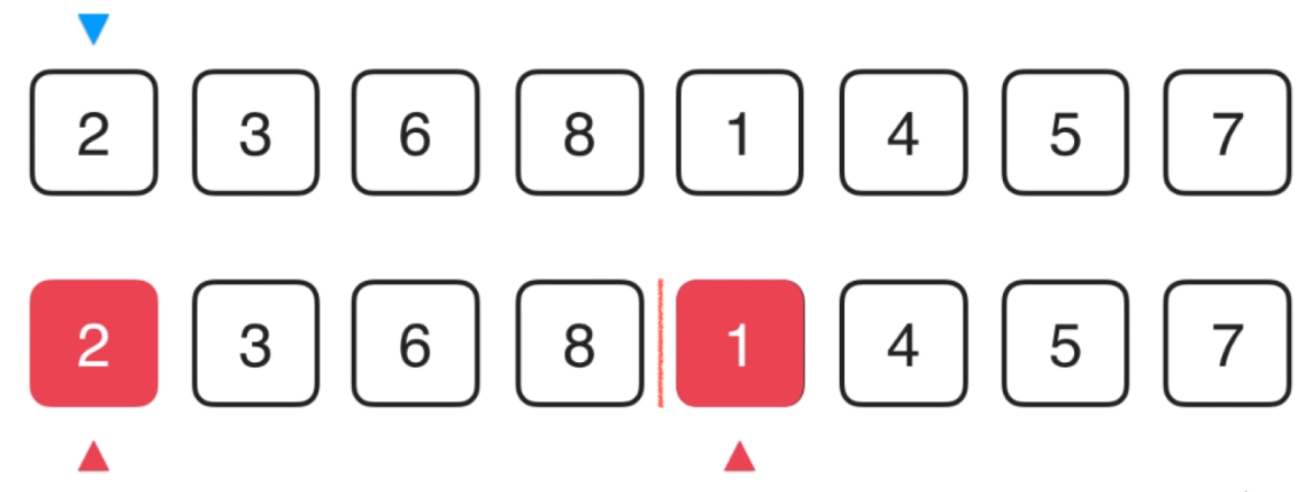
假设正在归并上面的数组,左侧的2,3,6,8和右侧的1,4,5,7已经排好序了,左侧和右侧内部都没有逆序对,而从左侧取一个数,从右侧取一个数,则有可能形成逆序对。
例如,开始左侧拿出2,右侧拿出1,可知2>1,形成了逆序对。此时逆序对只是加1吗?并不是,因为2右边的数都是大于2的,所以可以判断左边的数和右边的1可以形成4对逆序对((2,1)、(3,1)、(6,1)、(8,1))。
接下来比2和4,不会形成逆序对。再比3和4,不会形成逆序对。
当比较到6和4的时候,形成了逆序对,个数为2((6,4)、(8,4))。

归纳一下,也就是在归并的时候,如果右侧的元素小于左侧的元素,这个时候开始统计逆序对就行了,如果左侧的索引为i,左侧的末尾元素的索引为mid,逆序对个数就为mid-i+1。
这样并没有结束,前面的假设是左侧和右侧是有序的,事实上并不是,左侧和右侧也进行了归并的过程才能变得有序,而在归并过程中,也能计算出逆序对的个数。
所以:
总的逆序对的个数=左侧归并时求得的逆序对个数 + 右侧归并时求得的逆序对个数 + 对整体进行归并时的逆序对个数。
注意:这三种情况是没有重复的。左侧归并找到的逆序对相当于从左侧数组中取2个数,而整体归并的时候是分别从左右数组中取1个数,所以不可能发生重复!
#define div 1000000007 class Solution { public: int InversePairs(vector<int> data) { int n = data.size(); vector<int> aux(data); //辅助空间 return mergeSort(data, aux, 0, n-1); } int mergeSort(vector<int> &arr, vector<int> &aux, int l, int r){ if(l>=r) return 0; int mid = (l+r)/2; int left = mergeSort(arr, aux, l , mid)% div ; //统计左部分逆序数的个数 int right = mergeSort(arr, aux, mid+1, r)% div; //统计右部分逆序数的个数 return (left + right + merge(arr, aux, l , mid, r)) % div; //左+右+全体 } int merge(vector<int> &arr, vector<int> &aux, int l, int mid, int r){ for( int i = l ; i <= r; i ++ ) aux[i] = arr[i]; int res = 0; //统计逆序对的数量 //初始化,i指向左半部分的起始索引位置l,j指向右半部分起始索引位置mid+1 int i = l, j = mid+1; for(int k = l; k<=r; k++){ if(i>mid){ //左部分已经遍历完,还剩下右部分 arr[k] = aux[j]; j++; } else if(j>r){ arr[k] = aux[i]; i++; } else if(aux[i]<aux[j]){ arr[k] = aux[i]; i++; } else{ //当左部分的aux[i]>aux[j],此时下标从i到mid与此时的aux[j]都组成了逆序对 arr[k] = aux[j]; j++; res += (mid - i +1); res %= div; } } return res; } };


参考链接:https://www.jiuzhang.com/solution/nuts-bolts-problem/#tag-other-lang-cpp
/** * class Comparator { * public: * int cmp(string a, string b); * }; * You can use compare.cmp(a, b) to compare nuts "a" and bolts "b", * if "a" is bigger than "b", it will return 1, else if they are equal, * it will return 0, else if "a" is smaller than "b", it will return -1. * When "a" is not a nut or "b" is not a bolt, it will return 2, which is not valid. */ class Solution { public: /** * @param nuts: a vector of integers * @param bolts: a vector of integers * @param compare: a instance of Comparator * @return: nothing */ void sortNutsAndBolts(vector<string> &nuts, vector<string> &bolts, Comparator compare) { quick_sort(0, nuts.size()-1, nuts, bolts, compare); } void quick_sort(int start, int end, vector<string>& nuts, vector<string>& bolts, Comparator compare){ if(start >= end) return; int pivotN = (start + end)/2; //取nuts中点作为pivot int pivotB; for(int i=start; i<=end; i++){ //在bolts中遍历找出和nuts[pivotN]对应的字符 if(compare.cmp(nuts[pivotN], bolts[i]) == 0){ pivotB = i; break; } } //将找到的pivot与start位置对应的字符交换 swap(nuts[pivotN], nuts[start]); swap(bolts[pivotB], bolts[start]); //quick sort Nuts And Bolts int i = start+1, j = end; if(i==j) return; while(i<=j){ if(compare.cmp(nuts[i], bolts[start]) < 0){ i++; continue; //找到一个大于nuts[start]的元素 } if(compare.cmp(nuts[j], bolts[start]) > 0){ j--; continue; } swap(nuts[i], nuts[j]); i++; j--; } i = start+1, j = end; while(i<=j){ if(compare.cmp(nuts[start], bolts[i]) > 0){ i++; continue; } if(compare.cmp(nuts[start], bolts[j]) < 0){ j--; continue; } swap(bolts[i], bolts[j]); i++; j--; } quick_sort(start, j, nuts, bolts, compare); quick_sort(i, end, nuts, bolts, compare); } };



