快速排序,三路快排
时间复杂度O(nlongn)
基本思想:取一个枢纽值(privot),将剩余数组的值依次与privot进行比较,若比privot大就放在privot左边;若小就放在右边。
基础版:假设数组左边界下标为l,右边界下标为r,将下标l所在的元素值记为privot,使得 arr[l+1...j]<v ; arr[j+1...i)>v ,i是当前要考察的元素。遍历数组完成后将arr[j]与arr[l]交换位置。
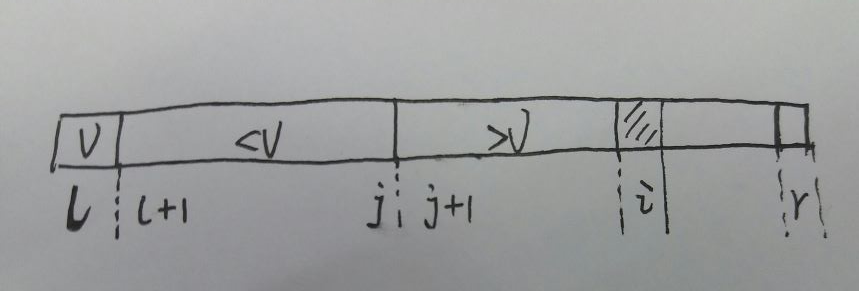
template<typename T> //泛型 //对arr[l...r]部分进行快速排序 //返回p,使得arr[l...p-1]<arr[p]; arr[p+1...r]>arr[p] int _partition(T arr[], int l, int r){ T v = arr[l]; //设定pivot值 //arr[l+1...j]<v ; arr[j+1...i)>v i是当前要考察的元素,所以是开区间 int j = l; for(int i=l+1;i<=r;i++){ if(arr[i] < v){ swap(arr[j+1], arr[i]); j++ } } swap(arr[l], arr[j]); return j; } void _quickSort(T arr[], int l, int r){ if(l>=r) return; int p = _partition(arr,l,r); quickSort(arr, l, p-1); quickSort(arr, p+1,r); }
void quickSort(T arr[], int n){
_quickSort(arr, 0, n-1);
}
优化方法一:将递归底层的处理改为插入排序进行优化。
template<typename T> //泛型 //对arr[l...r]部分进行快速排序 //返回p,使得arr[l...p-1]<arr[p]; arr[p+1...r]>arr[p] int _partition(T arr[], int l, int r){ T v = arr[l]; //设定pivot值 //arr[l+1...j]<v ; arr[j+1...i)>v i是当前要考察的元素,所以是开区间 int j = l; for(int i=l+1;i<=r;i++){ if(arr[i] < v){ 将j+1所指的大于v的元素与arr[i]交换 swap(arr[j+1], arr[i]); j++ } } swap(arr[l], arr[j]); return j; } void _quickSort(T arr[], int l, int r){ //if(l>=r) //return; if(r-l<=15){ insertionSort(arr,l,r); return; } int p = _partition(arr,l,r); quickSort(arr, l, p-1); quickSort(arr, p+1,r); }
void quickSort(T arr[], int n){
_quickSort(arr, 0, n-1);
}
优化方法二:
对于近乎有序的数组,快速排序比归并排序慢了太多。因为快排所生成的递归树不平衡,它可能比log(n)还要高。最差的情况是:当数组近乎有序时,递归树的高度是n,时间复杂度会达到O(n^2)。
可改进为:随机选择一个元素作为privot,而不是选择第一个点
// 对arr[l...r]部分进行partition操作 // 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p] template <typename T> int _partition(T arr[], int l, int r){ // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot swap( arr[l] , arr[rand()%(r-l+1)+l] ); T v = arr[l]; int j = l; for( int i = l + 1 ; i <= r ; i ++ ) if( arr[i] < v ){ j ++; swap( arr[j] , arr[i] ); } swap( arr[l] , arr[j]); return j; } // 对arr[l...r]部分进行快速排序 template <typename T> void _quickSort(T arr[], int l, int r){ // 对于小规模数组, 使用插入排序进行优化 if( r - l <= 15 ){ insertionSort(arr,l,r); return; } int p = _partition(arr, l, r); _quickSort(arr, l, p-1 ); _quickSort(arr, p+1, r); } template <typename T> void quickSort(T arr[], int n){ srand(time(NULL)); _quickSort(arr, 0, n-1); }
所使用的插入排序代码:
// 对arr[l...r]范围的数组进行插入排序 template<typename T> void insertionSort(T arr[], int l, int r){ for( int i = l+1 ; i <= r ; i ++ ) { T e = arr[i]; int j; for (j = i; j > l && arr[j-1] > e; j--) arr[j] = arr[j-1]; arr[j] = e; } return; }
优化方法三:当数组中出现大量相同的值时,Partition可能将数组分成极度不平衡的两部分,就会退化成为一个O(n^2)级别的算法。
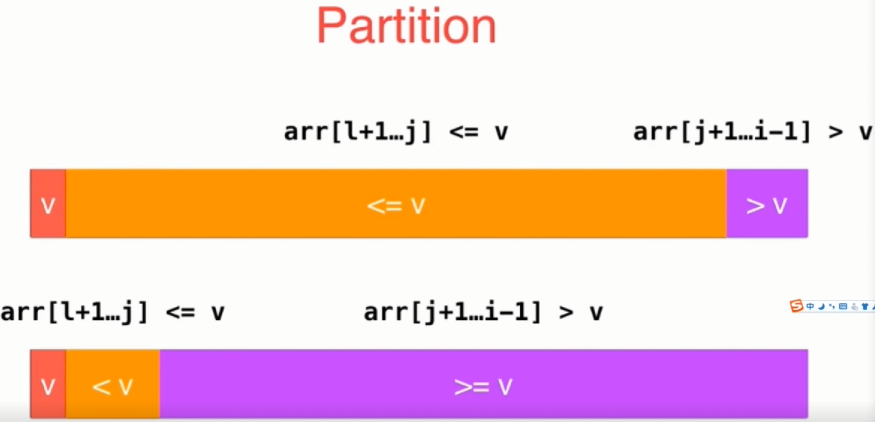
改进方法:从数组两端往中间扫描
1)
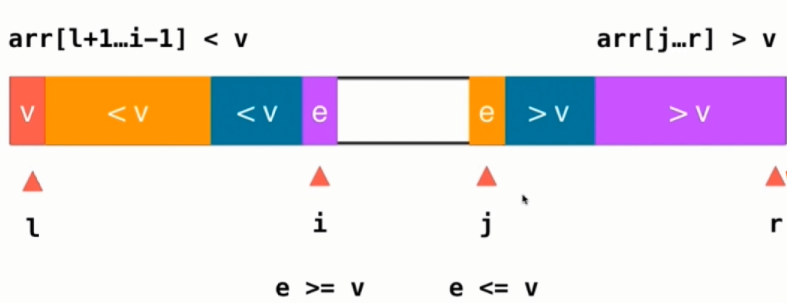
2) 当左边扫描到的arr[i]>v时停止;当右边扫描到的arr[j]<v时停止
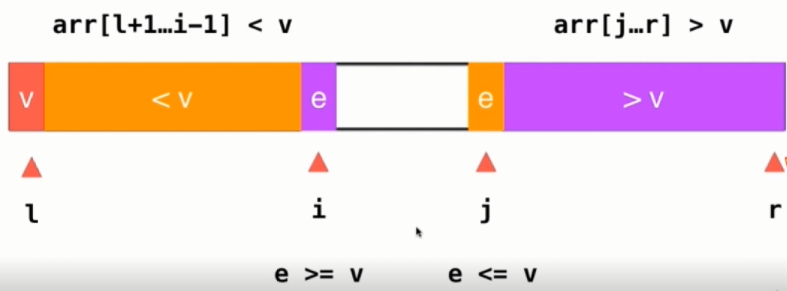
3) 交换i和j所指元素
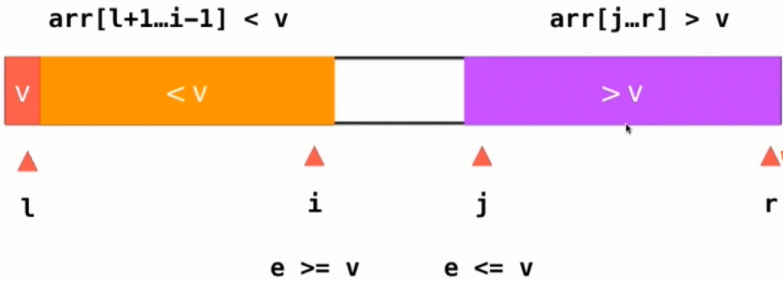
4) 当i和j指向的都是等于v的元素时,也要交换位置,这样可以避免有大部分的等于v的元素集中在某一部分的情况。
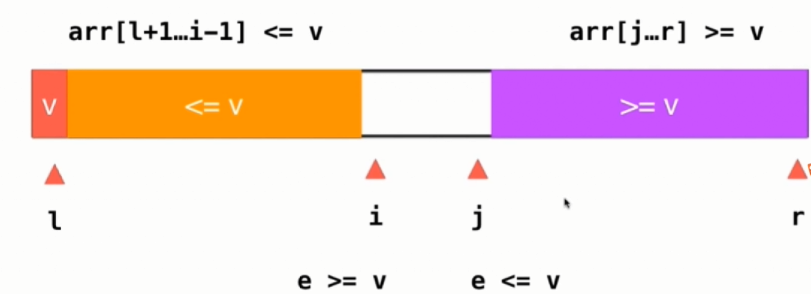
template<typename T> //泛型 //对arr[l...r]部分进行快速排序 //返回p,使得arr[l...p-1]<arr[p]; arr[p+1...r]>arr[p] int _partition(T arr[], int l, int r){ swap(arr[l],arr[rand()%(r-l+1)+l]); T v = arr[l]; //设定最左边的元素为pivot值 //arr[l+1...i)<=v ; arr(j...r]>=v i是当前要考察的元素,所以是开区间 int i=l+1,j=r; //初始定义下,区间为空 while(true){ while(i<=r && arr[i]<v) i++; while(j>=l+1 && arr[j]>v) j--; if(i>j) break; swap(arr[i], arr[j]); i++; j--; } //j指向的是从右边开始最后一个小于v的元素,将它与标定点交换 swap(arr[l], arr[j]); return j; } void _quickSort(T arr[], int l, int r){ if(r-l<=15){ insertionSort(arr,l,r); return; } int p = _partition(arr,l,r); _quickSort(arr, l, p-1); _quickSort(arr, p+1,r); } void quickSort(T arr[], int n){ //设置随机种子 srand(time(NULL)); _quickSort(arr, 0, n-1); }
对于为什么是while(i<=r && arr[i]<v) i++; 而不是while(i<=r && arr[i]<=v) i++; 的一点思考 :
因为多了个等号的判断使得如果有大量重复的值时,会造成两棵子树不平衡。
三路快排:用于给有大量重复元素进行排序
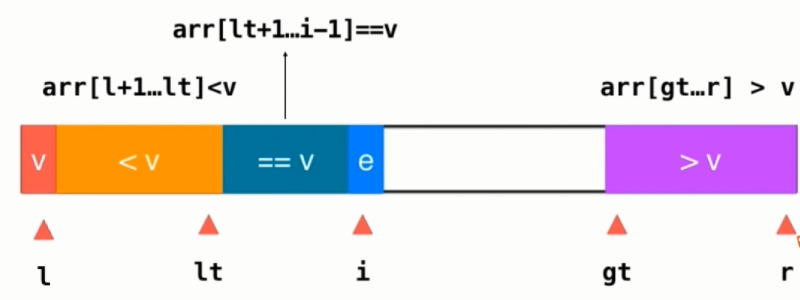
//三路快速排序处理arr[l...r] //将arr[l...r]分为<v ;==v ; >v 三部分 //之后递归对<v ; >v 两部分继续进行三路快速排序 template<typename T> //泛型 void _quickSort3Ways(T arr[], int l, int r){ if(r-l<=15){ insertionSort(arr,l,r); return; } //partion swap(arr[l],arr[rand()%(r-l+1)+l); //将随机生成的下标所代表的元素与最左边的元素交换 T v = arr[l]; //设置最左侧元素为privot int lt = l; //arr[l+1...lt]<v int gt = r+1; //arr[gt...r]>v int i = l+1; //arr[lt+1...i) == v while(i<gt){ if(arr[i]<v){ swap(arr[i], arr[lt+1]); lt++; i++; } else if(arr[i]>v){ swap(arr[i], arr[gt-1]); gt--; } else //arr[i] == v i++; } swap(arr[l], arr[lt]); _quickSort3Ways(arr,l,lt-1); _quickSort3Ways(arr,gt,r); } void quickSort3Ways(T arr[], int n){ //设置随机种子 srand(time(NULL)); _quickSort3Ways(arr, 0, n-1); }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号