【算法】【快慢指针】环形链表问题--力扣两道经典题目讲解【超详细保姆级别教程】
【算法】【快慢指针】环形链表问题–力扣两道经典题目讲解【超详细保姆级别教程】
先赞后看好习惯 打字不容易,这都是很用心做的,希望得到支持你 大家的点赞和支持对于我来说是一种非常重要的动力 看完之后别忘记关注我哦!️️️
这篇干货满满----建议本篇收藏后食用
【例题1】力扣141.环形链表
题目


算法及思路
这道题目其实写起来非常简单:我们使用一个双指针就可以解决,我们可以定义一个fast指针,定义一个slow指针,fast指针每一次走两步,slow指针每一次走一步。
显然,fast指针先进环,slow指针后进环,因为进了环之后fast指针总会追上slow指针,如果没有环,fast和slow走到尾都不会相等。
很明显这一题我们就做出来了,但是事实上真的有那么简单吗,其实里面还有一些原理我们还要探究。
如果我们在面试场上,面试官让我们写这道题的代码,相信已经学会的我们一分钟就能做出这道题。
如果面试官让我们证明为什么fast每次要走两步,slow每次走一步?我们应该如何应对?
如果fast每次走三步,走四步行不行?
答案是不行的。
试想,假设现在fast和slow都已经进环了,fast要开始追赶slow了,如果先按照我们原先的思路,fast每次走两步,slow每次走一步,那么每走一次,fast和slow之间的距离减少的是1,这个非常关键,这保证了fast和slow之间是不会相互错过的。
如果我们的fast每次走三步,slow每次走一步,这样的话在一些情况下,fast是会错过slow的,这就会导致问题出现,因此,我们必须保证,fast和slow的速度只能相差1。
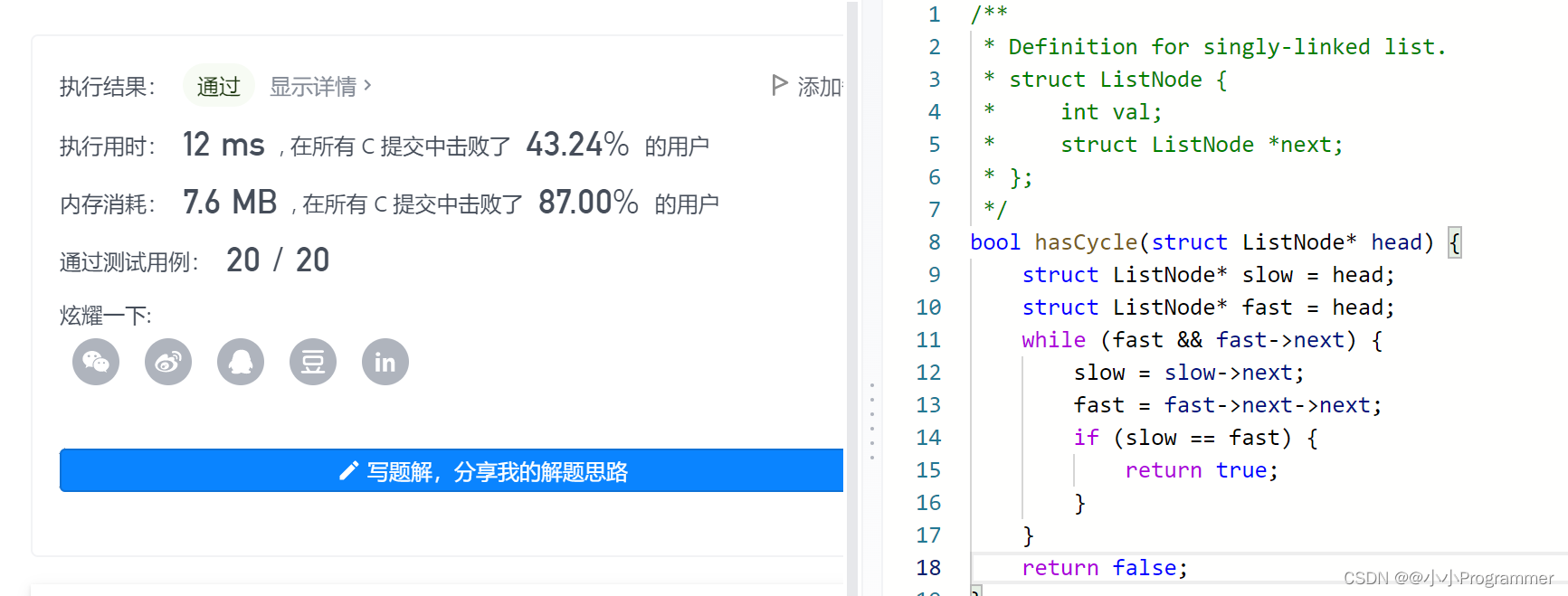
代码实现
bool hasCycle(struct ListNode* head) {
struct ListNode* slow = head;//慢指针
struct ListNode* fast = head;//快指针
while (fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
//如果进环之后,快指针迟早被慢指针追上
if (slow == fast) {
return true;
}
}
return false;//如果出了循环,表示遇到了NULL,也就是没有环。
}
【例题2】力扣142.环形链表ll
题目
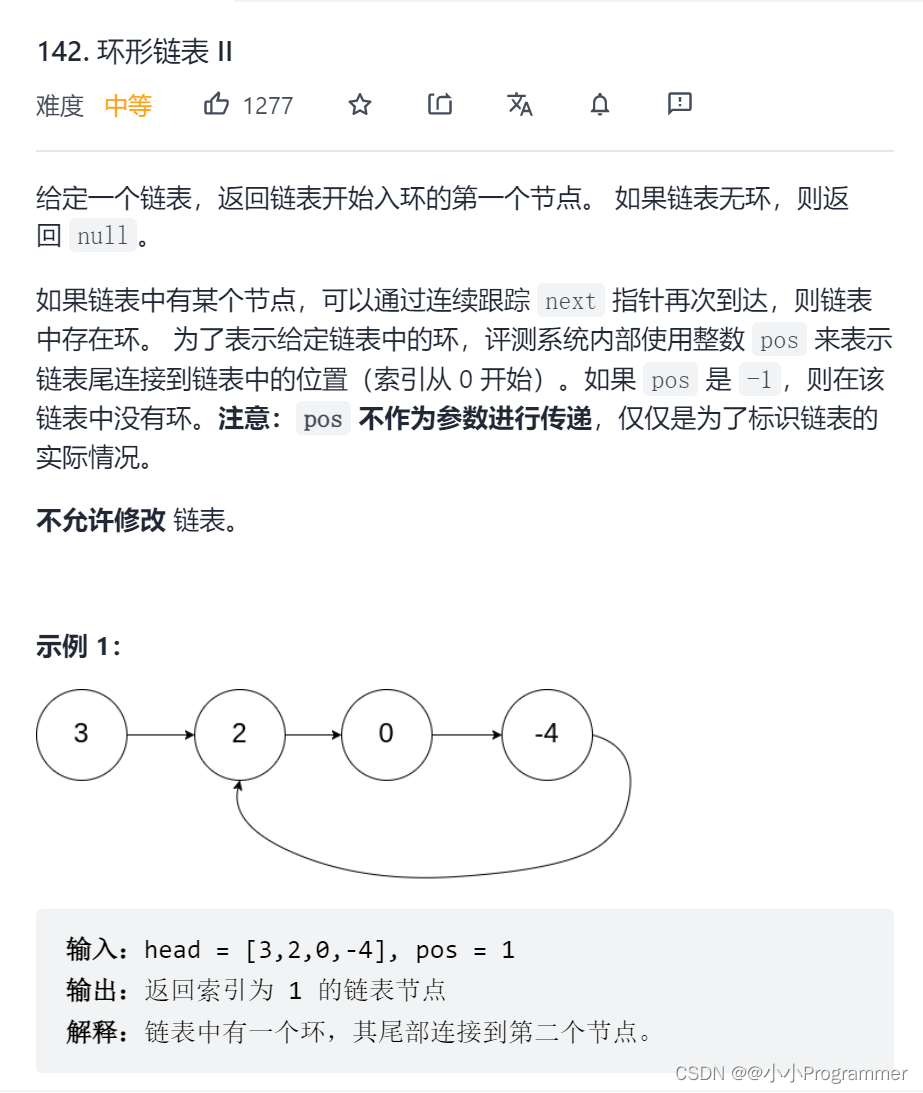

这道题跟上一道题看起来是差不多的,但是实现起来,还是较为复杂
此题在这里我提供两种思路供大家参考
思路一:
该思路较为简单,但是代码写起来比较的长。
实现过程:
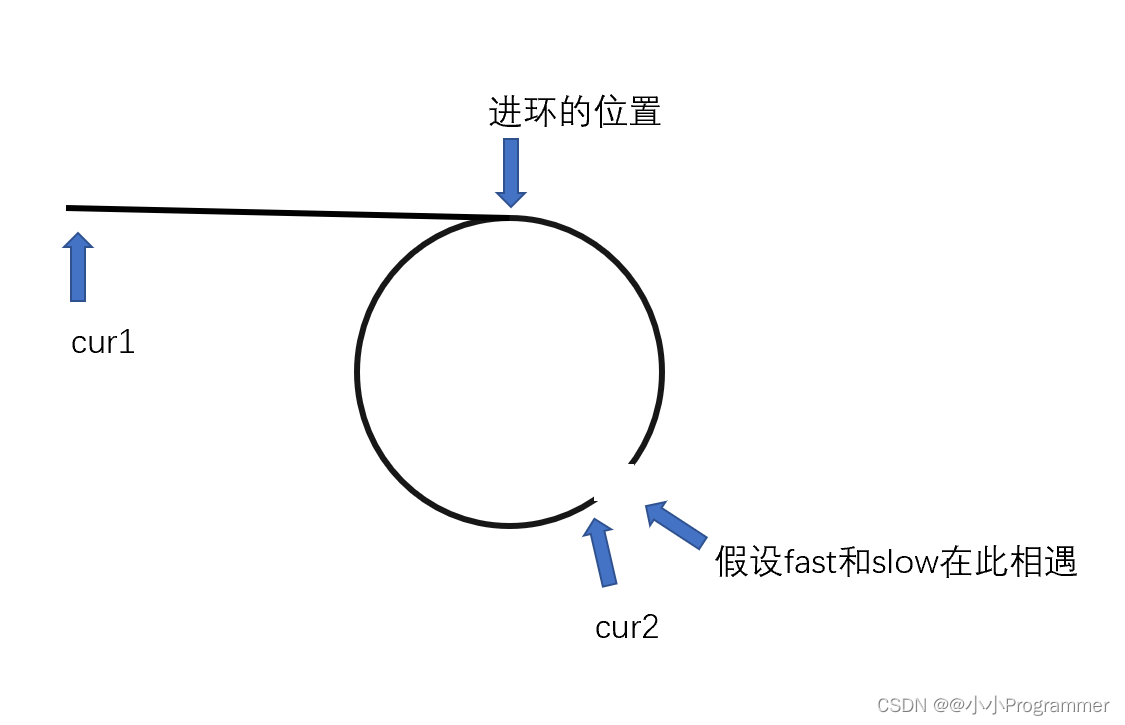
一开始与上一题相似,我们先用快慢指针,当快指针和慢指针相等的时候,记录该位置,并断开。如图:
这样我们就得到了两个相交链表。
我们就把这个问题转化为了相交链表找交点的问题。
有关于相交链表找交点的方法我在这里就不赘述了,这不属于环形链表的问题。
如果对相交链表找交点存在疑问的伙伴可以私信我,如果提该问题的人较多,我将会单独写一篇关于链表相交问题的博客供大家食用。
思路二:
该思路的思想证明过程较为复杂,但是代码非常的简洁。
分析过程:
思路2:写起来简单,需要公式证明,并且理解起来复杂
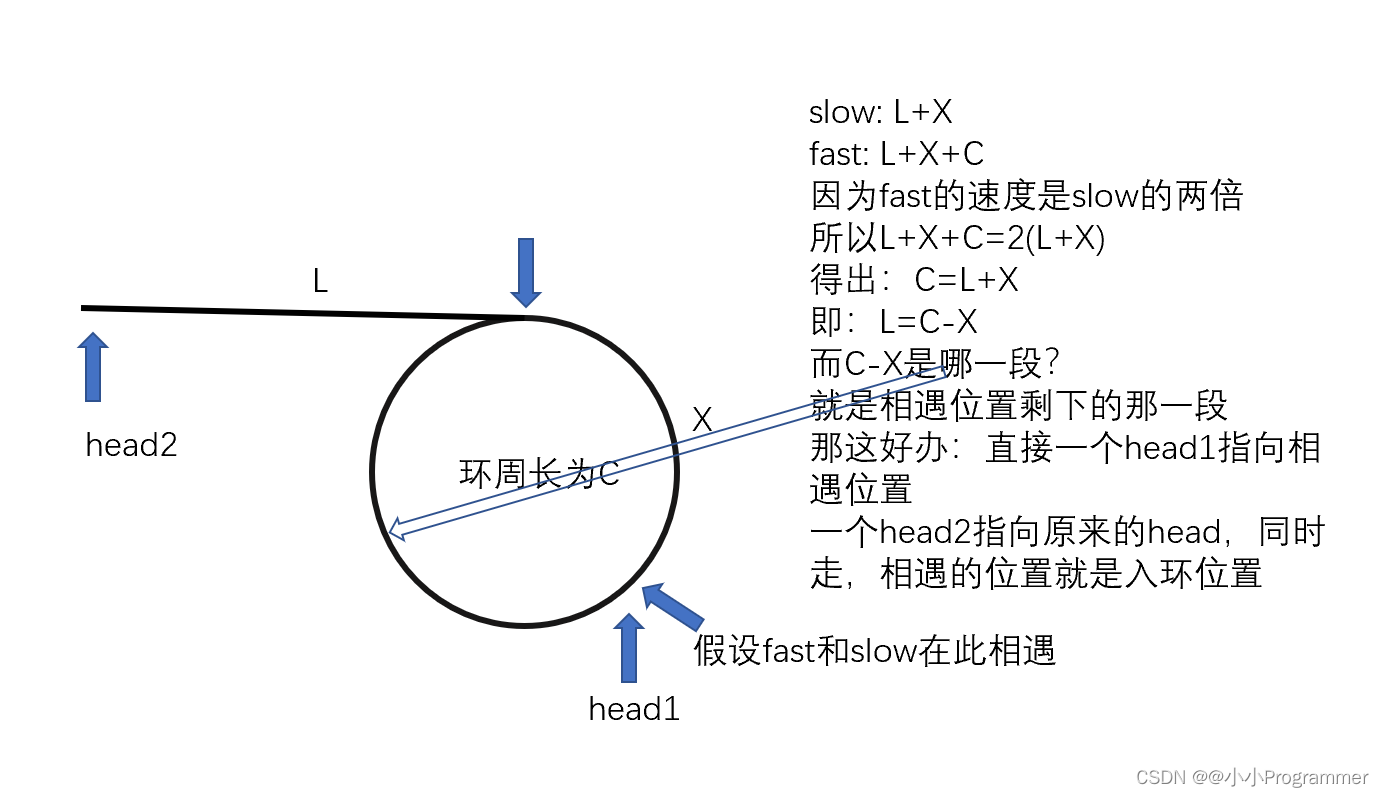
假设:head->pos的距离是L
pos->fast&&slow的交点是X
环的周长是C
相遇的时候:
慢指针走了:L+X,-----有伙伴问:有没有可能套了圈才相遇,不可能,因为速度只差1
这个时候很多伙伴会说:快指针走了:L+X+C–>这个结论可以推出,一个指针从相遇点开始走,一个指针从head开始走,会在pos相遇。如图所示:
虽然推出的结论是正确的,但是推导是错误的,为什么? 因为万一入环前的距离很长,会导致快指针走了不止一圈,慢指针才进来 因此–>正确的写法是
快指针走了:L+X+nC
所以得出:L=n*C-X
在此之前,fast可能已经走了n圈了
这才是正确的推导。
但是我们可以发现,我们得到的结论是一样的,因为head1是走了n圈之后,再和head2相遇。
思路一代码实现:
struct ListNode* detectCycle(struct ListNode* head) {
struct ListNode* fast = head;
struct ListNode* slow = head;
//快慢指针的相遇
while (fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
if (slow == fast) {
break;
}
}
//出来一定要判断是因为没有环而跳出的循环
//还是因为相遇了才跳出循环
if (head == NULL || head->next == NULL) {//如果只给了一个结点,光有下面那个判断条件是不够的。
return NULL;
}
if (fast != slow) {
return NULL;
}
//断开前后
struct ListNode* head2 = fast->next;
fast->next = NULL;
//转化为了一个链表相交问题
struct ListNode* head1 = head;
struct ListNode* cur1 = head1;
struct ListNode* cur2 = head2;
int l1 = 0;
int l2 = 0;
while (cur1) {
l1++;
cur1 = cur1->next;
}
while (cur2) {
l2++;
cur2 = cur2->next;
}
if (l2 > l1) {
for (int i = 0; i < l2 - l1; i++) {
head2 = head2->next;
}
}
else {
for (int i = 0; i < l1 - l2; i++) {
head1 = head1->next;
}
}
while (head1) {
if (head1 == head2) {
break;
}
head1 = head1->next;
head2 = head2->next;
}
return head1;
}
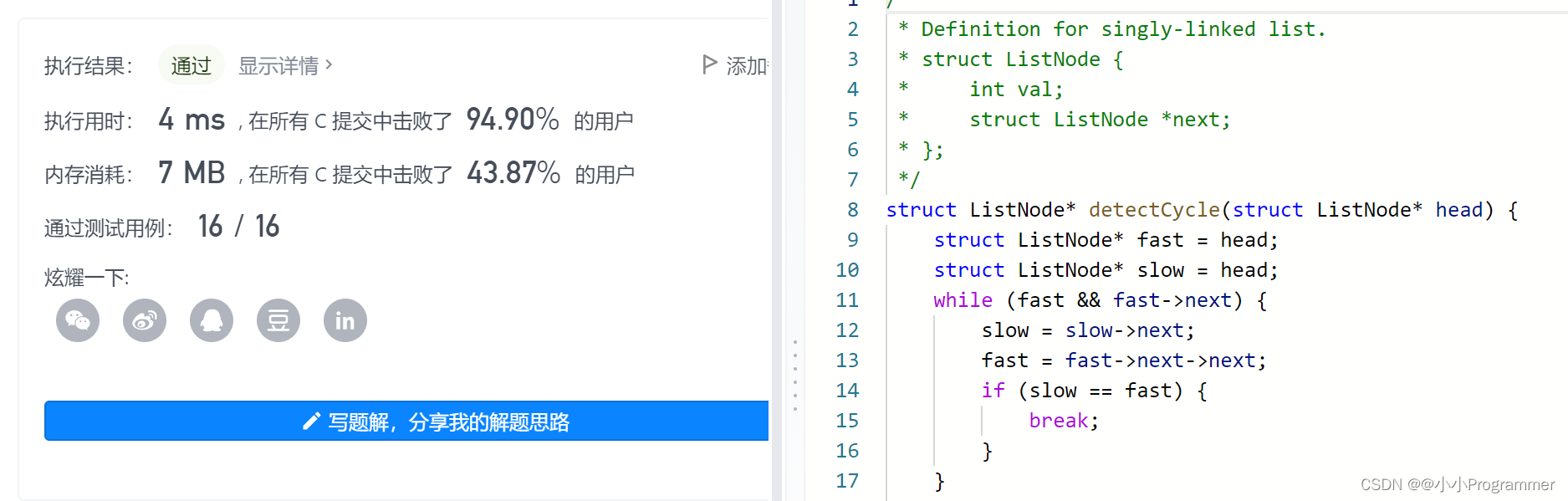
思路二代码实现:
struct ListNode* detectCycle(struct ListNode* head) {
struct ListNode* fast = head;
struct ListNode* slow = head;
//快慢指针找相遇
while (fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
if (slow == fast) {
break;
}
}
//如果只有一个结点,不能当成环了
if (head == NULL || head->next == NULL) {
return NULL;
}//直接返回空
if (fast != slow) {//如果只有一个结点的情况,这里也会满足!
return NULL;
}
//找入环点
struct ListNode* cur1 = head;
struct ListNode* cur2 = fast;
while (cur1 != cur2) {
cur1 = cur1->next;
cur2 = cur2->next;
}
return cur1;
}

尾声
以上就是今天环形链表两道经典题目和分析的全部内容,希望看完的小伙伴都可以有收获,如果对代码中一些细节的地方还是不明白的话,可以私信我。
在离开之前不要忘记点个赞点个收藏哦!