【算法】priority_queue在力扣题中的应用 | 力扣692 | 力扣347 | 力扣295 【超详细的注释和算法解释】
说在前面的话
博主也好长一段时间没有更新力扣的刷题系列了，今天给大家带来一些优先队列的经典题目，今天博主还是用C++给大家讲解，希望大家可以从中学到一些东西。
前言
那么这里博主先安利一下一些干货满满的专栏啦！
手撕数据结构
https://blog.csdn.net/yu_cblog/category_11490888.html?spm=1001.2014.3001.5482算法专栏https://blog.csdn.net/yu_cblog/category_11464817.html
STL源码剖析
https://blog.csdn.net/yu_cblog/category_11983210.html?spm=1001.2014.3001.5482
priority_queue 优先队列
优先队列的底层实现就是数据结构的堆。其中，小顶堆可以不断更新数组里的最小值，大顶堆可以不断更新数组里的最大值，push和pop自带排序功能，经常用来解决TopK问题。
如果大家有需要数据结构堆的实现可以通过博主的传送门食用噢~
【堆】数据结构-堆的实现【超详细的数据结构教学】https://blog.csdn.net/Yu_Cblog/article/details/124944614
692.前K个高频单词
看到频率，我们很自然可以想到哈希表，我们可以用哈希表记录每个单词出现的次数。看到前K个，可以断定这是一个topK问题，我们需要用到优先队列。但是，哈希表是单向的映射，因此我们还需要用到数据结构pair，这里博主自己实现了一个pair，整体代码如下：
class Pair {
public:
Pair(string e1, int e2)
:_e1(e1), _e2(e2) {}
string _e1;
int _e2;
bool operator<(const Pair& p) const
{
if (_e2 != p._e2)
return this->_e2 < p._e2;
//此时两个出现次数相等
return this->_e1 > p._e1;
}
};
struct cmp
{
bool operator()(const Pair& f1, const Pair& f2)
{
return f1 < f2;
}
};
class Solution {
private:
bool is_inArr(string s, vector<Pair>arr) {
for (int i = 0; i < arr.size(); i++) {
if (arr[i]._e1 == s)return true;
}
return false;
}
public:
vector<string> topKFrequent(vector<string>& words, int k) {
vector<string>ret;
unordered_map<string, int>hash;
for (int i = 0; i < words.size(); i++) {
++hash[words[i]];
}
vector<Pair>arr;
for (int i = 0; i < words.size(); i++) {
Pair tmp(words[i], hash[words[i]]);
if (!is_inArr(words[i], arr))
arr.push_back(tmp);
}
priority_queue<Pair, vector<Pair>, cmp>pq;
//初始化优先队列
for (int i = 0; i < arr.size(); i++) {
pq.push(arr[i]);
}
while (k--) {
Pair tmp = pq.top();
pq.pop();
ret.push_back(tmp._e1);
}
return ret;
}
};347.前K个高频元素
这题和上一题思路完全一样，这里直接给出代码：
class Pair {
public:
Pair(int e1, int e2)
:_e1(e1), _e2(e2) {}
int _e1;
int _e2;
bool operator<(const Pair& p) const
{
if (_e2 != p._e2)
return this->_e2 < p._e2;
//此时两个出现次数相等
return this->_e1 > p._e1;
}
};
struct cmp
{
bool operator()(const Pair& f1, const Pair& f2)
{
return f1 < f2;
}
};
class Solution {
private:
bool is_inArr(int s, vector<Pair>arr) {
for (int i = 0; i < arr.size(); i++) {
if (arr[i]._e1 == s)return true;
}
return false;
}
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
vector<int>ret;
unordered_map<int, int>hash;
for (int i = 0; i < nums.size(); i++) {
++hash[nums[i]];
}
vector<Pair>arr;
for (int i = 0; i < nums.size(); i++) {
Pair tmp(nums[i], hash[nums[i]]);
if (!is_inArr(nums[i], arr))
arr.push_back(tmp);
}
priority_queue<Pair, vector<Pair>, cmp>pq;
for (int i = 0; i < arr.size(); i++) {
pq.push(arr[i]);
}
while (k--) {
Pair tmp = pq.top();
pq.pop();
ret.push_back(tmp._e1);
}
return ret;
}
};295.数据流的中位数
比较容易想到的思路，用一个堆，取出中间的数：
class MedianFinder {
private:
priority_queue<int>pq;
public:
MedianFinder() {
}
void addNum(int num) {
pq.push(num);
}
double findMedian() {
priority_queue<int>pq_tmp = pq;
if (pq.size() % 2 == 0) {
for (int i = 0; i < pq.size() / 2 - 1; i++) {
pq_tmp.pop();
}
//现在接下来的两个就是要用的了
int num1 = pq_tmp.top();
pq_tmp.pop();
int num2 = pq_tmp.top();
pq_tmp.pop();
return (num1 + num2) / 2.0;
}
else {
for (int i = 0; i < pq.size() / 2; i++) {
pq_tmp.pop();
}
return pq_tmp.top();
}
}
};这个版本是无法通过的，虽然用了优先队列很大程度降低了时间复杂度，但是因为中间有拷贝过程，开销还是很大的，这样提交会超时。
用两个优先队列实现：
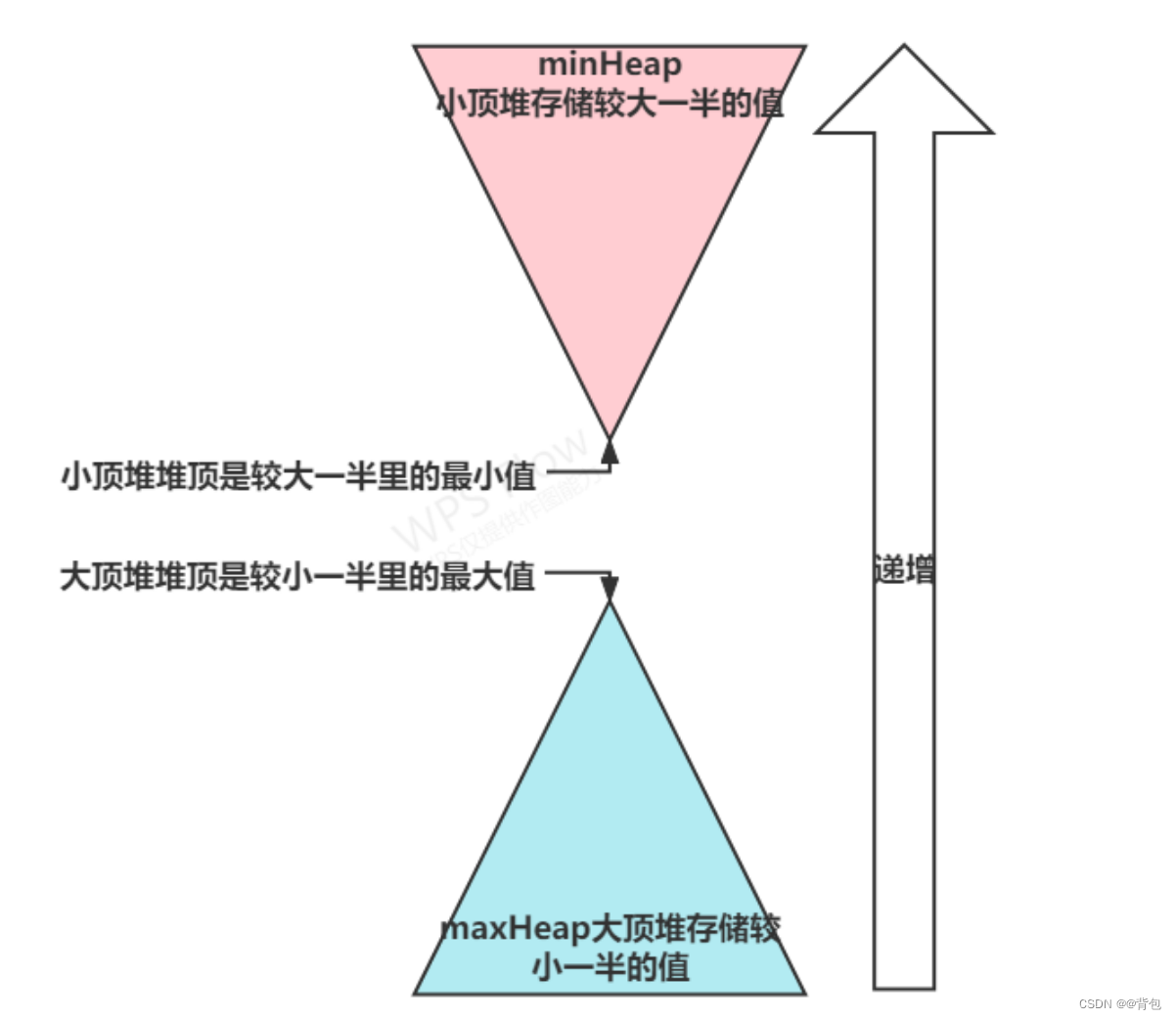
直接开两个堆
queMax记录比中位数大的 -- 是个小堆 -- 可以得到queMax的最小值
queMin记录比中位数小的 -- 是个大堆 -- 可以得到queMin的最大值
插入过程中保证 -- queMin的大小和queMax一样 或者queMin大小比queMax大小大1
如果queMin过大， 把其中最大的那个数插入到queMax中去
queMax过大同理
如果最后queMin.size()==queMax.size() 则中位数就是两个堆顶的平均
如果queMin.size()==queMax.size()+1 则中位数是queMin.top()
class MedianFinder {
public:
priority_queue<int, vector<int>, less<int>> queMin;
priority_queue<int, vector<int>, greater<int>> queMax;
MedianFinder() {}
void addNum(int num) {
if (queMin.empty() || num <= queMin.top()) {
queMin.push(num);
if (queMax.size() + 1 < queMin.size()) {
queMax.push(queMin.top());
queMin.pop();
}
}
else {
queMax.push(num);
if (queMax.size() > queMin.size()) {
queMin.push(queMax.top());
queMax.pop();
}
}
}
double findMedian() {
if (queMin.size() > queMax.size()) {
return queMin.top();
}
return (queMin.top() + queMax.top()) / 2.0;
}
};总结
看到这里 相信大家对这几道题的解题方法已经有了一定的理解了吧？如果你感觉这篇文章对你有帮助的话，希望你可以持续关注，订阅专栏，点赞收藏都是我创作的最大动力！
( 转载时请注明作者和出处。未经许可，请勿用于商业用途 )
更多文章请访问我的主页
