Educational Codeforces Round 127 (Rated for Div. 2)C~E
Educational Codeforces Round 127 (Rated for Div. 2)
Educational Codeforces Round 127 (Rated for Div. 2)
C. Dolce Vita
-
题意
给定长度为n的序列和一个消耗值m。
每一天序列中每一个元素都会增加1,每一天都可以用m去取序列中的一些数字,并且这些数字之和不超过m,并使得数字个数尽可能大,最终将数字个数进行一个累计。输出答案
思路1:
-
排序
核心模拟,二分时间点+暴力
二分找到时间点,同时暴力缩减区间更新至恰好不大于m。
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 1000000007
using namespace std;
const int N = 3E5 + 5, M = 6E5 + 10;
ll a[N], sum[N];
int main() {
int t;
cin >> t;
while (t--) {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> a[i];
sort(a + 1, a + n + 1);
int t = 0;
ll posr = 0;
ll res = 0;
ll curl = 0;
for (int i = 1; i <= n; i++) {
sum[i] = sum[i - 1] + a[i];
if (sum[i] <= m) {
posr = i;
}
}
res = posr;
int las = 0;
while (posr >= 1) {
ll l = curl, r = 1e9, ans = 0;
while (l <= r) {
ll mid = (l + r) >> 1;
if (sum[posr] + mid * posr <= m) {
l = mid + 1;
ans = mid;
} else
r = mid - 1;
}
res += (ans - las) * posr;
las = ans;
curl = ans + 1;
for (int i = posr; i >= 0; i--) {
if (sum[i] + i * curl <= m) {
posr = i;
break;
}
}
}
cout << res << endl;
}
return 0;
}
思路1优化
- 第一步缩减为可行的区间
- 第二步利用除法快速算出答案,因为在某个时间点下,某个前缀和对答案的贡献为总可使用的资源减去这个时间点下的前缀和后的差值除去个数。
思路2
- 排序,从前往后求取每一个前缀对答案的贡献(tourist)
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 1000000007
#define PB push_back
using namespace std;
const int N = 3E5 + 5, M = 6E5 + 10;
ll a[N], sum[N];
int main() {
int t;
cin >> t;
while (t--) {
ll n, m, res = 0, s = 0;
cin >> n >> m;
vector<ll> a(n + 1);
for (int i = 1; i <= n; i++)
cin >> a[i];
sort(a.begin() + 1, a.end());
for (int i = 1; i <= n; i++) {
s += a[i];
if (m >= s)
res += (m - s) / i + 1;
}
cout << res << endl;
}
return 0;
}
D. Insert a Progression
-
题意
-
给定长度为n的序列a和一个数字k,将1到k这k个数字插入到序列a中,求怎么插入使得从第二项开始,每一项和前一项差值的绝对值的累和最小。
思路
- 找到区间的最小值minn和最大值maxnn,就可以很方便将k个数字中minn到maxnn这些数字安放到minn和maxnn这段区间里面。
- 然后剩余的1到minn-1的数字就看情况进行插入(可以等效成只插入1这个数字,同理,也可以看成是只插入)可以插入到中间或者两边
- 如果是从中间进行插入,所带来的增值为2*abs(a[i]-1)
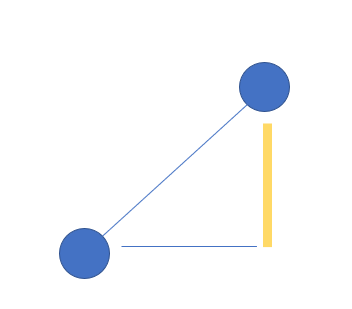
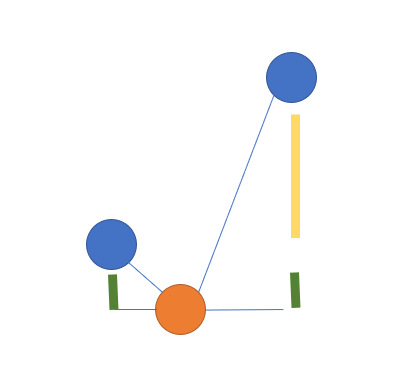
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 1000000007
#define PB push_back
using namespace std;
const int N = 3E5 + 5, M = 6E5 + 10;
ll a[N], sum[N];
int main() {
int t;
cin >> t;
while (t--) {
ll n, m, ans = 0, s = 0;
cin >> n >> m;
vector<ll> a(n + 1);
for (int i = 1; i <= n; i++)
cin >> a[i];
for (int i = 2; i <= n; i++)
ans += abs(a[i] - a[i - 1]);
ll add = 1e9;
ll maxn = *max_element(a.begin() + 1, a.end());
ll minn = *min_element(a.begin() + 1, a.end());
add = min({a[1] - 1, a[n] - 1, 2 * (minn - 1)});
ans += add;
if (maxn < m) {
add = 1e9;
add = min({m - a[1], m - a[n], 2 * (m - maxn)});
ans += add;
}
cout << ans << endl;
}
return 0;
}
E. Preorder
- 题意给定一棵完美二叉树,可以将任意结点的左右子树进行对调,求对调后的可以组成的不同的二叉树的数目。
- 将每一个子树的前序遍历先转成最小字典序(相当于挖掘出本质,如果左右子树的本质一样,则进行对调的话并不会产生贡献)。
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 998244353
#define PB push_back
using namespace std;
const int N = 3E5 + 5, M = 6E5 + 10;
ll a[N], sum[N];
int main() {
int n;
string s;
cin >> n;
cin >> s;
vector<string> pre_modi((1 << 18 ) + 1);
for (int i = 1; i <= ((1 << n) - 1); i++)
pre_modi[i] = string(1, s[i - 1]);
for (int i = (1 << (n - 1)) - 1; i >= 1; i--)
pre_modi[i] = pre_modi[i] + min(pre_modi[i << 1] + pre_modi[i << 1 | 1],
pre_modi[i << 1 | 1] + pre_modi[i << 1]);
ll ans = 1;
for (int i = 1; i <= (1 << (n - 1)) - 1; i++) {
if (pre_modi[i << 1] != pre_modi[i << 1 | 1]) {
ans <<= 1;
ans %= MOD;
}
}
cout << ans;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号