【数论】数论分块
【数论】数论分块
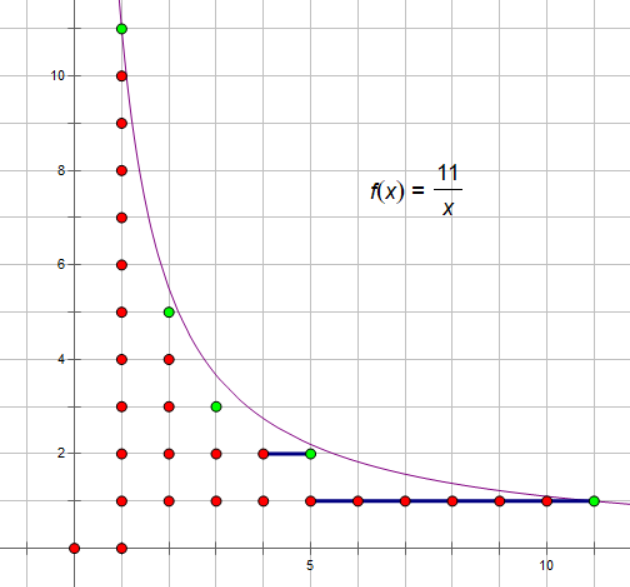
求解图中红点和绿点的总数之和。
求$$\sum_{i=1}^{n}k \space mod\space i$$?
如果纵轴的x一个点一个点进行移动的话,将会非常缓慢。
前置知识
\(k\%i=k-[\frac{k}i]\times i\)
于是有\(\sum_{i=1}^{n}k \space mod\space i=\sum_{i=1}^{n}k-[\frac{k}i]\times i=n\times k-\sum_{i=1}^{n}i\times[\frac{k}{i}]\)
所以我们重点是要去求取\(\sum_{i=1}^{n}i\times[\frac{k}{i}]\)的值。
若在一段区间内\([\frac{k}{i}]\)保持不变,可以将其看作是一个常数,而i是线性变化的,于是我们就可以通过等差数列的求和公式求出这一段区间的值。
而数论的分块(暂时的理解)是快速通过这些区间的左端点来求出区间的右端点,从而降低时间损耗。
就如图上的红点变成绿点,而不需要把每一个点都计算出答案。
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| \([\frac{11}{x}]\) | 11 | 5 | 3 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 |
对于任意一个i,求一个最大的j使得\([\frac{n}{i}]=[\frac{n}{j}]\)
且此时\(j=[\frac{n}{[\frac{n}{i}]}]\)
证明
令\(k=[\frac{n}{i}]<=\frac{n}{i}\) 。(k为商,即矩形所对应的高度)
-
则有\(j=[\frac{n}{k}]>=[\frac{n}{\frac{n}{i}}]=[i]=i\),所以j>=i(证明j在这个值下大于任意一个i)
-
前提引入,\([\frac{n}{i}]=[\frac{n}{j}]\)
进而在替换后有,\([\frac{n}{j}]=k\),所以有\(k<=\frac{n}{j}<k+1\),进一步有\(\frac{n}{k+1}<j<=\frac{n}{k}\)
j为整数,进而有\([\frac{n}{k}]=j_{max}\)
复杂度证明
通过打表不难发现,\(\lfloor\frac ni\rfloor\)最多有$2\cdot\sqrt n \(种取值,所以,整除分块的复杂度为\)O(\sqrt n)$。
证明:
若\(i\le\sqrt n\),显然最多有\(\sqrt n\)种取值(i的取值都只有\(\sqrt n\)种)。
若\(i>\sqrt n\),则\(\lfloor\frac ni\rfloor<\sqrt n\),取值亦不超过\(\sqrt n\)种。
模板题
P2261 [CQOI2007]余数求和

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 1000000007
using namespace std;
const int N = 3E5+5,M = 6E5+10;
ll n,k;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n>>k;
ll ans = n * k;
for(ll l=1,r;l<=n;l=r+1)
{
if(k/l!=0) r = min(k/(k/l),n);
else r = n;
ans -= (r-l+1)*(l+r)*(k/l)/2;
}
cout<<ans;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号