【数据结构】【莫队】回滚/不删除莫队
回滚/不删除莫队
概念
- 基础莫队(个人理解):将查询离线,对查询进行排序以达到更优的查询顺序,从而降低时间损耗。
- 应用:实现对一段区间某个个元素个数的查询。
- 基础莫队存在直接对区间左端点和右端点进行扩展或者删除的操作
问题引入

要求的是关乎区间的值(比如相同元素的最大相隔长度),因为无法确保删除左端点或者右端点是否会对这个关乎区间的值造成影响,所以干脆取消删除操作。
又由于莫队排序的方法,对于处在相同块的l所对应的r是单增的,所以这就可以很无脑的扩展就行了,但l相对来说就比较随机了,这个时候就暴力从l所在块的右端点扩展到l所在的位置就行了。
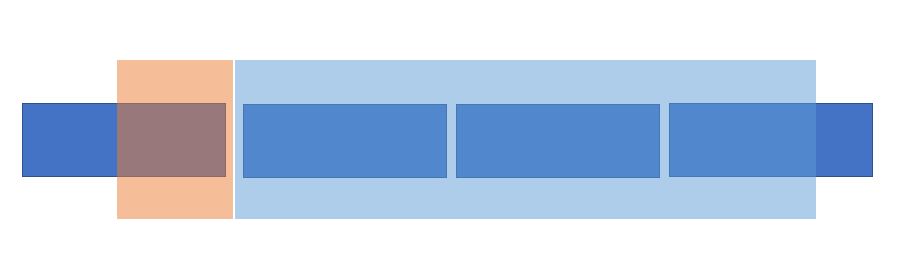
- (且由于r是单调递增的,所以这部分答案是可以反复利用,应该开一个变量去记忆蓝色部分的答案,方便下一个l同一个块的查询的使用)
- 且l会回滚回起点
当然,如果l和r处在同一个块中,就暴力计算就行了,最坏时间损耗为遍历整个块(单块块长)。
代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1E5+500;
int n,m,A[N],B[N],Rank[N];
ll ans[N];
struct Query{
int ql,qr,idx;
}qry[N];
void discrete()
{
sort(B+1,B+n+1);
int tot = unique(B+1,B+n+1)-B;
for(int i=1;i<=n;i++) Rank[i] = lower_bound(B+1,B+n+1,A[i]) - B;
}
int bel[N],bst[N],bed[N],blen,btot;
void build_block()
{
btot = blen = sqrt(n);
for(int i=1;i<=btot;i++)
{
bst[i] = blen*(i-1)+1;
bed[i] = blen*i;
}
if(bed[btot]<n)
btot++, bst[btot] = bed[btot-1]+1, bed[btot] = n;
for(int i=1;i<=btot;i++)
for(int j=bst[i];j<=bed[i];j++)
bel[j] = i;
}
bool cmp(Query& qa,Query& qb)
{
if(bel[qa.ql]==bel[qb.ql]) return qa.qr<qb.qr;
return qa.ql<qb.ql;
}
int bcnt[N];
ll brute(int ql,int qr)
{
ll res = 0;
for(int i=ql;i<=qr;i++) bcnt[ Rank[i] ] = 0;
for(int i=ql;i<=qr;i++)
{
bcnt[ Rank[i] ]++;
res = max(res,1ll*bcnt[ Rank[i] ]*A[i]);
}
return res;
}
int cnt[N];
void work()
{
int i = 1;
for(int blo=1;blo<=btot;blo++)
{
int l = bed[blo]+1, r = bed[blo];
ll res = 0;memset(cnt,0,sizeof(cnt));
for(;bel[ qry[i].ql ]==blo;i++)
{
int ql = qry[i].ql,qr = qry[i].qr;
if(bel[ql]==bel[qr])
ans[ qry[i].idx ] = brute(ql,qr);
else
{
ll temp = 0;
while(r<qr)
{
r++;
cnt[ Rank[r] ]++;
res = max(res,1ll*cnt[ Rank[r] ]*A[r] );
}
temp = res;
while(l>ql)
{
l--;
cnt[ Rank[l] ]++;
res = max(res,1ll*cnt[ Rank[l] ]*A[l] );
}
ans[ qry[i].idx ] = res;
//复原
while(l<bed[blo]+1)
{
cnt[ Rank[l] ]--;
l++;
}
//留给下一个查询进行使用
res = temp;
}
}
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
build_block();
for(int i=1;i<=n;i++)
cin>>A[i],B[i]=A[i];
discrete();
for(int i=1;i<=m;i++)
cin>>qry[i].ql>>qry[i].qr,qry[i].idx = i;
sort(qry+1,qry+m+1,cmp);
work();
for(int i=1;i<=m;i++) cout<<ans[i]<<endl;
return 0;
}
例题

#include<bits/stdc++.h>
#define ll long long
#define de(x) cout<<x<<endl;
using namespace std;
int const N = 2e5+500;
int A[N],B[N],Rank[N];
int n,m;
struct Query{
int ql,qr,idx;
}qry[N];
int blen;
int inline get(int x)
{
return (x-1)/blen;
}
bool cmp(Query& qa,Query& qb)
{
int bloa = get(qa.ql), blob = get(qb.ql);
if(bloa==blob) return qa.qr<qb.qr;
return qa.ql<qb.ql;
}
int bst[N],bed[N],bel[N],btot;
void build_block()
{
btot = blen = sqrt(n);
for(int i=1;i<=btot;i++)
{
bst[i] = (i-1)*blen+1;
bed[i] = i*blen;
}
if(bed[btot]<n)
btot++, bst[btot] = bed[btot-1] + 1, bed[btot] = n;
for(int i=1;i<=btot;i++)
for(int j=bst[i];j<=bed[i];j++)
bel[j] = i;
}
int fst[N];
vector<int> used;
int brute(int ql,int qr)
{
int res = 0;used.clear();
for(int i = ql;i<=qr;i++)
{
int val = Rank[i];
if(!fst[val]) fst[val] = i;
used.push_back(val); //bed[val] = i; //max(bed[val],i);
res = max(res,i-fst[val]);
}
for(int i=0;i<used.size();i++)
fst[used[i]] = 0;
return res;
}
int ans[N],last[N],pre[N];
void work()
{
int i = 1;
for(int blo=1;blo<=btot;blo++)
{
int l = bed[blo]+1, r = bed[blo];
int res = 0;
memset(last,0,sizeof(last));
memset(pre,0,sizeof(pre));
for(;bel[ qry[i].ql ]==blo;i++)
{
int ql = qry[i].ql, qr = qry[i].qr;
if(bel[ql]==bel[qr])
ans[ qry[i].idx ] = brute(ql,qr);
else
{
int temp = 0;
while(r<qr)
{
r++;
int val = Rank[r];
if(!pre[ val ]) pre[ val ] = r;
last[ val ] = r;
res = max(res,r - pre[val]);
}
temp = res;
while(l>ql)//往前面找就不必用到pre了
{
l--;
int val = Rank[l];
if(!last[ val ]) last[ val ] = l;
res = max(res,last[val] - l);
}
ans[ qry[i].idx ] = res;
l = bed[blo]+1;
res = temp;
}
}
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
build_block();
for(int i=1;i<=n;i++)
cin>>A[i],B[i] = A[i];
sort(B+1,B+n+1);
int tot = unique(B+1,B+n+1) - B;
for(int i=1;i<=n;i++) Rank[i] = lower_bound(B+1,B+n+1,A[i]) - B;
cin>>m;
for(int i=1;i<=m;i++)
cin>>qry[i].ql>>qry[i].qr,qry[i].idx = i;
sort(qry+1,qry+m+1,cmp);
work();
for(int i=1;i<=m;i++) cout<<ans[i]<<endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号