【String】字典树
字典树
字典树(Trie)是一个用来处理字符串的数据结构
字典树的建树的大概流程
新建一个没有内容(不储存任何字符)的结点,用来做起点
把每一个字符串的每一个位置看成是单独的一层,如果在某一个位置上有没有这个字母,如果没有的话,就在这一层新建一个能够代表这个字母意义的结点;如果有的话,就将上一层的结点连上这一层的这个结点。
字典树的代码实现
首先,在字典树的代码实现中,我们会使用一个next数组。
比如next[i][j](其中0<=j<=25,从小到大依次代表,a,b,c,d,e,f,...,z),代表的是第i个结点的下一个结点为字母j的结点标号。
其中next[i][j]==0代表以第i个结点的下一个储存内容为j的结点并没有存在。
因而我们需要对整个next数组做一个初始化
void init()
{
memset(next.0,sizeof(next));
}
(有点类似链式前向星)
处理一个字符串的函数
void insert(const string &s)
{
int cur = 1;//代表的是没有意义的那一个头结点
for(int i=0;i<s.length();i++)
{
if(!next[cur][s[i]-'a'])
next[cur][c-'a']=++cnt; //如果没有就临时创建一个结点,并赋予这个结点一个编号
cur = next[cur][c-'a']; //游标跑到下一个结点
}
//ed[cur]++;
}
查询某个前缀是否存在(看一下这个字符串能否在当前的字典树跑得完?)
同时cur最终停止的位置代表的是一个字符串末尾字符的位置,由于字典树造树的特性,我们可以知道最终的cur即代表着一个字符串。可以开一个数组ed去记录某种字符串的数量。
从不存储任何字母信息的结点(cur=1)开始,如果当前的结点连接到的下一个结点并没有存在的话,那么就直接返回false,否则就继续向下搜索,直到搜索完毕并且在搜索的过程中并没有产生任何的问题,那就返回true。
bool find_prefix(const string &s)
{
int cur = 1; //修正到起点
for(int i=0;i<=s.length();i++)
{
if(!next[cur][ s[i]-'a' ])
return false;
cur = next[cur][c-'a'];
}
return true;
}
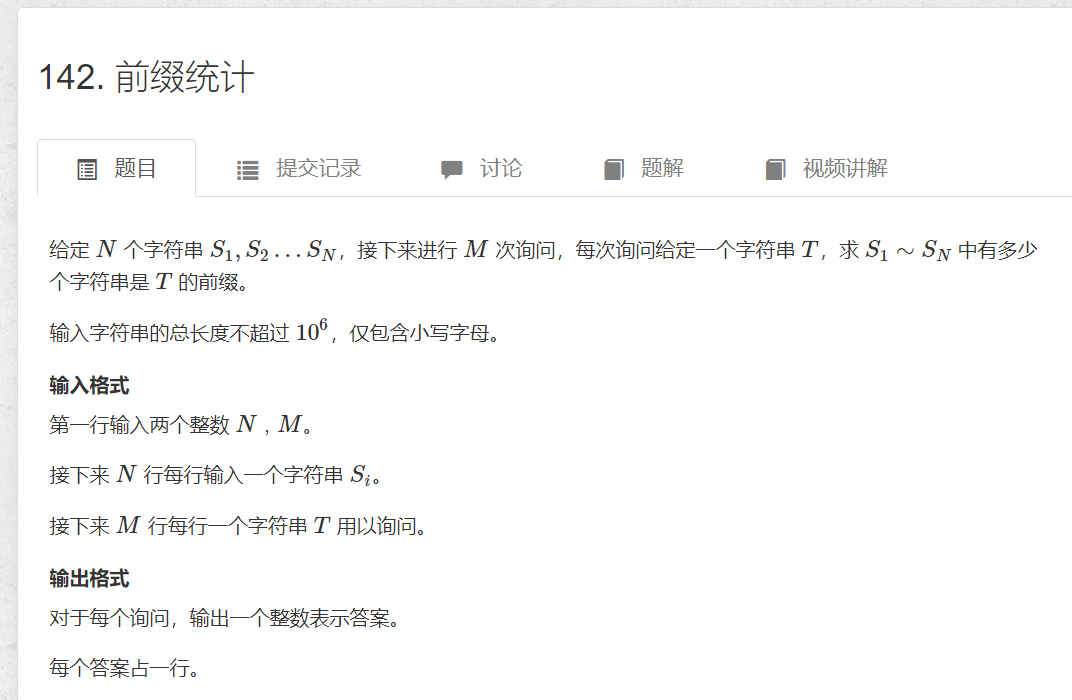
例题
#include <bits/stdc++.h>
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
using namespace std;
const int N = 1E5+10;
int n,m,cnt,ed[N],tr[N][26];
vector<string > vecs;
void init()
{
memset(tr,0,sizeof(tr));
cnt=2;
}
void build(const string &s)
{
int cur=1;
for(int i=0;i<s.length();i++)
{
if(!tr[cur][ s[i]-'a' ])
tr[cur][ s[i]-'a' ]=cnt++;
cur=tr[cur][ s[i]-'a' ];
}
ed[cur]++;
}
int find_prefix(const string &s)
{
int cur=1,res=0;
for(int i=0;i<s.length();i++)
{
cur=tr[cur][ s[i]-'a' ];
res += ed[cur];
}
return res;
}
int main()
{
init();
cin>>n>>m;
string s;
for(int i=1;i<=n;i++)
{
cin>>s;
build(s);
}
int res;
for(int i=1;i<=m;i++)
{
cin>>s;
cout<<find_prefix(s)<<endl;
}
return 0;
}


