【数据结构】分块入门1到9(Finished)
分块
分块的意思


分块就是将一段长区间(寿司条)分成一段段规格尽量统一的寿司,但技艺不精的新人厨师有的时候会不小心再两端的一端切出不符合规格标准(没有提前算好平均下去的规格,只是按既定的规格)的区间(从寿司的角度来理解,可以看成是边角料,从区间的角度,就是需要进行特殊处理的区间)。
把一个长度为\(n\)的区间分成几块看操作者的个人意愿,但这里建议分成\(\sqrt{n}\)块,为啥呢?
假设将长度为n的区间分成m块,每块长度就会为\([\frac{n}{m}]\),一般的话块与块之间的大小是相等的,同时也会把整个块当成一整份一起处理,但也有时会剩下一块或两块长度不一样(比较尴尬)的区间(看成是边角料吧,暂且称为零散块),而这块比较尴尬的块的区间长度是小于\([\frac{n}{m}]\) ,因而一次想要对长度为n的区间整个区间处理掉的话,就需要\(O(m+\frac{n}{m})\)(m是整块进行处理的块数,\(\frac{n}{m}\)是对零散块内所有的元素的个数,这里在最终形成\(m+\frac{n}{m}\)的时候应该是做了一些近似),根据均值不等式可知在\(m=\sqrt{n}\)的时候时间复杂度大O可以取到最小值,即\(O(\sqrt{n})\)(也称这种算法叫做根号算法),这种取法也意味着将长度为\(n\)的区间最终分成了长度为\(\sqrt{n}\)的\(\sqrt{n}\)块的区间,
如何写分块
首先,我们要定下标准,确定每一块块的规格,设规格变量为t。
inr t = sqrt(n);
然后每一块本质是一个区间,一个区间的的话,他就有区间本身的一些特性,比如说区间的左端点和右端点,用st数组来记录每一个区间的左端点,和用ed数组用来记录每一个区间的右端点,比如st[i],ed[i]表示的是第i个区间的左端点和右端点。
for(int i = 1;i <= t;i++)
{
st[i] = (i-1)*t+1;
ed[i] = i*t;
}
处理最后一块的两种写法
蓝书(开辟新的块)
t++;st[t]=ed[t-1]+1;ed[t]=n;
Pecco(拉长最后一块至包含到结尾)
注意,我们在分的过程中最后一块可能不是符合规格的块,我们要将最后一块所代表的区间的假设的右端点重新修改为真实的端点值。(拉长到实际长度)(为什么是拉长?是因为int t = sqrt(n);t相当于是根号n截尾后的数字,截尾截尾,截取一部分,相当于数字减少,所以\(t\times t<=n\))
ed[t] = n;
反过来,我们还需要对区间内的每一个元素打上标记,表明这个元素是属于哪一个块,取belong(归属)的前三个字母bel作为数据的名字,同时之前我们已经记好了每一个的块的左端点和右端点的位置,所以当我们要找到一个块里面的所有元素的位置的时候,我们只需要从左端点扫到右端点就行。
for(int i = 1;i <= t;i++)
for(int j = st[i]; j <= ed[i]; j++)
bel[j] = i;
- 代码注释,j代表的是第i块里面的元素,即元素j是属于第i块的。
同时,通过左端点位置和右端点位置的差值的绝对值,我们可以也可以得到每一个块的区间长度:(比较鸡肋)(注意,如果使用万能库的话,会发生冲突)
for(int i = 1; i <= t;i++)
size[i] = ed[i] - st[i] + 1;
除此之外,我们还可以用一个sum数组用来统计区间和
for(int i = 1; i <= n; i++)
cin>>A[i];
for(int i = 1; i <= t; i++)
for(int j = st[i]; j <= ed[i]; j++)
sum[i] += A[j];
分块的用途
实现对区间l到r的加减,并最终能够查询到区间内某一个点的值。
区间修改(加减部分)
- 增量标记add,有点类似线段树的懒标记,如果对整个块进行加减的话,就可以使用增量标记来说明整个块加了多少(最终再进行结算),那如果是处理到零散块,就暴力解决或者
sum[i] = (et[i]-l+1) * d(sum[i] = (r-st[i]+1)*d)
l和r在同一块
if( bel[l] == bel[r])
{
for(int i = l; i <= r ; i++)
{
A[i]++;
sum[ bel[i] ]+=k;
}
}
l和r不在同一块
- 零散块暴力处理,整块整块处理
if( bel[l] != bel[r] ){ for(int i = l; i <= ed[ bel[l] ] ; i++) { A[i]++; sum[ bel[i] ] += k; } for(int i = bel[l] + 1 ; i <= bel[r] - 1 ; i++) add[i] += k; for(int i = st[ bel[r] ] - 1 ; i <= r ; i++) { A[i]++; sum[ bel[i] ] += k; }}
LOJ#6277. 数列分块入门 1
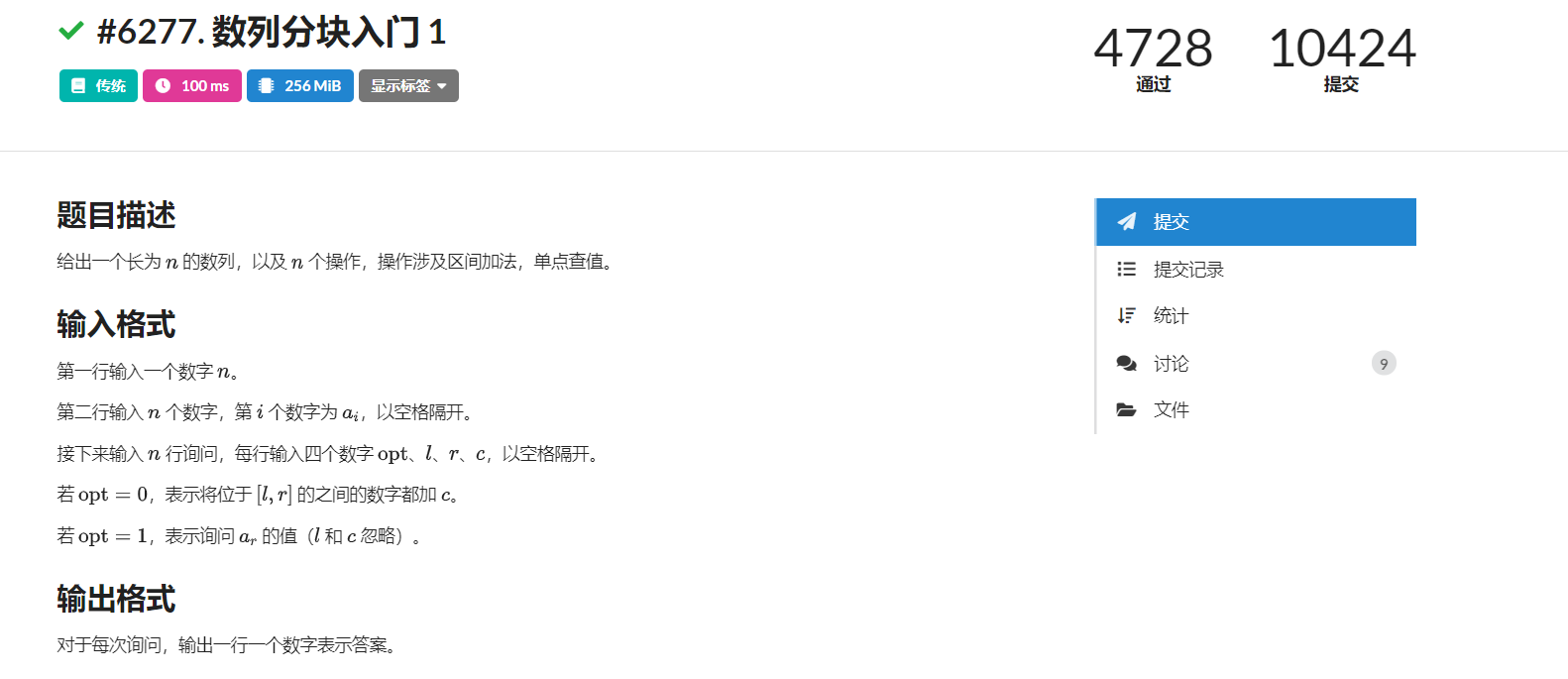
#include <bits/stdc++.h>#define ll long long#define rep(i,x,n) for(int i=x;i<n;i++)#define repd(i,x,n) for(int i=x;i<=n;i++)using namespace std;const int N = 5e4+10;int st[N],ed[N],add[N],A[N],bel[N];int n,m,t;void modi(int l,int r,int k) { if(bel[l]==bel[r]) repd(i,l,r) A[i]+=k; else { repd(i,l,ed[ bel[l] ]) A[i]+=k; repd(i,bel[l]+1,bel[r]-1) add[i]+=k; repd(i,st[ bel[r] ],r) A[i]+=k; }}int main() { memset(add,0,sizeof(add)); scanf("%d",&n); t=sqrt(n); repd(i,1,t) { st[i]=(i-1)*t+1; ed[i]=i*t; } if(ed[t]<n) t++,st[t]=ed[t-1]+1,ed[t]=n; repd(i,1,t) repd(j,st[i],ed[i]) bel[j]=i; repd(i,1,n) scanf("%d",&A[i]); int opt,l,r,c; int k=n; while(k--) { scanf("%d%d%d%d",&opt,&l,&r,&c); if(opt==1) printf("%d\n",add[ bel[r] ]+A[r]); else modi(l,r,c); } return 0;}
实现对区间l到r的加减,并最终能够读取任意的区间和
AcWing 243. 一个简单的整数问题2
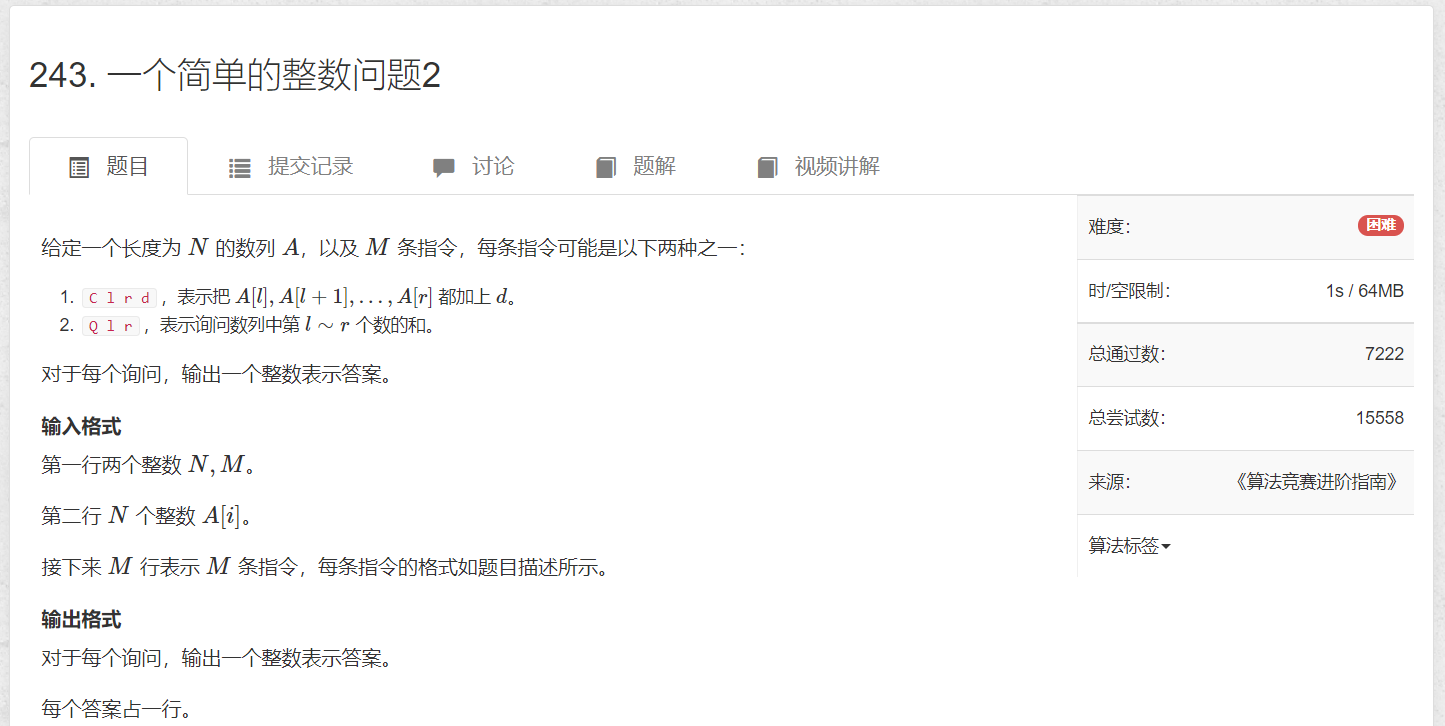
#include <bits/stdc++.h>#define ll long long#define repd(i,x,n) for(int i=x;i<=n;i++)#define de() cout<<"res = "<<res<<endl;using namespace std;const int NN = 320, N = 1E5+10;int st[NN],ed[NN],add[NN],t,A[N],bel[N];ll sum[N];ll ask(int l,int r){ ll res=0; if(bel[l]==bel[r]) { res = add[ bel[l] ] * (r-l+1); repd(i,l,r) res+= A[i]; return res; } //整块的处理 repd(i,bel[l]+1,bel[r]-1) res += add[i] * (ed[i] - st[i] + 1) + sum[i]; //零散块 repd(i,l,ed[ bel[l] ]) res += A[i] + add[ bel[i] ]; repd(i,st[ bel[r] ],r) res += A[i] + add[ bel[i] ]; return res;}void modi(int l,int r,int k){ if(bel[l]==bel[r]) { repd(i,l,r) A[i] += k; sum[ bel[l] ] += (r-l+1) * k; } else { repd(i,l,ed[ bel[l] ]) { A[i] += k; sum[ bel[i] ] += k; } repd(i,bel[l]+1,bel[r]-1) add[i] += k; repd(i,st[ bel[r] ],r) { A[i] += k; sum[ bel[i] ] += k; } }}int main(){ memset(sum,0,sizeof(sum)); memset(add,0,sizeof(add)); int n,q; cin>>n>>q; int t = sqrt(n); repd(i,1,t) { st[i] = (i-1)*t+1; ed[i] = i*t; } if(ed[t]<n) t++,st[t] = ed[t-1] + 1,ed[t] = n; repd(i,1,t) repd(j,st[i],ed[i]) bel[j] = i; repd(i,1,n) { cin>>A[i]; sum[ bel[i] ] += A[i]; } int l,r,k; char op; while(q--) { cin>>op; cin>>l>>r; if(op=='Q') cout<<ask(l,r)<<endl; else { cin>>k; modi(l,r,k); } } return 0;}
实现对区间l到r的加减,并最终能够查询到区间内大于某个特定的值的个数(整块二分,零散块暴力)
先考虑一个简化版的问题,如果给你一个比较小的区间,让你直接查询这个区间内大于等于c的数字的个数,你该怎么做?
- 朴素的想法就是直接扫过去,满足条件的就记录的计数器里面去
- 第二种想法是先对这个区间排个序,找到第一个大于这个特定值的数字的位置,那么在这个位置后面的数字都将会满足条件(答案也就是位置差)。
- 第二种想法的实现可以借助二分的思想来优化时间复杂度(二分的前提是有序,所以要先进行排序,注意这种排序是块内部的排序,且排序完元素的位置会被打乱,而如果查询是针对元素原来的位置的话,那么,就需要保留原有的数组,并借助一个新的数组来存放原有数组实时更新后的结果,以便查询)。
而用分块来解决这类问题的话会同时结合以上两种做法(整块的话会采取第二种想法的做法,零散块的话会采取第一种朴素的想法的做法)。
LOJ #6278. 数列分块入门 2
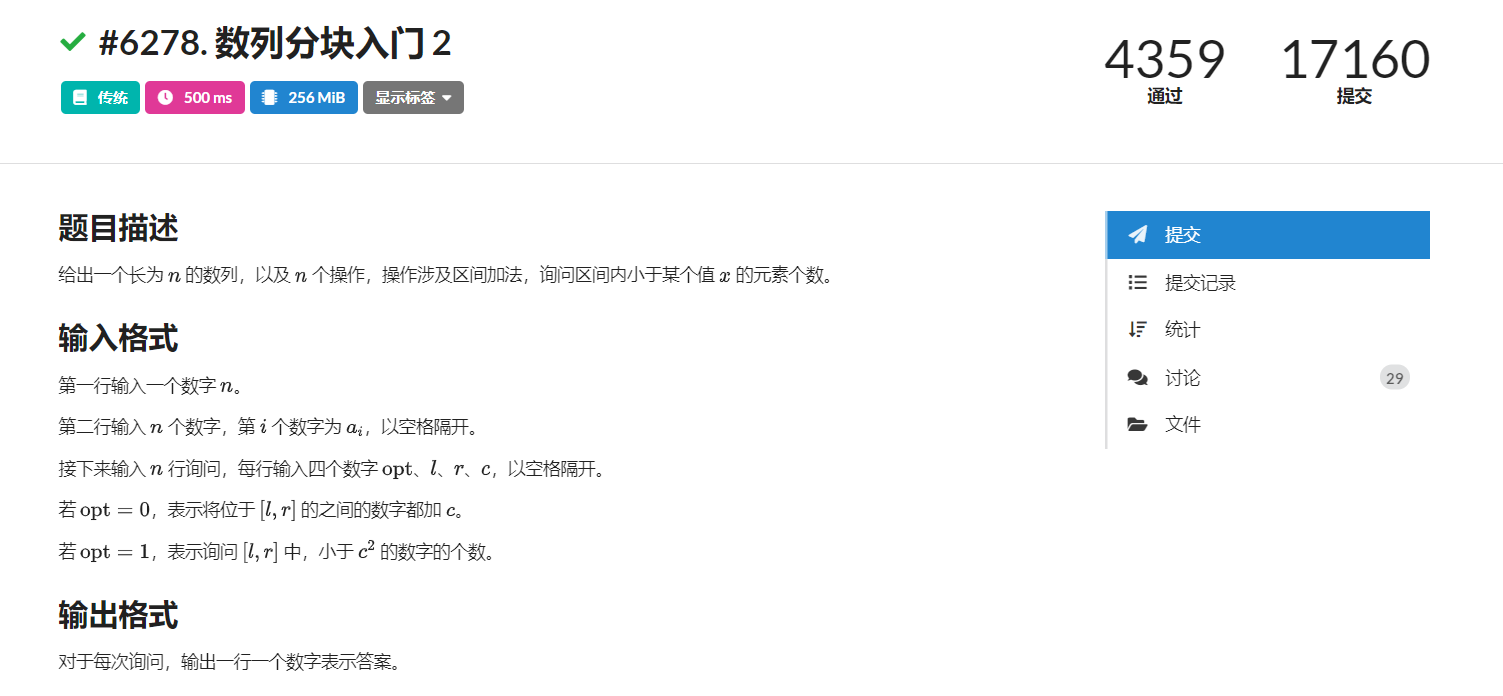
#include <bits/stdc++.h>#define ll long long#define repd(i,x,n) for(int i=x;i<=n;i++)using namespace std;const int N = 5E4+10;int n,t,st[N],ed[N],add[N],bel[N],A[N],B[N];void initB(int x){ repd(i,st[x],ed[x]) B[i] = A[i]; sort(B+st[x],B+ed[x]+1);}void modi(int l,int r,int c){ if(bel[l]==bel[r]) { repd(i,l,r) A[i]+=c; initB(bel[l]); } else { repd(i,l,ed[ bel[l] ]) A[i]+=c; initB(bel[l]); repd(i,bel[l]+1,bel[r]-1) add[i]+=c; repd(i,st[ bel[r] ],r) A[i]+=c; initB(bel[r]); }}int ask(int l,int r,int val){ int res=0; if(bel[l]==bel[r]) { repd(i,l,r) res+=( (A[i]+add[ bel[i] ])<val?1:0 ); } else { repd(i,l,ed[ bel[l] ]) res+=( (A[i]+add[ bel[i] ])<val?1:0); repd(i,bel[l]+1,bel[r]-1) res+=lower_bound(B+st[i],B+ed[i]+1,val)-(B+st[i])+1; repd(i,st[ bel[r] ],r ) res+=( (A[i]+add[ bel[i] ])<val?1:0); } return res; }int main(){ scanf("%d",&n); t = sqrt(n); repd(i,1,t) { st[i]=(i-1)*t+1; ed[i]=i*t; } if(ed[t]<n)t++,st[t]=ed[t-1]+1,ed[t]=n; repd(i,1,n) { scanf("%d",&A[i]); B[i] = A[i]; } repd(i,1,n) { int opt,l,r,c; scanf("%d%d%d%d",&opt,&l,&r,&c); if(opt==1) printf("%d\n",ask(l,r,c*c)); else modi(l,r,c); } return 0;}
实现对区间l到r的加减,并最终能够查询得到区间内小于某个值的前驱(整块二分,散块暴力)
向lower_bound函数传入一个数组和一个值,返回的是这个有序数组中第一个大于或等于这个数的数组元素所对应的位置。而如果返回的是整个数组的长度(一般再减去数组名,即数组的首地址),意味着,数组内所有的元素都小于这个值;那如果返回的是0的话,意味着,这个有序且递增的数组的首个元素的数值是大于或等于这个值,换句话说,也就是数组内所有的元素都是大于或等于这个值。
LOJ#6279. 数列分块入门 3
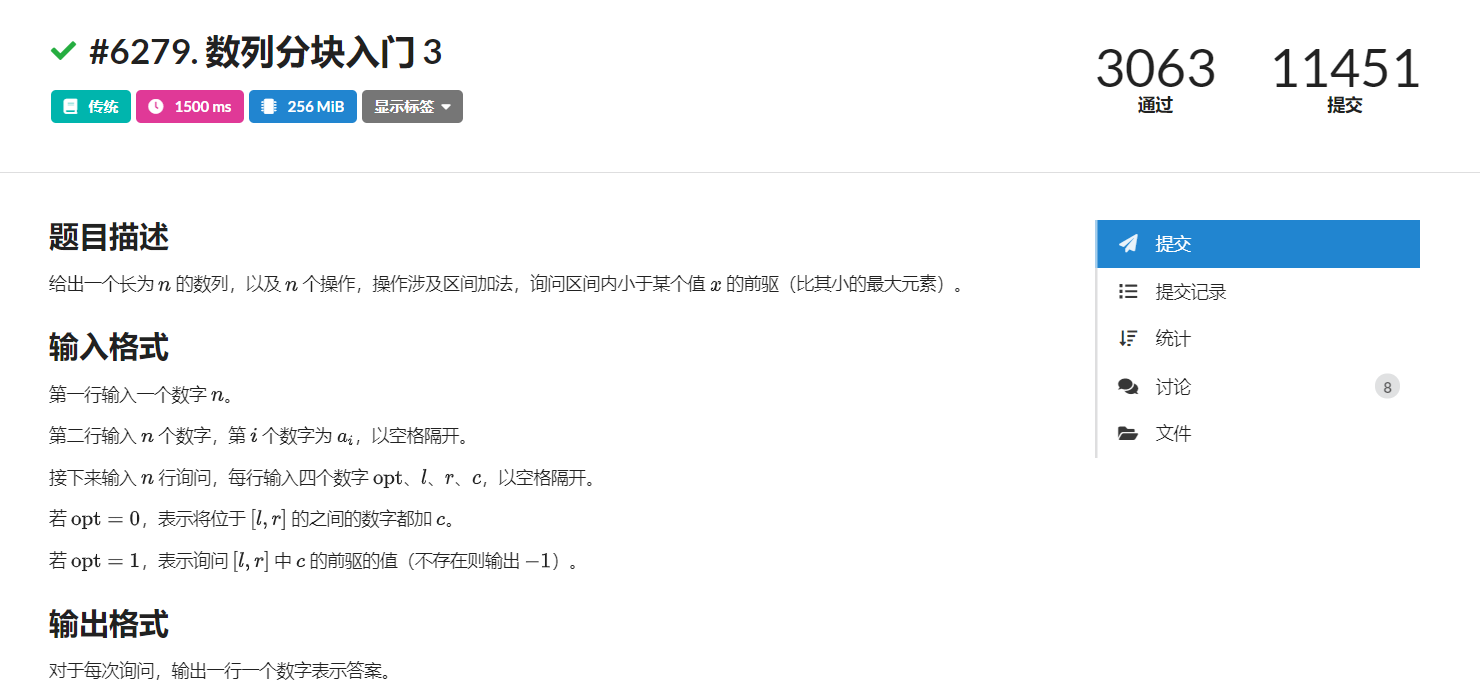
#include <bits/stdc++.h>#define MEM(a,x) memset(a,x,sizeof(a))#define W(a) while(a)#define gcd(a,b) __gcd(a,b)#define pi acos(-1.0)#define PII pair<int,int>#define pb push_back#define mp make_pair#define fi first#define se second#define ll long long#define ull unsigned long long#define rep(i,x,n) for(int i=x;i<n;i++)#define repd(i,x,n) for(int i=x;i<=n;i++)#define MAX 1000005#define MOD 1000000007#define INF 0x3f3f3f3f3f3f3f3f#define lowbit(x) (x&-x)using namespace std;const int N = 1e5+10,KN = 1E3;int n,t;int bel[N],add[KN],st[KN],ed[KN],A[N],B[N];int ask(int l,int r,int c){ int ans=-1; if(bel[l]==bel[r]) { repd(i,l,r) if( (A[i]+add[ bel[i] ]<c) && (A[i]+add[ bel[i] ]>ans) ) ans = A[i]+add[ bel[i] ]; } else { repd(i,l,ed[bel[l]]) if( (A[i]+add[ bel[i] ]<c)&&(A[i]+add[ bel[i] ]>ans) ) ans = A[i]+add[bel[i]]; repd(i,bel[l]+1,bel[r]-1) { if(B[st[i]]+add[i]>=c) continue; int pos=lower_bound(B+st[i],B+ed[i]+1,c-add[i])-B;//是在整个B的排行 int tpos=pos-1; if(B[tpos]+add[bel[tpos]]>ans) ans=B[tpos]+add[bel[tpos]]; } repd(i,st[bel[r]],r) if( (A[i]+add[ bel[i] ]<c)&&(A[i]+add[ bel[i] ]>ans) ) ans = A[i]+add[bel[i]]; } return ans;}void reset(int x){ repd(i,st[x],ed[x]) B[i]=A[i]; sort(B+st[x],B+ed[x]+1);}void modi(int l,int r,int k){ if(bel[l]==bel[r]) { repd(i,l,r) A[i]+=k; reset(bel[l]); } else { repd(i,l,ed[ bel[l] ]) A[i]+=k; reset(bel[l]); repd(i,bel[l]+1,bel[r]-1) add[i]+=k; repd(i,st[ bel[r] ],r) A[i]+=k; reset(bel[r]); }}int main(){ memset(add,0,sizeof(add)); cin>>n; t = sqrt(n); repd(i,1,t) { st[i] = (i-1)*t+1; ed[i] = i*t; } if(ed[t]<n) t++,st[t] = ed[t-1] + 1, ed[t] = n; repd(i,1,t) { repd(j,st[i],ed[i]) cin>>A[j],bel[j]=i; reset(i); } repd(i,1,n) { int opt,l,r,c; cin>>opt>>l>>r>>c; if(!opt) modi(l,r,c); else cout<<ask(l,r,c)<<endl; } return 0;}
实现对区间l到r的加减,并最终能够查询到区间和对某个数取余后的结果
LOJ#6279. 数列分块入门 4

#include <bits/stdc++.h>#define MEM(a,x) memset(a,x,sizeof(a))#define W(a) while(a)#define gcd(a,b) __gcd(a,b)#define pi acos(-1.0)#define PII pair<int,int>#define pb push_back#define mp make_pair#define fi first#define se second#define ll long long#define ull unsigned long long#define rep(i,x,n) for(int i=x;i<n;i++)#define repd(i,x,n) for(int i=x;i<=n;i++)#define MAX 1000005#define MOD 1000000007#define INF 0x3f3f3f3f#define lowbit(x) (x&-x)using namespace std;const int N = 5e4+10,KN = 1e3+10;ll n,t,st[KN],ed[KN],bel[N],A[N],add[KN],sum[KN];void modi(int l,int r,int c){ if(bel[l]==bel[r]) { repd(i,l,r) A[i]+=c,sum[ bel[i] ]+=c; } else { repd(i,l,ed[ bel[l] ]) A[i]+=c,sum[ bel[i] ]+=c; repd(i,st[ bel[r] ],r) A[i]+=c,sum[ bel[i] ]+=c; repd(i,bel[l]+1,bel[r]-1) add[i]+=c,sum[i]+=(ed[i]-st[i]+1)*c; }}ll ask(int l,int r,int c){ ll res=0; if(bel[l]==bel[r]) { repd(i,l,r) res+=A[i]+add[bel[i]],res%=(c+1); } else { repd(i,l,ed[ bel[l] ]) res+=A[i]+add[bel[i]],res%=(c+1); repd(i,st[ bel[r] ],r) res+=A[i]+add[bel[i]],res%=(c+1); repd(i,bel[l]+1,bel[r]-1) res+=sum[i],res%=(c+1); } return res%(c+1);}int main(){ memset(add,0,sizeof(add)); memset(sum,0,sizeof(sum)); cin>>n; int t = sqrt(n); repd(i,1,t) { st[i]=(i-1)*t+1; ed[i]=i*t; } if(ed[t]<n) t++,st[t]=ed[t-1]+1,ed[t]=n; repd(i,1,t) { repd(j,st[i],ed[i]) cin>>A[j],sum[i]+=A[j],bel[ j ] = i; //cout<<"debug: "<<st[i]<<" "<<ed[i]<<" "<<sum[i]<<endl; } repd(i,1,n) { int opt,l,r,c; cin>>opt>>l>>r>>c; if(!opt) modi(l,r,c); else cout<<ask(l,r,c)<<endl; } return 0;}
在l到r的区间内添加一个数字,并能够去查询到区间内某个位置上的值(vector版分块)
借助STL中的vector来实现
- 一个vector代表一个块
vector获取块的长度
vec[i].size();
在vector的某个位置插入某元素x
vec[i].insert(vec[i].begin()+偏移量-1,x);
用vector对所有块进行重新分块
void rebuild(){ 重置临时的普通数组 将每一个vector块中的元素依照归属的vector的顺序及其内部顺序来暂时压入到这个普通的数组中去,并记得将vector清零(重新来过) 重新来过}
利用块来确定位置
这不单要查明是在第几个块和这个块里面的第几个位置。
可以写一个函数,并用一个pair对去接收这对信息
pair<int,int> find_pos(int r){ int cnt; for(int i=1;i<=t;i++) { if(r>vec[i].size()) r-=vec[i].size(); else cnt=i,break; } return make_pair(cnt,r);}void modi(int l,int x){ pair<int,int> pos=find_pos(l); vec[pos.first].insert(vec[pos.first].begin()+pos.second-1,r);//由于vector数组的下标是从零开始的所以需要找到位置后,要将这个位置再剪掉1。}
实现区间开方和区间和查询
LOJ#6279. 数列分块入门 5
#include <bits/stdc++.h>
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define pi acos(-1.0)
#define PII pair<int,int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 1000000007
#define INF 0x3f3f3f3f
#define lowbit(x) (x&-x)
using namespace std;
const int N = 5E4+10,KN =300;
int A[N],bel[N],sum[N],st[N],ed[N],flag[N];
int t,n;
inline void update(int x)
{
if(flag[x]) return;
flag[x]=1;
repd(i,st[x],ed[x])
{
sum[x]-=A[i];
A[i]=sqrt(A[i]);
sum[x]+=A[i];
if(A[i]>1) flag[x]=0;
}
}
inline ll ask(int l,int r)
{
ll ans=0;
if(bel[l]==bel[r])
repd(i,l,r) ans+=A[i];
else
{
repd(i,l,ed[ bel[l] ])
ans+=A[i];
repd(i,bel[l]+1,bel[r]-1)
ans+=sum[i];
repd(i,st[ bel[r] ],r)
ans+=A[i];
}
return ans;
}
inline void extract(int l,int r)
{
if(bel[l]==bel[r])
{
repd(i,l,r)
{
sum[ bel[i] ]-=A[i];
A[i]=sqrt(A[i]);
sum[ bel[i] ]+=A[i];
}
}
else
{
repd(i,l,ed[ bel[l] ])
{
sum[ bel[i] ]-=A[i];
A[i]=sqrt(A[i]);
sum[ bel[i] ]+=A[i];
}
repd(i,st[ bel[r] ],r)
{
sum[ bel[i] ]-=A[i];
A[i]=sqrt(A[i]);
sum[ bel[i] ]+=A[i];
}
repd(i,bel[l]+1,bel[r]-1)
update(i);
}
}
int main()
{
scanf("%d",&n);
t=sqrt(n);
repd(i,1,t)
{
st[i]=(i-1)*t+1;
ed[i]=i*t;
}
if(ed[t]<n)t++,st[t]=ed[t-1]+1,ed[t]=n;
repd(i,1,t)
repd(j,st[i],ed[i])
{
scanf("%d",&A[j]);
bel[j]=i;
sum[i]+=A[j];
}
repd(i,1,n)
{
int opt,l,r,c;
scanf("%d%d%d%d",&opt,&l,&r,&c);
if(opt) printf("%lld\n",ask(l,r));
else extract(l,r);
}
return 0;
}
LOJ6282. 数列分块入门 6
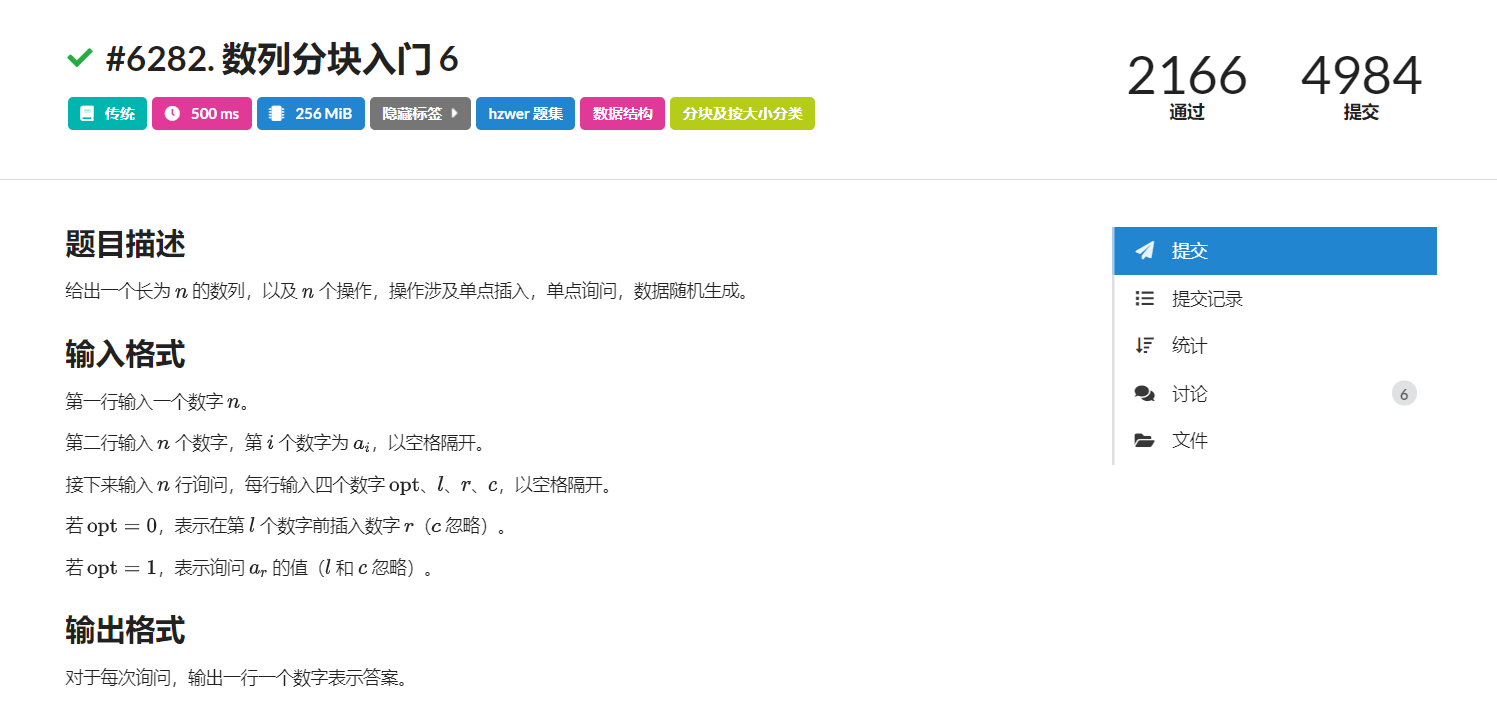
#include <bits/stdc++.h>#define MEM(a,x) memset(a,x,sizeof(a))#define W(a) while(a)#define gcd(a,b) __gcd(a,b)#define pi acos(-1.0)#define PII pair<int,int>#define pb push_back#define mp make_pair#define fi first#define se second#define ll long long#define ull unsigned long long#define rep(i,x,n) for(int i=x;i<n;i++)#define repd(i,x,n) for(int i=x;i<=n;i++)#define MAX 1000005#define MOD 1000000007#define INF 0x3f3f3f3f#define lowbit(x) (x&-x)using namespace std;const int N =1E5+10,KN = 1E5+10;int n,m,t,x,st[KN],ed[KN],A[N];vector<int> vec[KN];pair<int,int> find_pos(int r){ repd(i,1,t) { if(r>vec[i].size()) r-=vec[i].size(); else return make_pair(i,r); }}void reblock(){ int cur=0; repd(i,1,t) { rep(j,0,vec[i].size()) A[++cur]=vec[i][j]; vec[i].clear(); } t=sqrt(cur); repd(i,1,t) { st[i]=(i-1)*t+1; ed[i]=i*t; } if(ed[t]<cur) t++,st[t]=ed[t-1]+1,ed[t]=cur; repd(i,1,t) repd(j,st[i],ed[i]) vec[i].push_back(A[j]);}int ask(int r){ pair<int,int> info=find_pos(r); return vec[ info.fi ][ info.se-1 ];}void insert(int l,int x){ pair<int,int> info=find_pos(l); vec[ info.fi ].insert(vec[ info.fi ].begin() + info.se - 1,x); if( vec[ info.fi ].size()>3*t) reblock(); }int main(){ cin>>n; t=sqrt(n); repd(i,1,t) { st[i]=(i-1)*t+1; ed[i]=i*t; } if(ed[t]<n)t++,st[t]=ed[t-1]+1,ed[t]=n; repd(i,1,t) repd(j,st[i],ed[i]) { cin>>x; vec[i].push_back(x); } repd(i,1,n) { int opt,l,r,c; cin>>opt>>l>>r>>c; if(opt) cout<<ask(r)<<endl; else insert(l,r); } return 0;}
实现区间乘和区间加,并且最终能够查询到特定位置的数字
这类问题我们需要两种标记,一种标记去记录加法的量,另外一种标记去记录乘法的量,而这个标记是针对单独的整个的小块。且不同于以往的只是求区间和地分块问题的散块,不能再那么简简单单地去对加法标记做处理就行,而是在遇到乘法要求时,需要将所有的加法标记和减法标记所带来的效果实现到散块中的每一个元素,并将这两种标记给初始化。(注意:乘法标记是针对当前的区间的标记,最终结算的时候是对整个当下的区间,而如果在处理散块时,如果没有及时清理(转化掉这些标记),最终在结算的时候,乘法标记也将会放大这些没有关系的标记,造成误差)。
而且块的加法标记保留的是最新更新的数据(A[i]的数据是过时的),所以加法标记被乘法处理是没有问题的。
LOJ#6283. 数列分块入门 7
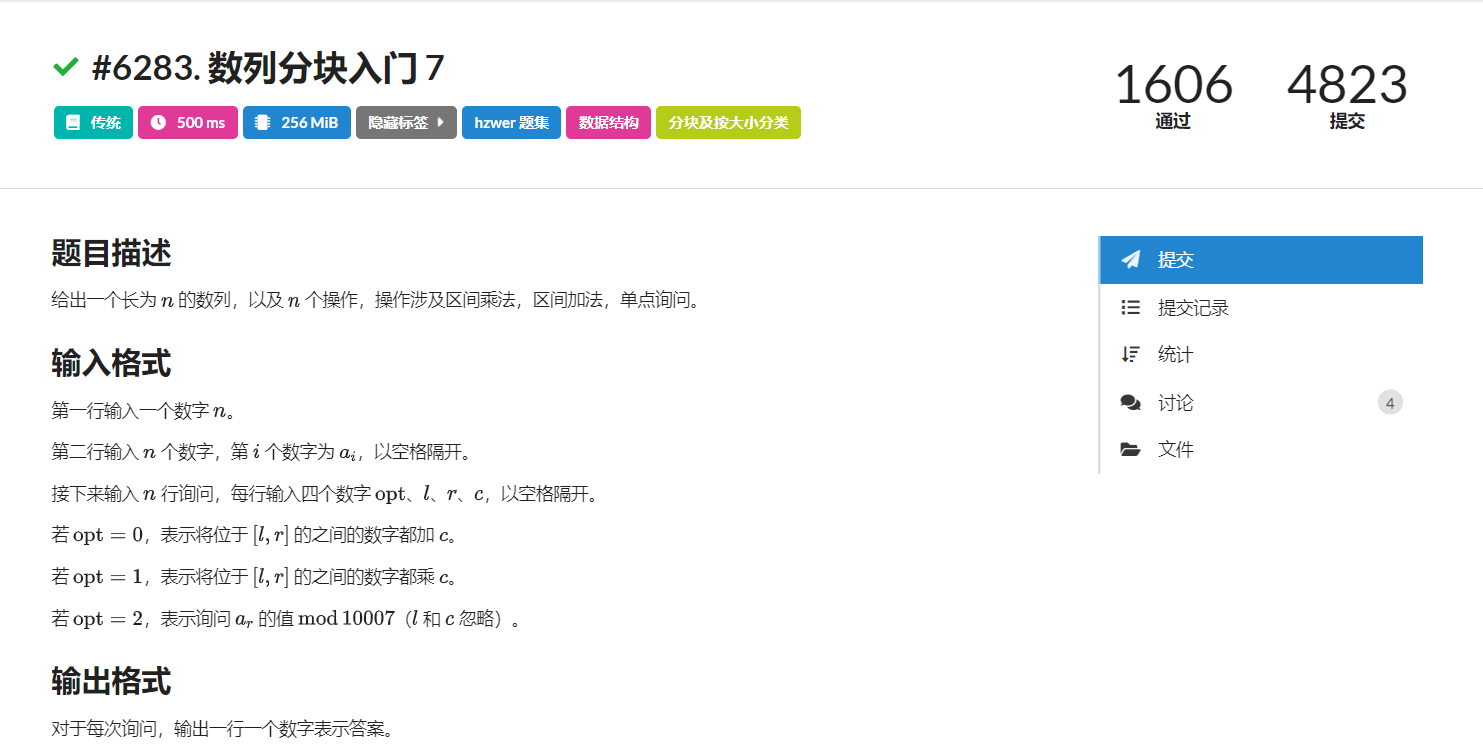
#include <bits/stdc++.h>
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define pi acos(-1.0)
#define PII pair<int,int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 10007
#define INF 0x3f3f3f3f
#define lowbit(x) (x&-x)
using namespace std;
const int N = 1E5+10, KN = 1E5+10;
int n,t,A[N],bel[N],add[KN],mul[KN],st[N],ed[N];
void one_reset(int x)
{
repd(i,st[x],ed[x])
A[i]=(A[i]*mul[x]+add[x])%MOD;
mul[x]=1,add[x]=0;
}
void modi(int opt,int l,int r,int c)
{
if(bel[l]==bel[r])
{
one_reset( bel[l] );
repd(i,l,r)
if(opt) A[i]=A[i]*c%MOD;
else A[i]=(A[i]+c)%MOD;
}
else
{
one_reset(bel[l]);
one_reset(bel[r]);
repd(i,l,ed[ bel[l] ])//由于零散块的标记已经被清零过了,所以不用考虑太多,直接进行操作就好
if(opt)
A[i]=A[i]*c%MOD;
else A[i]=(A[i]+c)%MOD;
repd(i,st[ bel[r] ],r)
if(opt)
A[i]=A[i]*c%MOD;
else A[i]=(A[i]+c)%MOD;
repd(i,bel[l]+1,bel[r]-1)
{
if(opt)
add[i]=(add[i]*c)%MOD,mul[i]=(mul[i]*c)%MOD;
else add[i]=(add[i]+c)%MOD;
}
}
}
int ask(int r)
{
return (A[r]*mul[ bel[r] ]+add[ bel[r] ])%MOD;
}
int main()
{
cin>>n;
t=sqrt(n);
repd(i,1,t)
{
st[i]=(i-1)*t+1;
ed[i]=i*t;
add[i]=0,mul[i]=1;
}
if(ed[t]<n)t++,st[t]=ed[t-1]+1,ed[t]=n,add[t]=0,mul[t]=1;
repd(i,1,t)
repd(j,st[i],ed[i])
cin>>A[j],bel[j]=i;
repd(i,1,n)
{
int opt,l,r,c;
cin>>opt>>l>>r>>c;
if(opt==2) cout<<ask(r)<<endl;
else modi(opt,l,r,c);
}
return 0;
}
实现区间整段某个值的覆盖
基本思路:给整块一个标记,这个标记用来说明这个块是否值都是相同的,如果是的话,遇到整块的修改,只需要改动这个标记就行,而不用整个块内的所有元素都改一遍。
LOJ#6285. 数列分块入门 8
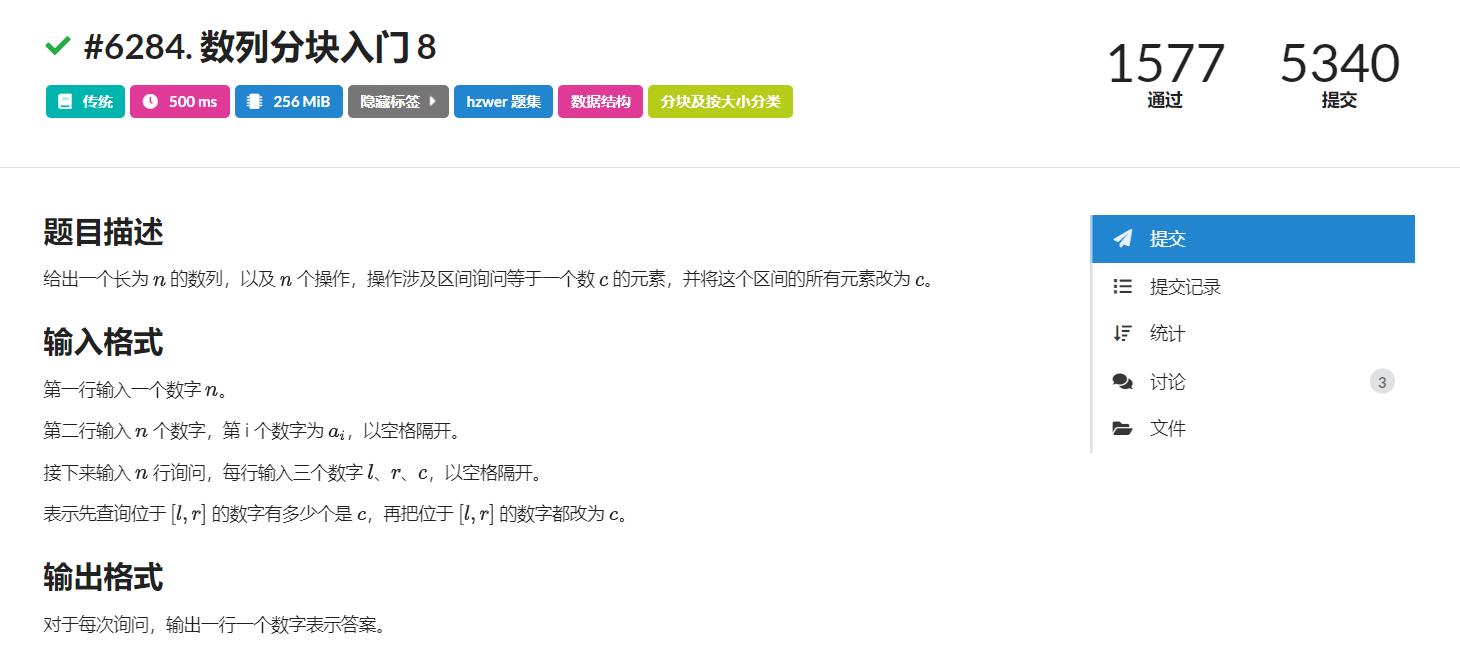
#include <bits/stdc++.h>
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define pi acos(-1.0)
#define PII pair<int,int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 1000000007
#define INF 0x3f3f3f3f
#define lowbit(x) (x&-x)
using namespace std;
const int N = 1E5+10,KN = 1E3+10;
int n,t,tag[N],st[N],ed[N],bel[N],A[N];
void update(int x)
{
if(tag[x]==-1)
return;
repd(i,st[x],ed[x])
A[i]=tag[x];
tag[x]=-1;
}
int work(int l,int r,int c)
{
int res=0;
if(bel[l]==bel[r])
{
update(bel[l]);
if(tag[bel[l]]==c) res+=r-l+1;
else
repd(i,l,r)
if(A[i]==c)
res++;
else A[i]=c;
}
else
{
update(bel[l]);
if(tag[bel[l]]==c) res+=ed[bel[l]]-l+1;
else repd(i,l,ed[ bel[l] ])
if(A[i]==c)
res++;
else A[i]=c;
update(bel[r]);
if(tag[bel[r]]==c) res+=r-st[bel[r]]+1;
else repd(i,st[bel[r]],r)
if(A[i]==c)
res++;
else A[i]=c;
repd(i,bel[l]+1,bel[r]-1)
{
if(tag[i]!=-1)
{
if(tag[i]==c)
res+=ed[i]-st[i]+1;
else tag[i]=c;
}
else
{
repd(j,st[i],ed[i])
{
if(A[j]==c)
res++;
else A[j]=c;
}
tag[i]=c;
}
}
}
return res;
}
int main()
{
memset(tag,-1,sizeof(tag));
cin>>n;
t = sqrt(n);
repd(i,1,t)
{
st[i]=(i-1)*t+1;
ed[i]=i*t;
}
if(ed[t]<n) t++,st[t]=ed[t-1]+1,ed[t]=n;
repd(i,1,t)
repd(j,st[i],ed[i])
scanf("%d",&A[j]),bel[j]=i;
int l,r,x;
repd(i,1,n)
{
scanf("%d%d%d",&l,&r,&x);
printf("%d\n",work(l,r,x));
}
return 0;
}
实现区间众数的查询
LOJ#6285. 数列分块入门 9

思路整理
众数,就是给定一段范围,在这段范围所出现次数最多的数字(如果出现相同次数相同的),那么怎么才能称上是最多,最多是怎么来的?
最多是比较来的,通过每一种数字的数量的比较而来。
那么我们就需要能够算出所有数字在任意给定的区间的数量。
那要怎么做
首先,用vector存好每一个数字在给定区域内所有出现的位置
声明vector
vector<int> g[maxn];
g[x]存放的是值为x在区间的出现的所有的位置的有序序列(实际上是x离散化所得到的下标,我们可以通过另开一个数组去记录x所对应的value,val[x]=i)
但如果这样的话,真的合适吗?(相当于桶排,必然会带来空间的浪费)。
所以应该使用离散化的做法。
而离散化的对象是一个已经存在的数字,
而我们要如何去确定一个数字已经存在呢?
用map或者unordered _map
cin>>a[i];
if(!mp(a[i]))
{
mp[a[i]]=++cnt;//赋予a[i]一个新的下标
val[cnt]=a[i];同时用一个数组存放这个下标对应的值
}
g[mp[a[i]]].push_back(i);
但这里仍然有个问题,也是这道题在LOJ上提交只能得到80分左右的原因。
就是用map(即便是map)取查询一个元素的时候,它所带来的代价并不是O(1),因而当多次使用map或者unordered_map的时候必然会带来一定的时间损耗。
因而这里可以再做一个调整
if (!mp[ A[j] ])
{
mp[ A[j] ] = ++cnt;
val[cnt] = A[j];
}
A[j] = mp[A[j]];
pos[ A[j] ].push_back(j);
方便以后用二分搜索快速找到某个数在区间l到r的所有个数
(在整体区间中找到第一个大于位置r的位置的下标(即便是找到符合条件的,也会往外再跳一个,这样方便到时候不用再去做减一的操作),并以此减去第一个大于或等于位置l的位置的下标,从而获取个数。
int query(int l,int r,int x)
{
greater_bound(g[x].begin(),g[x].end(),r)-lower_bound(g[x].begin(),g[x].end(),l)
}
整体思路
-
预先处理地动态处理好块l到块r的众数
-
然后查l到r的众数,分三个区域来做
-
就是先用l到r区域之间的整块段的众数提取出来扔到二分搜索函数里面跑一遍,得到个数(这个预先存好的众数答案在这个区间段是无敌的)。
-
然后再把左右俩个散块的众数提取出来各跑一遍
-
得到三个答案然后再取最优
80分代码
#include <bits/stdc++.h>
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define pi acos(-1.0)
#define PII pair<int,int>
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 1000000007
#define INF 0x3f3f3f3f
#define lowbit(x) (x&-x)
#define de() cout<<"debug"<<endl;
using namespace std;
const int N = 1e5 + 10, KN = 4E4 + 10, FN = 4005;
int t, blen, n, A[N], bel[N], st[KN], ed[KN], f[FN][FN],cnt[N];
unordered_map<int, int> mp, pcnt;
vector<int> pos[N];
void predo(int x) {
memset(cnt, 0, sizeof(cnt));
int mmax = 0, ans = 0;
for (int i = st[x]; i <= n; i++) {
cnt[ mp[A[i]] ]++;
int p = bel[i];
if (cnt[ mp[A[i]] ] > mmax || (cnt[ mp[A[i]] ] == mmax && ans > A[i])) {
mmax = cnt[ mp[A[i]] ];
ans = A[i];
}
f[x][p] = ans;
}
}
inline int get_num(int l, int r, int x) {
return upper_bound(pos[ mp[x] ].begin(), pos[ mp[x] ].end(), r) - lower_bound(pos[ mp[x] ].begin(),
pos[ mp[x] ].end(), l);
}
inline int ask(int l, int r) {
int res, maxn = 0, val;
if (bel[l] == bel[r]) {
repd(i, l, r) {
int num = get_num(l, r, A[i]);
if (num > maxn || (num == maxn && val > A[i])) {
maxn = num;
val = A[i];
}
}
res = val;
} else {
if (bel[l] + 1 <= bel[r] - 1) {
maxn = get_num(l, r, f[ bel[l] + 1 ][ bel[r] - 1 ]);
val = f[ bel[l] + 1 ][ bel[r] - 1 ];
}
repd(i, l, ed[ bel[l] ]) {
int num = get_num(l, r, A[i]);
if (num > maxn || (num == maxn && val > A[i])) {
maxn = num;
val = A[i];
}
}
repd(i, st[ bel[r] ], r) {
int num = get_num(l, r, A[i]);
if (num > maxn || (num == maxn && val > A[i])) {
maxn = num;
val = A[i];
}
}
res = val;
}
return res;
}
int main() {
cin >> n;
blen = 30;
t = n / blen;
repd(i, 1, t) {
st[i] = (i - 1) * blen + 1;
ed[i] = i * blen;
}
if (ed[t] < n)
t++, st[t] = ed[t - 1] + 1, ed[t] = n;
int cnt = 0;
repd(i, 1, t) {
repd(j, st[i], ed[i]) {
scanf("%d", &A[j]);
if (!mp[ A[j] ])
mp[ A[j] ] = cnt++;
pos[ mp[A[j]] ].push_back(j);
bel[j] = i;
}
}
repd(i, 1, t)
predo(i);
repd(i, 1, n) {
int l, r;
scanf("%d%d", &l, &r);
printf("%d\n", ask(l, r));
}
return 0;
}
100代码
#include <bits/stdc++.h>
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define pi acos(-1.0)
#define PII pair<int,int>
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 1000000007
#define INF 0x3f3f3f3f
#define lowbit(x) (x&-x)
#define de() cout<<"debug"<<endl;
using namespace std;
const int N = 1e5 + 10, KN = 4E4 + 10, FN = 2005;//1e5/80
int t, blen, n, A[N], bel[N], st[KN], ed[KN], f[FN][FN],cnt[N];
ll val[N];
unordered_map<int, int> mp;
vector<int> pos[N];
void predo(int x) {
memset(cnt, 0, sizeof(cnt));
int mmax = 0, ans = 0;
for (int i = st[x]; i <= n; i++) {
cnt[ A[i] ]++;
int p = bel[i];
if (cnt[ A[i] ] > mmax || (cnt[ A[i] ] == mmax && val[ ans ] > val[ A[i] ])) {
mmax = cnt[ A[i] ];
ans = A[i];
}
f[x][p] = ans;
}
}
inline int get_num(int l, int r, int x) {
return upper_bound(pos[ x ].begin(), pos[ x ].end(), r) - lower_bound(pos[ x ].begin(),pos[ x ].end(), l);
}
inline ll ask(int l, int r) {
int maxn = 0, ans;
ll res;
if (bel[l] == bel[r]) {
repd(i, l, r) {
int num = get_num(l, r, A[i]);
if (num > maxn || (num == maxn && val[ans] > val[A[i]] )) {
maxn = num;
ans = A[i];
}
}
res = val[ ans ];
} else {
if (bel[l] + 1 <= bel[r] - 1) {
maxn = get_num(l, r, f[ bel[l] + 1 ][ bel[r] - 1 ]);
ans = f[ bel[l] + 1 ][ bel[r] - 1 ];
}
repd(i, l, ed[ bel[l] ]) {
int num = get_num(l, r, A[i]);
if (num > maxn || (num == maxn && val[ans] > val[ A[i] ])) {
maxn = num;
ans = A[i];
}
}
repd(i, st[ bel[r] ], r) {
int num = get_num(l, r, A[i]);
if (num > maxn || (num == maxn && val[ans] > val[ A[i] ])) {
maxn = num;
ans = A[i];
}
}
res = val[ ans ];
}
return res;
}
int main() {
cin >> n;
blen = 80;
t = n / blen;
repd(i, 1, t) {
st[i] = (i - 1) * blen + 1;
ed[i] = i * blen;
}
if (ed[t] < n)
t++, st[t] = ed[t - 1] + 1, ed[t] = n;
int cnt = 0;
repd(i, 1, t) {
repd(j, st[i], ed[i]) {
scanf("%d", &A[j]);
if (!mp[ A[j] ])
{
mp[ A[j] ] = ++cnt;
val[cnt] = A[j];
}
A[j] = mp[A[j]];
pos[ A[j] ].push_back(j);
bel[j] = i;
}
}
repd(i, 1, t)
predo(i);
repd(i, 1, n) {
int l, r;
scanf("%d%d", &l, &r);
printf("%lld\n", ask(l, r));
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号