【数据结构】树状数组
树状数组
引入1
给出一个长度为n的数组,完成以下两种操作:
- 将第x个数加上k(对应的是单点修改)
- 输出区间[x,y]内每一个数的和(对应的是区间查询)
朴素的做法
- 操作一是只需直接对a[i]的值进行单点修改,这是一个\(O(1)\)的操作,而操作二就需要对区间内每一个元素进行访问并累加它们的值,这是一个\(O(n)\)的操作,而如果执行了n次操作二,就需要一个\(O(n^{2})\)的复杂度,这种复杂度是相对较大的,因而要避免直接去使用朴素的做法。
树状数组
- 而对于树状数组来说,操作一和操作二的时间复杂度都是\(O(log_{2}n)\)级别的,而使用n次的操作二将会带来\(O(nlog_{2}n)\)级别的复杂度,相对于\(O(n^{2})\) 就优秀了很多。
引入2
众所周知,我们可以将一个数(十进制数下)转成一个二进制的数,比如十进制的数x可以在二进制的表达下变成\(a_{k-1}a_{k-2}...a_1a_0\),而不妨把起其中\(a_{i}=1\)的位置从左到右给抓起来,并组成一个新的序列,记为\({a_{i_{1}},a_{i_{2}},a_{i_{3}},...a_{i_{m}}}\),且\(x=2^{i_{1}}+2^{i_{2}}+...+2^{i_{m}}\),且\(i_1>i_2>...>i_m\)
注意到从\(2^{i_{1}}\)到\(2^{i_{1}}+2^{i_{2}}\)有一段叫做\(2^{i_{2}}\)的距离
注意到从\(2^{i_{1}}+2^{i_{2}}\)到\(2^{i_{1}}+2^{i_{2}}+2^{i_{3}}\)有一段叫做\(2^{i_{3}}\)的距离
而树状数组恰恰是利用了这一特性
将一个大区间,按这个大区间的区间长度,通过以上的二进制转化方法,来进行拆分,从而得到\(logX\)的小区间,且每个小区间的区间长度为\(2^{i_{k}}\)
比如可以依次得到
长度为\(2^{i_1}\)的\([1,2^{i_{1}}]\),
长度为\(2^{i_2}\)的\([2^{i_1}+1,2^{i_{1}}+2^{i_2}]\),
...,
长度为\(2^{i_{m}}\)的\([2^{i_{1}}+2^{i_2}+...+2^{i_{m-1}}+1\),\(2^{i_{1}}+2^{i_2}+...+2^{i_{m-1}}+2^{i_m}]\)
比如拿15来举例子,\(15=2^{3}+2^{2}+2^{1}+2^{0}\),\(15\)可以分成\([1,8],[9,12],[13,14],[15,15]\)四个小区间
while(x>0)
{
printf("[%d, %d]\n",x-(x&-x)+1,x);
x-=x&-x;
}
注意到上述代码中出现了两次x&-x;注意到这些区间的区间长度相当于对这些区间的右端点所代表的值取lowbit操作。
而为什么要写x&-x,而什么是lowbit操作呢?
(x代表的是x的原码,~x代表的是x的反码,-x代表的是x的补码,&代表的是与运算)
lowbit(x)操作就是得到当前数字(非负整数)在二进制表示下最低位1及其后面的0构成的数值。
比如\(lowbit(34)=lowbit(|10010|_{2})=|10|_{2}=2\)
那我们要怎么样才能够实现lowbit操作呢?
只需要用一个数去与上另一个数的补码,那为啥是这个样子呢?
众所周知,一个数的补码等于一个数的反码+1,而一个正数的反码是将最高位(符号位)置为1且保持它不变,其他位进行翻转(原本的0变成1,原本的1变成0),如果可以的话会发现反码的右侧多了一连串的1,而这时只要再对整个反码再加上1,就会发现这些1要直到向右遇到一个0才能消停,且把这个0置为1,注意这个0的位置,其实对应到原码的位置上的数字是1(因为翻转了嘛),而刚才那些反码位置上的1其实是原码的0,而这个特殊的1的位置的左边是没有“动过刀”的(虽然是补码的部分,但其实可以看成是反码的部分)。故而操作是可行的。
比如34的原码是0001 0010 ,反码是1110 1101 ,补码是1110 1110,34的原码与上补码是0000 0010.
int lowbit(int x)
{
return x&(-x);
}
树状数组
树状数组思想及其实现
树状数组所支持的基本操作
区间查询/查询前缀和
区间查询\(\Rightarrow\)区间和\(\Rightarrow\)前缀和
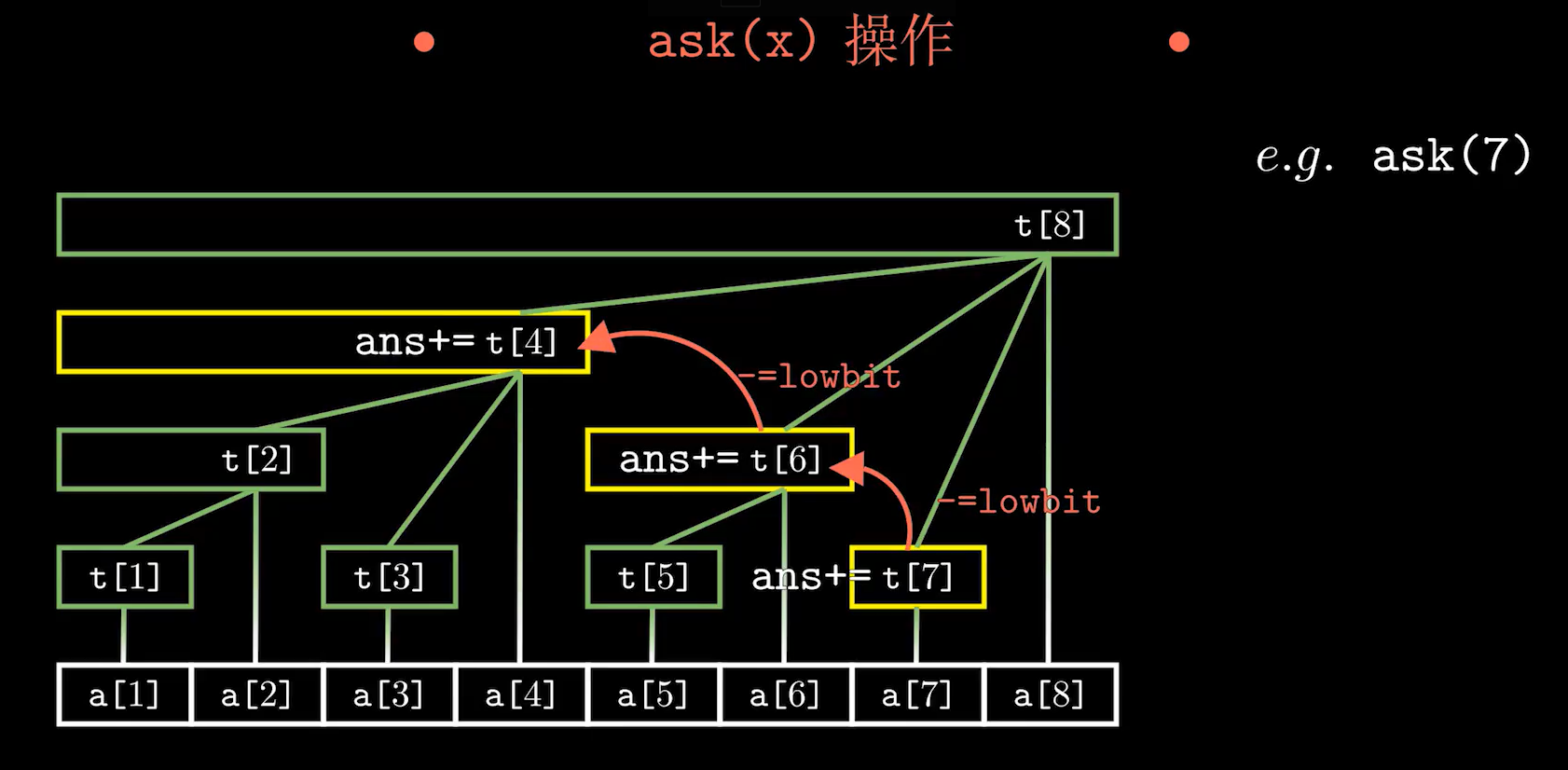
int ask(int x)
{
int ans=0;
//for(;x;x-=x&(-x))ans+=c[x];
for(;x;x-=lowbit(x))ans+=c[x];
return ans;
}
单点增加
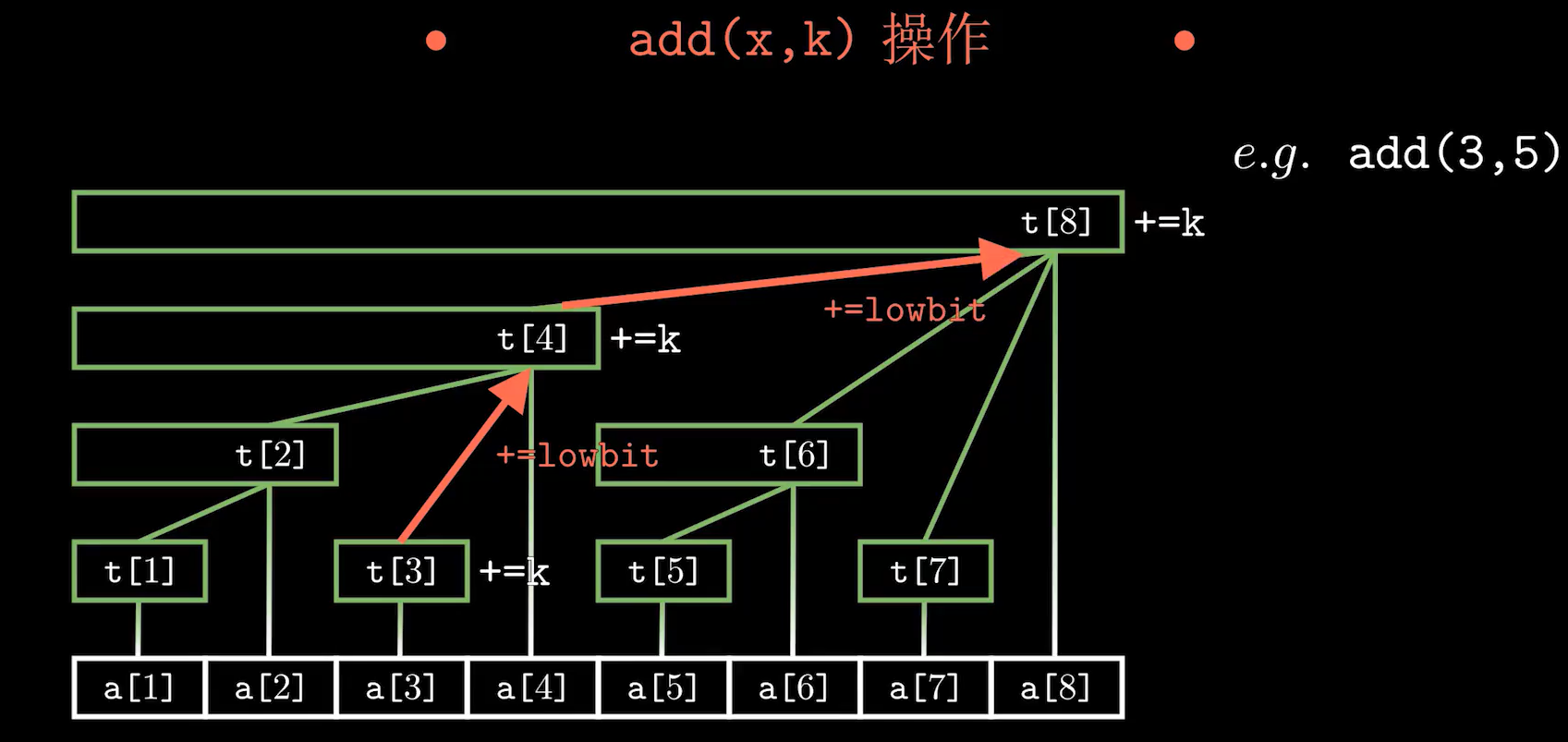
void add(int x,int y)
{
for(;x<=N;x+=x&(-x))c[x]+=y;
}
树状数组与逆序对
逆序对
设 A 为一个有 n 个数字的有序集 (n>1),其中所有数字各不相同。
如果存在正整数 i, j 使得 1 ≤ i < j ≤ n 而且 A[i] > A[j],则 <A[i], A[j]> 这个有序对称为 A 的一个逆序对,也称作逆序数。
逆序对就是指一个数拥有相对于另一个数较小的位置却拥有较大的数值,并且由这两个数共同组成的一对数。
树状数组在处理逆序对的问题时是一个动态的过程,流程大致是从左到右,用树状数组的sum函数查询出比当前位置上的数字还大的数字的数量。并且将当前数字用树状数组特有的add函数添加到t数组中去。
AcWing 241. 楼兰图腾
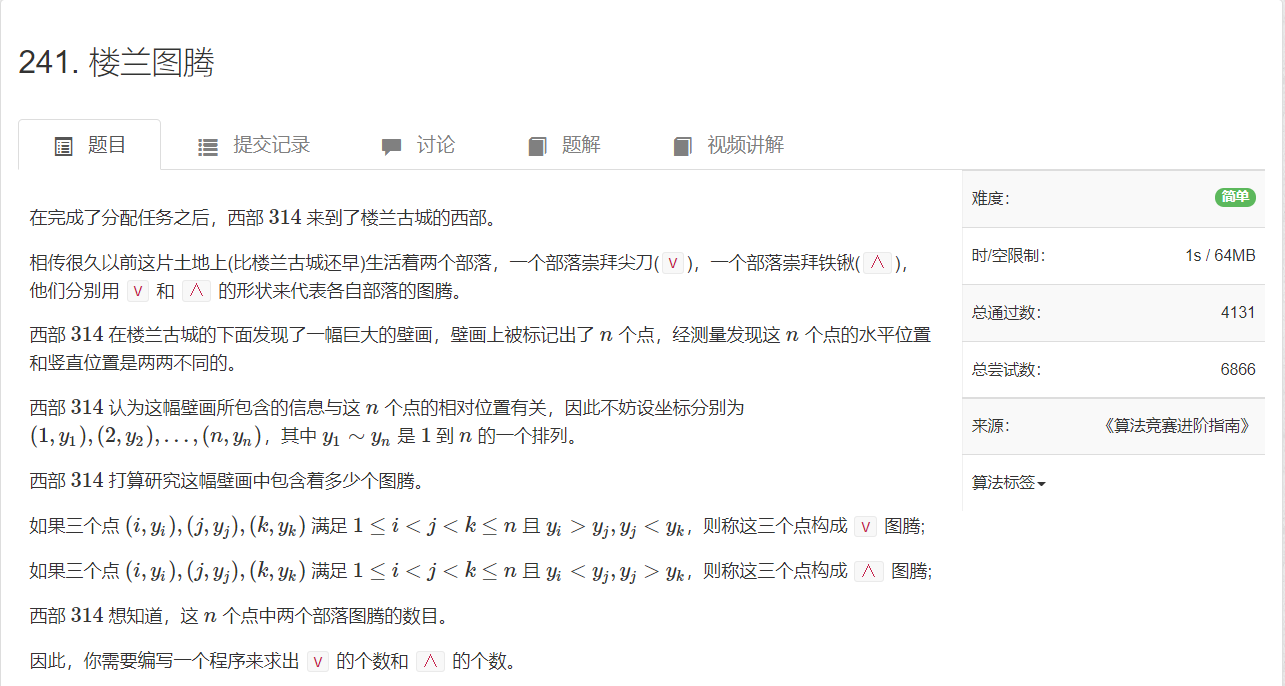
思路:流程是从左到右,查询出比当前位置上的数字还大的数字的数量(左边),记录到一个数组中去,并且也要查询出比当前位置上的数字还小的数字的数量(左边),记录到另外一个数组中去,然后在清空t数组,从右到左扫一遍,分别查询出比当前位置上的数字还大的数字的个数(右边)和比当前位置上的数字还小的数字的个数(右边),并且利用前面已经处理好的数组,就可以得到答案。
#include <bits/stdc++.h>
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define pi acos(-1.0)
#define PII pair<int,int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 1000000007
#define INF 0x3f3f3f3f
using namespace std;
int const N = 2E5+10;
int n,m;
ll t[N],up[N],down[N],a[N];
ll lowbit(int x)
{
return x&(-x);
}
void add(int x,int k)
{
for(;x<=N;x+=lowbit(x)) t[x]+=k;
}
ll sum(int x)
{
ll total=0;
for(;x;x-=lowbit(x)) total+=t[x];
return total;
}
int main()
{
cin>>n;
repd(i,1,n)
{
cin>>a[i];
up[i]=sum(N)-sum(a[i]);
down[i]=sum(a[i]-1);
add(a[i],1);
}
memset(t,0,sizeof(t));
ll resV=0,resA=0;
for(int i=n;i>=1;i--)
{
resV+=( sum(N)-sum(a[i]) )*up[i];
resA+=sum(a[i]-1)*down[i];
add(a[i],1);
}
cout<<resV<<" "<<resA;
return 0;
}
树状数组与差分
首先明确一点树状数组只是用来维护数组前缀和的工具,至于维护的是什么样的数组和树状数组并没有很大的关系。
差分,什么是差分?
就比如说有一群人,张三有100块钱,赵四自己也有些钱,但只记得比张三多了5块钱,但懒得记自己有多少钱,郝建自己也有些钱,但只记得比赵四少了13块钱。
差分数组,就是把差价记住,然后根据某一个记忆点,利用这些记住的差价将原本的数据进行还原。
-
那如果差价为0,就代表后者与前者具有相同的值。(这是一种较为静态的思想)
那有没有什么操作能够实现前者与后者具有相同的值?
具有相同的值的一连串的数字同时加上或减上相同的数字(其他情况暂时不去考虑,或者说缺乏价值去讨论)
而这必然会导致这一连串的数字的第一个数字和其前一个的数字差上一个新的值,也会导致这一连串的数字的最后一个数字和其后一个的数字差上一个新的值。
你可以想象一个画面,就是地震了,两边的地势突然往中间挤压,突然抬高了一片平地,或者中间突然塌方,导致中间地带和两边存在一定的差值。
-
而进一步的话,你可以将这一串数字数字两两差价为0的条件给屏蔽掉(差价为0和操作之间并没有很大的关系,只是为了起初理解的方便)。
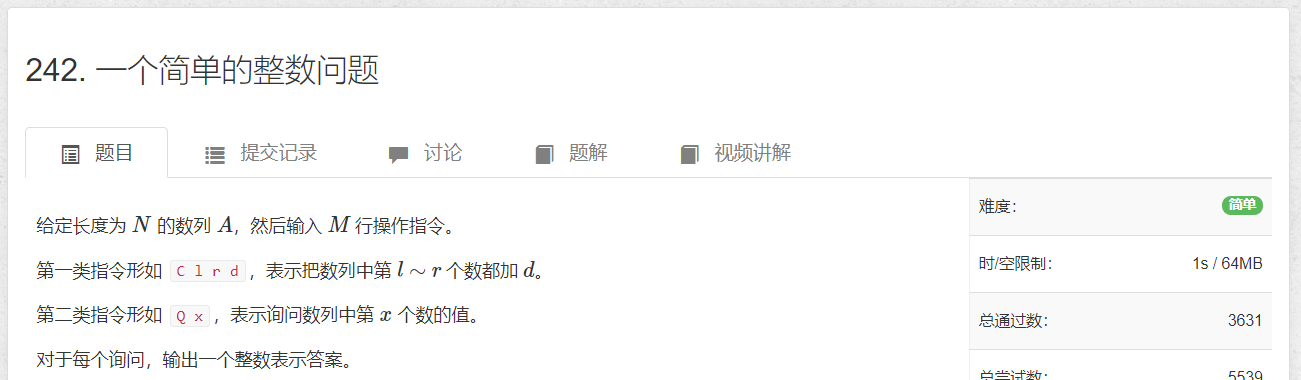
AcWing 242. 一个简单的整数问题
#include <bits/stdc++.h>
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define pi acos(-1.0)
#define PII pair<int,int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 1000000007
#define INF 0x3f3f3f3f
using namespace std;
const int N = 1e5+10;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
int n,m;
int t[N];
ll lowbit(int x)
{
return x&-x;
}
void add(int x,int k)
{
for(;x<=n;x+=lowbit(x)) t[x]+=k;
}
ll sum(int x)
{
ll res=0;
for(;x;x-=lowbit(x)) res+=t[x];
return res;
}
int main()
{
cin>>n>>m;
ll x,a[n+1];
a[0]=0;
repd(i,1,n)
{
cin>>a[i];
add(i,a[i]-a[i-1]);//会对整个差分数组的部分造成影响,但sum运算的过程中有单次的影响
//第i个位置,加上差分的量
}
repd(i,1,m)
{
char c;
cin>>c;
if(c=='C')
{
int l,r,d;
cin>>l>>r>>d;
add(l,d);
add(r+1,-d);
}
else if(c=='Q')
{
int x;
cin>>x;
cout<<sum(x)<<endl;
}
}
return 0;
}
AcWing 243. 一个简单的整数问题2
对于一个简单的整数问题1,求单个数,只需要对差分数组求一个前缀和就行,\(a[k]=\sum _{i=1}^{k}d[i]\),而这时我们要求的一个区间l到r(这里做一个简单的处理,利用前缀和的思想,我们不妨先去求区间1到r)的数字之和即,\(\sum_{k=1}^{r}\sum_{i=1}^{k}d[i]=\sum_{i=1}^r(r-i+1)\times d[i]=\sum_{i=1}^r(r+1)\times d[i]-\sum_{i=1}^{r}i\times d[i]\\= (r+1)\times\sum_{i=1}^r d[i]-\sum_{i=1}^{r}i\times d[i]\)
所以要开两个树状数组或者一个二维的树状数组去分别维护\(d[i]\)和\(i\times d[i]\)
关于维护\(i\times d[i]\)的想法
差分数组每一个元素都是指的是后一个元素减去前一个元素的差值,而区间加减内的每一个元素前后的差值都是0,也就意味着差分数组无论是乘上任何数字最终的结果都是0,所以只需要考虑跟区间两旁的元素的关系就行
#include <bits/stdc++.h>
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define pi acos(-1.0)
#define PII pair<int,int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 1000000007
#define INF 0x3f3f3f3f
#define lowbit(x) (x&-x)
using namespace std;
const int N = 1e5+10;
ll n,m,a[N],t[2][N];
void add(int op,ll x,ll k)
{
for(;x<=n;x+=lowbit(x)) t[op][x]+=k;
}
ll sum(int op,ll x)
{
ll res = 0;
for(;x;x-=lowbit(x))res+=t[op][x];
return res;
}
ll compute(ll x)
{
return (x+1)*sum(0,x)-sum(1,x);
}
int main()
{
cin>>n>>m;
a[0]=0;
repd(i,1,n)
{
cin>>a[i];
add(0,i,a[i]-a[i-1]);
add(1,i,i*(a[i]-a[i-1]));
}
repd(i,1,m)
{
char q;
cin>>q;
if(q=='C')
{
ll l,r,d;
cin>>l>>r>>d;
add(0,l,d);add(0,r+1,-d);
add(1,l,l*d);add(1,r+1,-(r+1)*d);
}
else if(q=='Q')
{
ll l,r;
cin>>l>>r;
cout<<compute(r)-compute(l-1)<<endl;
}
}
return 0;
}
参考
鹤翔万里,B站大佬
+蓝书


 浙公网安备 33010602011771号
浙公网安备 33010602011771号