【数学】矩阵乘法【CF】D. Magic Gems

目录

• 矩阵乘法
  • 矩阵乘法的定义
  • 矩阵乘法的特殊情形
    • 应用
      • 实现
  • AcWing 205. 斐波那契
• 其他
  • 单位矩阵
  • memcpy函数
  • 矩阵乘法的优化

矩阵乘法

矩阵乘法顾名思义，就是将两个矩阵做乘法运算（相当于在矩阵意义下重载乘法运算符？）

矩阵乘法的定义

矩阵A $\times $​ 矩阵B = 矩阵C

\[C_{i,j}=\sum_{k=1}^{m}A_{i,k}\times B_{k,j} \]

矩阵C的第i行第j列元素是矩阵A第i行的所有元素与矩阵B的第j列的所有元素对应相乘的乘积的总和。

• 对应就要求矩阵A的列数要等于矩阵B的行数。

• 即A是\(M\times N\)的矩阵，B是\(N\times K\)的矩阵

同时矩阵乘法，满足结合律，分配律，但不满足交换律（一是最终形成的矩阵的行数和列数不一定一样，即便是一样，矩阵里的数据也不一定一样）。

矩阵乘法的特殊情形

矩阵A是一个\(N\times N\)​的矩阵，矩阵F是一个\(N\times 1\)​的矩阵,设\(F_{1}=A\times F\)​，发现\(F_{1}\)​也是一个\(N\times 1\)​的矩阵，是一个有只有一列元素的元素，我们不妨把这些元素看成是一个个变量，而矩阵\(F_{1}\)​ 的变量是通过矩阵\(F\)​的变量的某种关系来实现更新，而这种关系是记录到矩阵A里面的（所以矩阵A也可以称作是系数矩阵？）

• 有将一维度的矩阵F定义为状态矩阵，并将不变且用来相乘的矩阵A称作转移矩阵。

比如斐波那契数列，\(F_{n+2}=F_{n+1}+F_{n}\)​​,在不考虑对所有的\(F_{i}\)​​的值就进行记录时，即\(\begin{cases} F_{n+2}=F_{n+1}+F_{n}\\F_{n+1}=F_{n+1}\end{cases}\)​​在空间上进行优化可优化为，\(\begin{cases} F_{n+1}=F_{n+1}+F_{n}\\F_n=F_{n+1}\end{cases}\)​​，转化为矩阵算法有\(\begin{bmatrix} F_{n+1}&F_{n} \end{bmatrix}=\begin{bmatrix} F_{n+1}&F_{n} \end{bmatrix}\times \begin{bmatrix} 1&1\\1&0 \end{bmatrix}\)​​

应用

上述的矩阵乘法的特殊情形常用于递推式，特别是当递推的层次达到一定的数量级，就可以用矩阵快速幂来减少计算次数，优化计算速度，从而提高效率，而一般的递推只能重复性的计算（和覆盖）。

实现

• 矩阵C的第i行第j列元素是矩阵A第i行的所有元素与矩阵B的第j列的所有元素对应相乘的乘积的总和。

  for(int i=0;i<N;i++)
     for(int j=0;j<K;j++)//合成完后是一个N*K的矩阵
         for(int k=0;k<M;k++)
             C[i][j]+=A[i][k]*B[k][j];
  

• 而如果要从\(F_{1}\)出发来得到\(F_{N}\),能不能有一种方法来减少计算量呢？

• 发现\(F_{N}=A\times F_{N-1}=A^{N}\times F_{0}\)​（由递推得到）​

• A的n次方是否要一个一个A来连乘来获得？是否有什么方法来快速得到答案？

• 快速幂？！矩阵快速幂？！于是这块运算的级别就可以从\(O(N)\)​级别降低到 \(O(logN)\)​​​级别，最终再乘上内部单轮矩阵乘法共需要的时间（三重循环）来得到最终的复杂度。

• 代码框架

定义一个存放矩阵的结构体
struct Mat{
     ll mat[110][110];
     Mat() {}
     //结构体内重载运算符
     Mat operator*(Mat const &b)const
     {
          Mat res;
          memset(res.mat,0,sizeof(res.mat));
          for(int i=0;i<maxn;i++)
              for(int j=0;j<maxn;j++)
                  for(int k=0;l<maxn;k++)
                     res.mat[i][j]=(res.mat[i][j]+this->mat[i][k]*b.mat[k][j]);
          return res;
     }

}

定义一个返回类型为mat的，作用为实现矩阵快速幂的函数
Mat pow_mod(Mat base,ll n)
{
      Mat res;
      memset(res,0,sizeof(res));
      for(int i=0;i<maxn;i++) //定义一个单位矩阵
          res.mat[i][i] = 1;
      while(n>0)
      {
          if(n&1)res=res*base;
          base=base*base;
          n>>=1;
      }
      return res;
}

AcWing 205. 斐波那契

#include <bits/stdc++.h>
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define pi acos(-1.0)
#define PII pair<int,int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 10000
#define INF 0x3f3f3f3f
#define lowbit(x) (x&-x)
using namespace std;
int n,m;
void mul(int f[2],int A[2][2])//f[1][2]
{
	int C[2];//C[1][2]
	memset(C,0,sizeof(C));
	for(int j=0;j<2;j++)
	    for(int k=0;k<2;k++)
            C[j]=(C[j]+(ll)f[k]*A[k][j])%MOD;//C[i]相当于是C的第一行的第i个元素 
    memcpy(f,C,sizeof(C)); 
}    
void mulself(int A[2][2])
{
	int C[2][2];
	memset(C,0,sizeof(C));
	for(int i=0;i<2;i++)
	    for(int j=0;j<2;j++)
	        for(int k=0;k<2;k++)
	            C[i][j]=(C[i][j]+(ll)A[i][k]*A[k][j])%MOD;
	memcpy(A,C,sizeof(C));            
}
int main()
{ 
    while(cin>>n && n!=-1)
    {
    	int f[2] = {0,1};
    	int A[2][2]={
		                {0,1},
		                {1,1}
		            };
		while(n>0)
		{
			if(n&1)mul(f,A);
			mulself(A);
			n=n>>1;
		}
		cout<<f[0]<<endl;
	}
    return 0;
}

D. Magic Gems

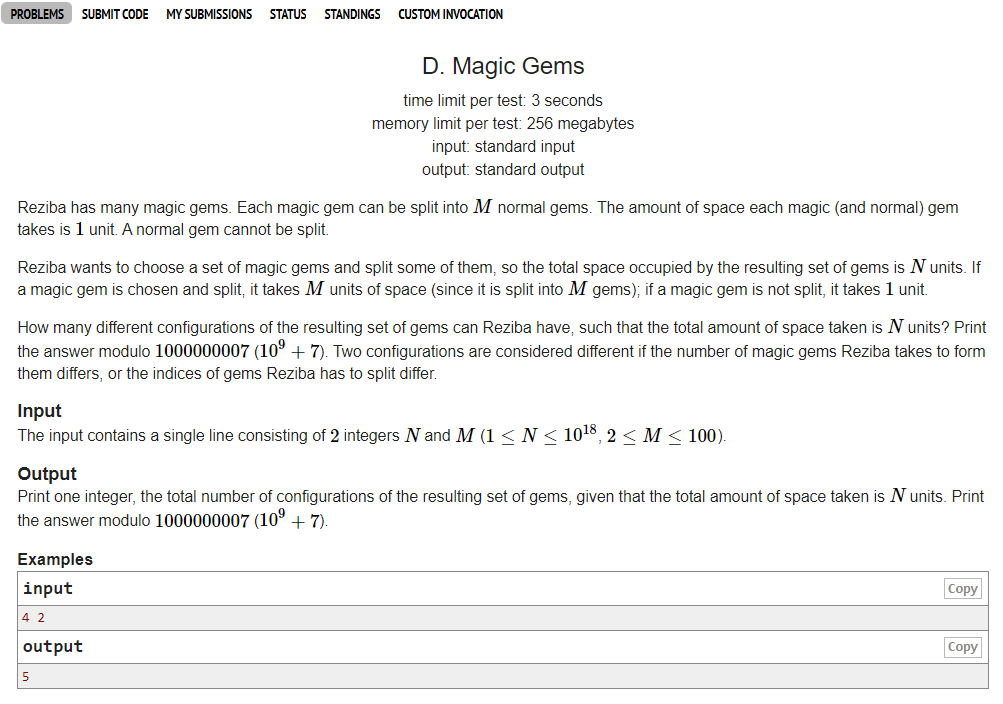
题意：

Reziba拥有许多神奇的宝石。每一颗魔法石都可以切分成M块普通石头。从占用的角度上来说，无论是神奇的宝石还是普通的宝石都会占据一个单位的空间，并且普通的宝石无法继续切割。

Rezilba想要选择一套魔法石并且切割其中的一部分，以至于最终这些宝石能够占用到N个单位空间。如果神奇的宝石有被切割成M份，那就当做是占据了M个空间，否则还是当做只占用了一个空间。

给定一个数字N和M，N是最终构成的宝石数目，M是普通宝石和神奇宝石的比值。请问在这种转换比的条件下，有多少种方案能到达N颗。

补题思路：

要达到刚刚好占用n个空间有两种办法，一种是在已经占用了n-1个空间的时候再添置一个普通宝石，另一种的方法是在已经占用n-m个空间的时候，释放一颗魔法石，来占用m个空间。

f[n]=f[n-1]+f[n-m];仅当n>=m时，否则的话f[n]=f[n-1];

\[\begin{pmatrix}f_{n}\space 0\space 0....0\\f_{n-1}\space 0\space 0...0\\f_{n-2}\space 0\space 0...0\\.\\.\\f_{n-m+1} \space 0\space 0.0\end{pmatrix} = \begin{pmatrix} 1 \space 0\space 0....1\\1\space 0\space0....0\\0\space 1\space0....0\\........\\........\\......1\space0\end{pmatrix} \times \begin{pmatrix}f_{n-1}\space 0\space 0....0\\f_{n-2}\space 0\space 0....0\\f_{n-3}\space 0\space 0....0\\.\\.\\f_{n-m}\space 0\space 0....0 \end{pmatrix} \]

#include <bits/stdc++.h>
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define pi acos(-1.0)
#define PII pair<int,int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 1000000007
#define INF 0x3f3f3f3f
#define lowbit(x) (x&-x)
using namespace std;
ll n;int m; 
struct Mat{
	ll mat[110][110];
	Mat(){};
	Mat operator*(Mat const &b)const
	{
		Mat res;
		memset(res.mat,0,sizeof(res.mat));
		rep(k,0,m)
		   rep(i,0,m)
		       rep(j,0,m)
		          res.mat[i][j]=(res.mat[i][j]+(this->mat[i][k]*b.mat[k][j]))%MOD;
		return res;    
	}
};

Mat mat_pow(Mat A,ll k)
{
	Mat res;
	memset(res.mat,0,sizeof(res.mat));
    rep(i,0,m)
        res.mat[i][i]=1;
    while(k>0)
    {
    	if(k&1)res=res*A;
    	A=A*A;
    	k=k>>1;
	}
	return res;
}
int main()
{
	Mat base,A;
	scanf("%lld%d",&n,&m);//注意n是lld 
	if(n<m)
	{
		printf("1\n");
		return 0;
	}
	memset(base.mat,0,sizeof(base.mat));
	memset(A.mat,0,sizeof(A.mat));
	A.mat[0][0]=1,A.mat[0][m-1]=1;
	rep(i,1,m)
	    A.mat[i][i-1]=1;
	rep(i,0,m)
	    base.mat[i][0]=1;
	A=mat_pow(A,n-m+1);
	base=A*base;
	printf("%lld",base.mat[0][0]);//在乘法的过程中已经做过了取余 
    return 0;
}

其他

单位矩阵

一个矩阵乘上单位矩阵后保持不变（前提是能够相乘）

memcpy函数

• C 库函数 void *memcpy(void *str1, const void *str2, size_t n) 从存储区 str2 复制 n 个字节到存储区 str1。

矩阵乘法的优化

采取k，i，j的三重循环顺序相比于i，j，k能提高cache的命中率，从而提高运行效率。