造树计划——线段树
线段树
错误纪念
线段树原理
- 线段树通过树上的各个节点来保存子线段的信息,比如左右端点和一些特殊的值(区间和等等)
- 懒惰标记lazy_tag:相当于在一个节点上不断蓄势,而暂时不去考虑变化这个节点的子节点的信息。从而达到偷懒的效果。(能节省出大量的时间)
结点信息
-
区间左右端点
-
懒标记
-
区间和
struct{ ll l,r; ll lazy,sum; }
操作
-
建树build
- 当前结点的位置、左坐标、右坐标
- 分两种情况
- 找到单个点
- 找到的是区间,如果是区间的话,向左向右拆成两部分(这里是需要不断对l和r进行修改的)
void build(ll u,ll l,ll r) { tree[u]={l,r,0,0}; if(l==r) { tree[u]=arr[l]; } ll mid = l+r>>1 build(u<<1,l,mid); build(u<<1|1,mid+1,r); tree[u]=tree[u<<1]+tree[u<<1|1]; } -
下放懒标记push_down(囤货的意识)
- 两个方向的下放
- 向左子树下放
- 向右子树下放
void push_down(int u) { 子节点获取父节点的相关信息 tree[u].lazy=0;//消除父节点的懒惰标记 } - 两个方向的下放
-
向上更新点的和push_up
- 注意push_up的操作是在push_down的操作后面,因为必须先解决下方的区间和,才能处理好上面根节点的和
void push_up(int u) { tree[u]=tree[u<<1]+tree[u<<1|1]; } -
修改区间和(加法)=区间长度*单位增量
-
这里是不需要对l和r进行修改的,因为你随时都需要一个明确的区间,来使得树上节点所代表的区间不断加入到这个明确的区间中去
void modify_add(ll u,ll l,ll r,ll k) { if(tree[u].l>=l&&tree[u].r<=r) { tree[u].sum+=(tree[u].r-tree[u].l+1)*k; tree[u].lazy_add+=k; } else { push_down(u); ll mid = tree[u].l+tree[u].r>>1; if(mid>=l)modify_add(u<<1,l,r,k); if(mid+1<=r)modify_add(u<<1,l,r,k); push_up(u); } }
练习题
模板题
1模板题1传送门
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
#define ll long long
ll n,m,a[N];
struct Node{
ll l,r;
ll lazy,sum;
}tr[N<<2];
void push_up(ll u){
tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}
void build(ll u,ll l,ll r){
tr[u]={l,r,0,0};
if(l==r&&l==tr[u].r){
tr[u].sum=a[l];
}
else {
int mid=l+r>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
push_up(u);
}
}
void push_down(int u){
tr[u<<1].sum+=tr[u].lazy*(tr[u<<1].r-tr[u<<1].l+1);
tr[u<<1].lazy+=tr[u].lazy;
tr[u<<1|1].sum+=tr[u].lazy*(tr[u<<1|1].r-tr[u<<1|1].l+1);
tr[u<<1|1].lazy+=tr[u].lazy;
tr[u].lazy=0;
}
void modify(int u,int l,int r,ll k){
if(tr[u].l>=l&&tr[u].r<=r){
tr[u].sum+=k*(tr[u].r-tr[u].l+1);
tr[u].lazy+=k;
}
else{
int mid=(tr[u].l+tr[u].r)>>1;
push_down(u);
if(l<=mid)modify(u<<1,l,r,k);
if(r>mid)modify(u<<1|1,l,r,k);
push_up(u);
}
}
ll query(int u,int l,int r){
if(tr[u].l>=l&&tr[u].r<=r)return tr[u].sum;
else {
ll res=0;
ll mid=(tr[u].l+tr[u].r)>>1;
push_down(u);
if(l<=mid)res+=query(u<<1,l,r);
if(r>mid)res+=query(u<<1|1,l,r);
return res;
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>a[i];
build(1,1,n);
while(m--){
//for(int i=1;i<=n<<2;i++)cout<<tr[i].sum<<' ';
ll k;
cin>>k;
if(k==1){
ll l,r;
cin>>l>>r>>k;
modify(1,l,r,k);
}
else {
ll l,r;
cin>>l>>r;
cout<<query(1,l,r)<<endl;
}
}
return 0;
}
2.模板题2传送门
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1E5+10;
struct Node{
int l,r;
int sum,lazy_mul,lazy_add;
}tree[N];
int arr[N];
int n,m,MOD;
void push_down(ll u)
{
tree[u<<1].sum+=(tree[u<<1].sum*tree[u].lazy_mul+(tree[u<<1].r-tree[u<<1].l+1)*tree[u].lazy_add)%MOD;
tree[u<<1].lazy_mul*=tree[u].lazy_mul%MOD;
tree[u<<1].lazy_add+=(tree[u<<1].lazy_add*tree[u].lazy_mul+tree[u].lazy_add)%MOD;
tree[u<<1|1].sum+=(tree[u<<1|1].sum*tree[u].lazy_mul+(tree[u<<1|1].r-tree[u<<1|1].l+1)*tree[u].lazy_add)%MOD;
tree[u<<1|1].lazy_mul*=tree[u].lazy_mul;
tree[u<<1|1].lazy_add+=tree[u<<1|1].lazy_add*tree[u].lazy_mul+tree[u].lazy_add;
tree[u].lazy_mul=1;
tree[u].lazy_add=0;
}
void push_up(ll u)
{
tree[u].sum+=(tree[u<<1].sum+tree[u<<1|1].sum)%MOD;
}
void build_tree(ll u , ll l ,ll r)
{
tree[u]={l,r,0,1,0};
if(l==r)
{
tree[u].sum=arr[l];
}
else
{
ll mid = l+r>>1;
build_tree(u<<1,l,mid);
build_tree(u<<1|1,mid+1,r);
push_up(u);
}
}
void modify_add(ll u,ll l,ll r,ll k)
{
if(tree[u].l>=l&&tree[u].r<=r)
{
tree[u].sum+=(tree[u].r-tree[u].l+1)*k;
tree[u].lazy_add+=k;
}
else
{
push_down(u);
ll mid = tree[u].l+tree[u].r>>1;
if(mid>=l)modify_add(u<<1,l,mid,k);
if(mid+1<=r)modify_add(u<<1,mid+1,r,k);
push_up(u);
}
}
void modify_mul(ll u,ll l,ll r,ll k)
{
if(tree[u].l>=l&&tree[u].r<=r)
{
tree[u].sum+=tree[u].sum*k;
tree[u].lazy_add*=k;
tree[u].lazy_mul*=k;
}
else
{
push_down(u);
ll mid = tree[u].l+tree[u].r>>1;
if(mid>=l)modify_mul(u<<1,l,mid,k);
if(mid+1<=r)modify_mul(u<<1|1,mid+1,r,k);
push_up(u);
}
}
ll query(ll u, ll l ,ll r)
{
if(tree[u].l>=l&&tree[u].r<=r)
{
return tree[u].sum;
}
else
{
ll res = 0;
ll mid = tree[u].l+tree[u].r>>1;
push_down(u);//没有办法整段加和,必须下放
if(l<=mid)res+=query(u<<1,l,r);//有必要搜索
if(mid<r)res+=query(u<<1|1,l,r); //有必要搜索
return res;
}
}
int main()
{
cin>>n>>m>>MOD;
for(int i = 1 ;i<=n;i++)
{
cin>>arr[i];
}
build_tree(1,1,n);
for(int i = 1;i<=m;i++)
{
int oper;
cin>>oper;
int x,y,k;
if(oper==1)
{
cin>>x>>y>>k;
modify_add(1,x,y,k);
}
else if(oper==2)
{
cin>>x>>y>>k;
modify_mul(1,x,y,k);
}
else if(oper==3)
{
cin>>x>>y;
cout<<query(1,x,y);
}
}
return 0;
}
一般的题目
P2574 XOR的艺术
#include<bits/stdc++.h>
using namespace std;
const int N = 2*1e5+10;
#define ll long long
string s;
ll n,m;
struct NODE{
ll l,r;
ll sum_0,sum_1,lazy_change;
}tree[N<<2];
void resverse(ll u)
{
ll t=tree[u].sum_1;
tree[u].sum_1=tree[u].sum_0;
tree[u].sum_0=t;
}
void push_down(ll u)
{
if(tree[u].lazy_change==1)
{
resverse(u<<1);resverse(u<<1|1);
tree[u<<1].lazy_change=(tree[u<<1].lazy_change+tree[u].lazy_change)%2;
tree[u<<1|1].lazy_change=(tree[u<<1|1].lazy_change+tree[u].lazy_change)%2;
}
tree[u].lazy_change=0;
}
void push_up(ll u)
{
tree[u].sum_0=tree[u<<1].sum_0+tree[u<<1|1].sum_0;
tree[u].sum_1=tree[u<<1].sum_1+tree[u<<1|1].sum_1;
}
void build_tree(ll u,ll l,ll r)
{
tree[u]={l,r,0,0,0};
if(l==r)
{
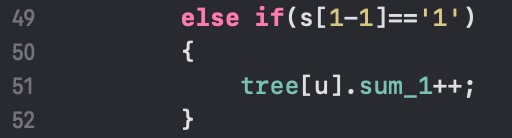
if(s[l-1]=='0')
{
tree[u].sum_0++;
}
else if(s[l-1]=='1')
{
tree[u].sum_1++;
}
}
else
{
ll mid=l+r>>1;
build_tree(u<<1,l,mid);
build_tree(u<<1|1,mid+1,r);
push_up(u);
}
}
void modify_resverse(ll u,ll l,ll r)
{
if(tree[u].l>=l&&tree[u].r<=r)
{
resverse(u);//直接反转
tree[u].lazy_change=tree[u].lazy_change^1;
}
else
{
ll mid = tree[u].l+tree[u].r>>1;
push_down(u);
if(mid>=l)modify_resverse(u<<1,l,r);
if(mid+1<=r)modify_resverse(u<<1|1,l,r);
push_up(u);
}
}
ll query(ll u,ll l,ll r)
{
if(tree[u].l>=l&&tree[u].r<=r)
{
return tree[u].sum_1;
}
else
{
push_down(u);
ll mid=tree[u].l+tree[u].r>>1;
ll res=0;
if(mid>=l)res+=query(u<<1,l,r);
if(mid+1<=r)res+=query(u<<1|1,l,r);
push_up(u);
return res;
}
}
int main()
{
cin>>n>>m>>s;
build_tree(1,1,n);
int oper,x,y;
for(int i=1;i<=m;i++)
{
cin>>oper;
if(oper==0)
{
cin>>x>>y;
modify_resverse(1,x,y);
}
else if(oper==1)
{
cin>>x>>y;
cout<<query(1,x,y)<<endl;
}
}
return 0;
}
感谢
感谢黄老师的模板和教导,感谢ztdl,jldl。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号