卷积是CNN非常核心的操作,CNN主要就是通过卷积来实现特征提取的,在卷积操作的计算中会设计到几个概念:步长(strides)、补充(padding)、卷积核(kernel)等,那卷积的输出分辨率计算一般就会与这几个参数有关(空洞或者扩张卷积暂时不纳入这个范围),以下计算不做说明的话,均考虑卷积核大小为3*3。所以这一篇就以二维卷积为例子简单记录下卷积的一点计算公式。
以下以s代表步长,p代表补充,k代表卷积核、i代表输入分辨率、o代表输出分辨率,[]代表向下取整(因为公式编辑器里找不到向下取整的符号,以此代替):
一、padding=0、strides=1

这一种比较简单,输出为输入减去卷积核加1:
![]()
二、padding=half(same)、strides=1

这种情况是指补充的大小为卷积核一半,即:
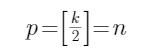
输出的计算为:
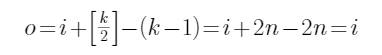
也就是说,此时的输出是等于输入尺寸的。
三、padding=full

这种情况是指padding的大小等于k-1,步长为1:
![]()
四、padding=0,strides!=1
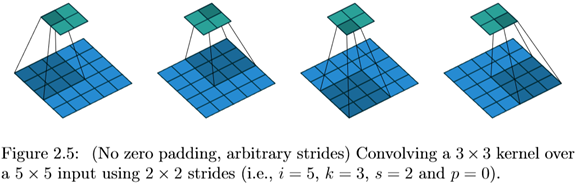
这种情况下,不做补充,但是步长是任意取的,计算公式如下:
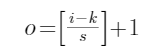
五、padding!=0,strides!=1

输出为:

参考
[1] Dumoulin V, Visin F. A guide to convolution arithmetic for deep learning[J]. 2016.
你不愿意种花
你说:
“我不愿看见它一点点凋落”
是的
为了避免结束
您避免了一切开始
-- 顾城
上善若水,为而不争。


