上一篇介绍了卷积的输出分辨率计算，现在这一篇就来写下转置卷积的分辨率计算。转置卷积(Transposed convolution),转置卷积也有叫反卷积(deconvolution)或者fractionally strided convolutions。

根据《A guide to convolution arithmetic for deep learning》的介绍的话，在进行卷积操作的时候我们是可以把卷积操作重写为以下的形式：

这个时候，输出是可以表示为

 

如果反向操作，输入为y的话，要得到x的话，其实就只要一个C的转置去乘以y就可以得到一个分辨率与x一样的输出：

而这个CT也是由输入的卷积核重构出来的。

接下来就分类计算转置卷积的输出分辨率：

一、padding!=0，strides=1

不做padding，步长为1的情况下，输出计算是比较简单的：

 

二、padding=half(same)，strides=1

此时的输出分辨率是等于输入分辨率的。

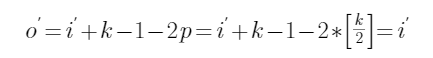
其中，[]代表向下取整，

三、padding=full,strides=1

 

此时的p=k-1，所以输出分辨率为：

 

四、padding=0，strides!=1

 

 

五、padding!=0,strides!=1

输出分辨率为：

 

此时输出表示为：

其中，表示添加到右边和下边的0的个数。

参考

[1] Dumoulin V, Visin F. A guide to convolution arithmetic for deep learning[J]. 2016

过完了这个月，我们打开门

一些花开在高高的树上

一些果结在深深的地下

  -- 海子 《新娘》