【Foreign】登山 [DP][数学]

登山

Time Limit: 10 Sec  Memory Limit: 256 MB

Description

　　恶梦是一个登山爱好者，今天他来到了黄山
　　俗话说的好，不走回头路。所以在黄山，你只能往前走，或者往上走。
　　并且很显然的是，当你走到山脊的时候，你不能够往上走，你只能往前走一步再往上走。
　　抽象一点而言就是，你可以把黄山视为一个N * N格点图，恶梦从(0,0)开始出发，要走到 (N,N)。
　　当他走到位置(x,y)的时候，它可以往(x + 1,y),或(x,y+1)走。
　　并且当他走到(x,x)的时候，由于他已经处在了山脊上，所以他不能够往(x,x+1)方向上走。
　　当恶梦兴致勃勃准备开始爬山的时候，他的同伴告诉他，黄山由于年久失修，有一些位置出现了大坑，不能走。
　　恶梦觉得更刺激了，但他想先知道他能有多少种方式走到黄山顶。
　　由于这个数字很大，所以你只需要将答案对10^9 + 7取模输出即可。

Input

　　第一行包括两个整数N,C,分别表示你可以把黄山视作一个N * N的格点图，并且黄山上面有C个位置出现了大坑。
　　接下来的C行，每行包括两个整数X,Y,表示X,Y这个位置不能走。
　　保证X>=Y,也就是说(X,Y)必然在山上。
　　保证这C个点互不相同。

Output

　　输出只有一个整数Ans,表示恶梦爬上山顶的路径数对10^9+7取模的值。

Sample Input

　　5 2
　　5 0
　　1 1

Sample Output

　　27

HINT

　　对于100%的数据，保证N<=100000,C<=1000。
　　保证对于(0,0),(N,N)不存在障碍点。

Solution

　　这显然是一道数学题，结合DP，我们令 f[i] 表示不经过其它障碍点，首先经过障碍点 i 的方案数。

　　那么显然有：f[i] = Ways(0,0 -> i) - f[j] * Ways(i -> j)。

　　问题就转化为了，怎样求出满足不超过直线y=x+1，从一点走向另外一点的方案数。

 

　　

　　

　　

 

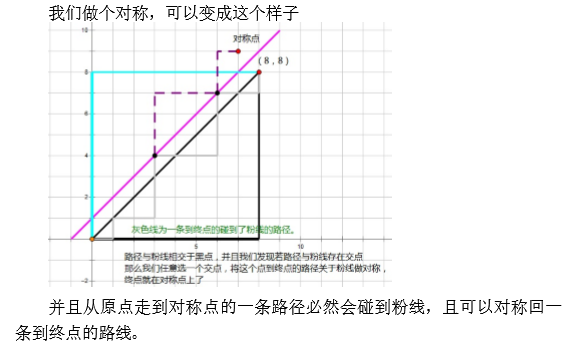
　　所以Ways = ((x1, y1) -> (x2, y2)) - ((x1, y1) -> (y2-1, x2+1))。

　　统计答案只要加入一个(n, n)在f里面计算即可。

Code

#include<iostream>
#include<string>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
using namespace std;
typedef long long s64;

const int ONE = 5000005;
const int MOD = 1e9 + 7;

int n, m;
int x, y;
int fac[ONE], inv[ONE];
int f[ONE];

struct point
{
        int x, y;
}a[ONE];
bool cmp(const point &a, const point &b)
{
        if(a.x != b.x) return a.x < b.x;
        return a.y < b.y;
}

int get()
{
        int res=1,Q=1;  char c;
        while( (c=getchar())<48 || c>57)
        if(c=='-')Q=-1;
        if(Q) res=c-48; 
        while((c=getchar())>=48 && c<=57) 
        res=res*10+c-48;
        return res*Q; 
}

int Quickpow(int a, int b)
{
        int res = 1;
        while(b)
        {
            if(b & 1) res = (s64)res * a % MOD;
            a = (s64)a * a % MOD;
            b >>= 1;
        }
        return res;
}

void Deal_first()
{
        fac[0] = 1;
        for(int i = 1; i <= 2 * n; i++)
            fac[i] = (s64)fac[i - 1] * i % MOD;
        inv[2 * n] = Quickpow(fac[2 * n], MOD - 2);
        for(int i = 2 * n - 1; i >= 0; i--)
            inv[i] = (s64)inv[i + 1] * (i + 1) % MOD;
}

int C(int n, int m)
{
        if(n < 0 || m < 0) return 0;
        return (s64)fac[n] * inv[m] % MOD * inv[n - m] % MOD;
}

void Modit(int &a)
{
        if(a < 0) a += MOD;
        if(a >= MOD) a -= MOD;
}

int Ways(point a, point b)
{
        if(n < 0 || m < 0) return 0;
        return C(b.y - a.y + b.x - a.x, b.y - a.y);
}

int Getit(point a, point b)
{
        return Ways(a, b) - Ways(a, (point){b.y - 1, b.x + 1});
}

int main()
{
        n = get();    m = get();
        Deal_first();

        for(int i = 1; i <= m; i++)
            a[i].x = get(), a[i].y = get();

        a[++m] = (point){n, n};
        sort(a + 1, a + m + 1, cmp);

        for(int i = 1; i <= m; i++)
        {
            Modit(f[i] = Getit((point){0, 0}, a[i]));
            for(int j = 1; j < i; j++)
                Modit(f[i] -= (s64)f[j] * Getit(a[j], a[i]) % MOD);
        }

        printf("%d", f[m]);
}