【Codeforces549F】Yura and Developers [单调栈][二分]
Yura and Developers
Time Limit: 20 Sec Memory Limit: 512 MBDescription

Input

Output
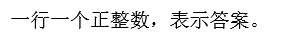
Sample Input
4 3
5 2 4 4
5 2 4 4
Sample Output
2
HINT
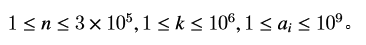
Solution
首先,我们先用单调栈求出以点 i 作为最大值的区间 [pre_i, suc_i]。然后显然就是 求 [pre_i, suc_i] 内有几个区间的和与val[i] %k同余。
我们记区间为 [L, mid, R](i 为mid,pre_i 为 L,suc_i 为R),显然我们可以枚举长度小的半个区间。这时效率是O(nlogn)的。
那么只要能求出另外一半的贡献即可,假定我们枚举 [L, mid - 1] 的一个 点begin。那么 [begin, mid - 1] 的和是固定的,我们又知道总和应该为多少(%k同余)。所以我们就可以知道剩下需要提供多少值。 问题就转化为了求:[mid, mid ~ R] 中有几个以 mid 为左端点,mid~R为右端点的区间 的和 %k余 一个定值。
我们考虑这个东西怎么求,显然可以将问题转化为查前缀和形式:
我们已知 [1, mid - 1] 的和%k的值,又由于[mid, mid~R] 要提供一个定值的贡献,所以可以算出 [1, mid~R] 要余多少。
那么我们就可以通过查前缀和解决这个子问题,现在的问题又转化为了 如何查询一个区间 [L, R] 内某一定值数的个数:
显然我们可以 把位置加入在一个以值为下标的vector中,在这个vector中,二分查询位置<=R的个数即可,减去 <=(L - 1) 的即可。
这样我们就解决了假定[L, mid - 1]固定的一部分,假定[mid + 1, R]固定同理。
我们就解决了这道题啦!QWQ
Code

1 #include<iostream> 2 #include<string> 3 #include<algorithm> 4 #include<cstdio> 5 #include<cstring> 6 #include<cstdlib> 7 #include<cmath> 8 #include<vector> 9 using namespace std; 10 typedef long long s64; 11 12 const int ONE = 1000005; 13 const int MOD = 1e9 + 7; 14 15 int n, k; 16 s64 val[ONE]; 17 int pre[ONE], suc[ONE]; 18 s64 sum[ONE], sum_B[ONE]; 19 s64 Ans; 20 21 vector <int> A[ONE], B[ONE]; 22 23 int get() 24 { 25 int res;char c; 26 while( (c=getchar())<48 || c>57 ); 27 res=c-48; 28 while( (c=getchar())>=48 && c<=57 ) 29 res=res*10+c-48; 30 return res; 31 } 32 33 void Deal_first() 34 { 35 int stk[ONE], top = 0; 36 for(int i = 1; i <= n; i++) 37 { 38 while(top && val[i] > val[stk[top]]) 39 suc[stk[top--]] = i - 1; 40 pre[i] = stk[top] + 1; 41 stk[++top] = i; 42 } 43 while(top) suc[stk[top--]] = n; 44 45 for(int i = 1; i <= n; i++) 46 sum[i] = (sum[i - 1] + val[i]) % k; 47 for(int i = n; i >= 1; i--) 48 sum_B[i] = (sum_B[i + 1] + val[i]) % k; 49 50 for(int i = 1; i <= n; i++) 51 { 52 A[sum[i]].push_back(i); 53 B[sum_B[i]].push_back(i); 54 } 55 } 56 57 int Get(int l, int r) 58 { 59 int res = sum[r] - sum[l - 1]; 60 if(res < 0) res += k; 61 return res; 62 } 63 int Find(int R, int val) 64 { 65 if(A[val].size() == 0) return 0; 66 int l = 0, r = A[val].size() - 1; 67 while(l < r - 1) 68 { 69 int mid = l + r >> 1; 70 if(A[val][mid] > R) r = mid; 71 else l = mid; 72 } 73 if(A[val][l] > R) return l; 74 if(A[val][r] > R) return r; 75 return A[val].size(); 76 } 77 int Query_left(int L, int R, int val) //sum [L,L~R] num of val 78 { 79 if(L > R) return 0; 80 int now = sum[L - 1]; //[1, L - 1] 81 int need = (now + val) % k; //1 ~ R the num of presum = need 82 return Find(R, need) - Find(L - 1, need); 83 } 84 void Deal_left(int l, int mid, int r) 85 { 86 int T = val[mid] % k; 87 for(int i = l; i <= mid - 1; i++) 88 { 89 int now = Get(i, mid - 1); 90 int need = (T - now + k) % k; 91 Ans += Query_left(mid, r, need); 92 } 93 94 Ans += Query_left(mid, r, T) - 1; 95 } 96 97 98 int Get_B(int l, int r) 99 { 100 int res = sum_B[l] - sum_B[r + 1]; 101 if(res < 0) res += k; 102 return res; 103 } 104 int Find_B(int R, int val) 105 { 106 if(B[val].size() == 0) return 0; 107 int l = 0, r = B[val].size() - 1; 108 while(l < r - 1) 109 { 110 int mid = l + r >> 1; 111 if(B[val][mid] > R) r = mid; 112 else l = mid; 113 } 114 if(B[val][l] > R) return l; 115 if(B[val][r] > R) return r; 116 return B[val].size(); 117 } 118 int Query_right(int L, int R, int val) 119 { 120 if(L > R) return 0; 121 int now = sum_B[R + 1]; 122 int need = (now + val) % k; 123 return Find_B(R, need) - Find_B(L - 1, need); 124 } 125 void Deal_right(int l, int mid, int r) 126 { 127 int T = val[mid] % k; 128 for(int i = mid + 1; i <= r; i++) 129 { 130 int now = Get_B(mid + 1, i); 131 int need = (T - now + k) % k; 132 Ans += Query_right(l, mid, need); 133 } 134 Ans += Query_right(l, mid, T) - 1; 135 } 136 137 int main() 138 { 139 n = get(); k = get(); 140 for(int i = 1; i <= n; i++) 141 val[i] = get(); 142 143 Deal_first(); 144 145 for(int i = 1; i <= n; i++) 146 { 147 if(i - pre[i] + 1 <= suc[i] - i + 1) 148 Deal_left(pre[i], i, suc[i]); 149 else 150 Deal_right(pre[i], i, suc[i]); 151 } 152 153 printf("%lld", Ans); 154 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号