【Codeforces629C】Famil Door and Brackets [DP]

Famil Door and Brackets

Time Limit: 20 Sec  Memory Limit: 512 MB

Description

　　

Input

　　

Output

　　

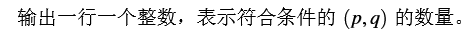
Sample Input

　　4 1
　　(

Sample Output

　　4

HINT

　　

Solution

　　显然，我们考虑运用DP。先求出 f[i][j] 表示 长度为 i 的括号序列，“)” 比 “(” 多 j 个的方案（时刻保证 j >= 0）。

　　然后我们考虑怎样获得答案。先预处理出L，R表示将读入的括号序列消去若干对之后剩下的“)” “(”个数（消去吼显然形如“))(((”）。

　　那么我们左边要加入的就要至少多R个“(”，右边类似。

　　但是显然，我也可以左边再多填几个“(”，右边再多填几个“)”。

　　那么我们就可以 枚举左边填 i 个括号（则右边填 need - i 个），左边多填 num 个“(”（则右边多填 num 个“)”）。

　　然后统计答案即可。

Code

#include<iostream>  
#include<string>  
#include<algorithm>  
#include<cstdio>  
#include<cstring>  
#include<cstdlib>  
#include<cmath>
using namespace std;
typedef long long s64;
 
const int ONE = 800005;
const int MOD = 1e9 + 7;
const int Base = 2005;

int n, m, need;
char s[ONE];
int f[2005][2005];
int Ans;
int stk[ONE], top;
int L = 0, R = 0;

int get() 
{ 
        int res;char c; 
        while( (c=getchar())<48 || c>57 );
        res=c-48;  
        while( (c=getchar())>=48 && c<=57 ) 
        res=res*10+c-48; 
        return res; 
} 

void Deal_f()
{
        f[0][0] = 1;
        for(int i = 1; i <= need; i++)
            for(int j = 0; j <= need; j++)
            {
                f[i][j] = (f[i][j] + f[i - 1][j + 1]) % MOD;
                if(j >= 1) f[i][j] = (f[i][j] + f[i - 1][j - 1]) % MOD;
            }
}

void Deal_LR()
{
        for(int i = 1; i <= m; i++)
        {
            if(s[i] == ')' && stk[top] == '(') top--;
            else stk[++top] = s[i]; 
        }

        for(int i = 1; i <= top; i++)
            if(stk[i] == '(') L++;
            else R++;
}

int main()
{
        n = get();    m = get();    need = n - m;
        scanf("%s", s + 1);

        Deal_f(), Deal_LR();

        Ans = 0;
        for(int i = 0; i <= need; i++)
            for(int num = 0; num <= need; num++)//left's L
                if(R + num < 2005 && L + num < 2005)
                       Ans = (Ans + (s64)f[i][R + num] * f[need - i][L + num] % MOD) % MOD;

        printf("%d", Ans);
}

 

 

• 视图代码