【BZOJ1043】下落的圆盘 [计算几何]

下落的圆盘

Time Limit: 10 Sec  Memory Limit: 162 MB
[Submit][Status][Discuss]

Description

　　有n个圆盘从天而降，后面落下的可以盖住前面的。求最后形成的封闭区域的周长。

　　看下面这副图, 所有的红色线条的总长度即为所求。

　　

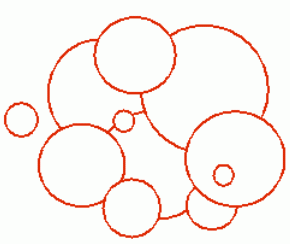
Input

　　第一行为1个整数n
　　接下来n行每行3个实数,ri,xi,yi,表示下落时第i个圆盘的半径和圆心坐标.

Output

　　最后的周长，保留三位小数

Sample Input

　　2
　　1 0 0
　　1 1 0

Sample Output

　　10.472

HINT

　　n <= 1000

Solution

　　显然是一道计算几何题。

　　考虑一个圆对于答案的贡献，显然是这个圆的周长 - 后面的圆把它覆盖掉的周长的并。那么我们就考虑怎么求这个并。

　　先考虑怎样记录下一个答案，显然直接扣掉单个圆对它的覆盖是不可行的，要减去重叠的情况。

　　既然边不可行，我们就用角度。显然，若我们求出 两圆交点的角度 即可解决这题。

　　我们考虑求圆A被圆B覆盖的角度：现在我们有两个圆的半径、圆心距。我们就可以得到 圆A与圆B的圆心连线 与 圆A半径 的夹角。

　　我们也可以知道 圆A与圆B的圆心连线 与 x轴的夹角。

　　这样的话，就可以把单个圆对于它的贡献记录到栈里面，最后扫一遍求一下剩余的角度，乘上R就是它对于答案的贡献了。

Code

 

#include<iostream>    
#include<string>    
#include<algorithm>    
#include<cstdio>    
#include<cstring>    
#include<cstdlib>
#include<cmath>
#include<queue>
using namespace std;  
typedef unsigned long long s64;

const int ONE = 1000005;
const double pi = acos(-1.0);

int n;
struct power
{
        double x, y, r;
}a[ONE];

struct circle
{
        double a, b;
}stk[ONE];
int top;

double Ans;

bool cmp(const circle &a, const circle &b)
{
        if(a.a != b.a) return a.a < b.a;
        return a.b < b.b;
}

int get()
{ 
        int res,Q=1;    char c;
        while( (c=getchar())<48 || c>57)
        if(c=='-')Q=-1;
        if(Q) res=c-48; 
        while((c=getchar())>=48 && c<=57) 
        res=res*10+c-48; 
        return res*Q; 
}

double sqr(double x) {return x * x;}
double dist(power a, power b) {return sqrt(sqr(a.x - b.x) + sqr(a.y - b.y));}

double Calc(power a, power b)
{
        double A = a.r, B = b.r, C = dist(a, b);
        double cosB = (sqr(A) + sqr(C) - sqr(B)) / (2 * A * C);
        double angle = atan2(a.x - b.x, a.y - b.y), add = acos(cosB);
        stk[++top] = (circle){angle - add, angle + add};
}

double init(power a, power b) {return a.r + dist(a, b) <= b.r;}
double sect(power a, power b) {return fabs(a.r - b.r) < dist(a, b) && dist(a, b) < a.r + b.r;}

double Deal(int id)
{
        top = 0;
        for(int i = id+1; i <= n; i++)
            if(init(a[id], a[i])) return 0;
        
        for(int i = id+1; i <= n; i++)
            if(sect(a[id], a[i])) Calc(a[id], a[i]);
        
        for(int i = 1; i <= top; i++)
        {
            while(stk[i].a < 0) stk[i].a += 2 * pi;
            while(stk[i].b < 0) stk[i].b += 2 * pi;
            if(stk[i].a > stk[i].b) stk[++top] = (circle){0, stk[i].b}, stk[i].b = 2*pi;
        }
        
        sort(stk + 1, stk + top + 1, cmp);
        double last = 0.0, sum = 0.0;
        for(int i = 1; i <= top; i++)
            if(stk[i].a > last) sum += stk[i].a - last, last = stk[i].b;
            else last = max(last, stk[i].b);
        
        sum += 2 * pi - last;
        return a[id].r * sum;
}

int main()
{
        n = get();
        for(int i = 1; i <= n; i++)
            scanf("%lf %lf %lf", &a[i].r, &a[i].x, &a[i].y);
        for(int i = 1; i <= n; i++)
            Ans += Deal(i);
        printf("%.3lf", Ans);
}