【BZOJ2818】Gcd [莫比乌斯反演]

Gcd

Time Limit: 10 Sec  Memory Limit: 256 MB
[Submit][Status][Discuss]

Description

　　给定整数N，求1<=x,y<=N且Gcd(x,y)为素数的
　　数对(x,y)有多少对.

Input

　　一个整数N

Output

　　如题

Sample Input

　　4

Sample Output

　　4

HINT

　　1<=N<=10^7

Solution

　　直接莫比乌斯反演即可。

　　

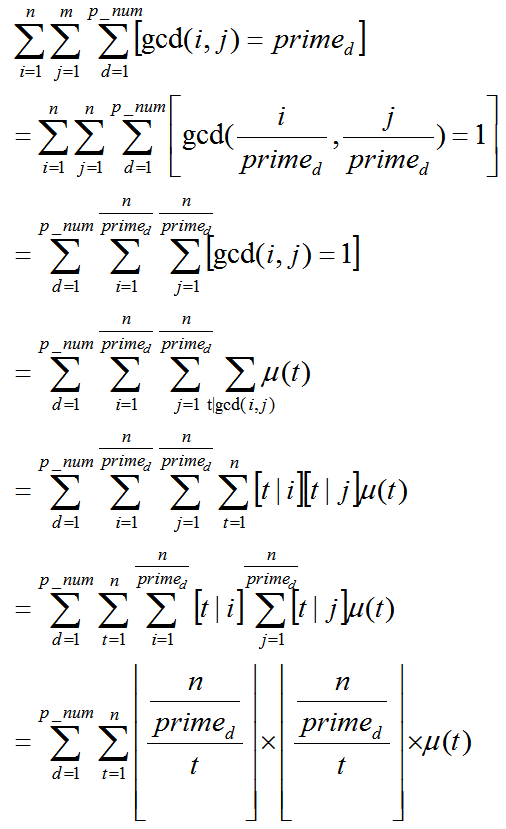
　　然后对于这个式子，我们下界分块一下即可。

Code

 1 #include<iostream>  
 2 #include<string>  
 3 #include<algorithm>  
 4 #include<cstdio>  
 5 #include<cstring>  
 6 #include<cstdlib>  
 7 #include<cmath>
 8 using namespace std; 
 9 typedef long long s64;
10   
11 const int ONE = 1e7+5;
12     
13 int T;
14 int n,m;
15 bool isp[ONE];
16 int prime[664580],p_num;
17 int miu[ONE],sum_miu[ONE];
18 s64 Ans;
19  
20 int get() 
21 {
22         int res=1,Q=1;  char c;
23         while( (c=getchar())<48 || c>57)
24         if(c=='-')Q=-1;
25         if(Q) res=c-48; 
26         while((c=getchar())>=48 && c<=57) 
27         res=res*10+c-48; 
28         return res*Q; 
29 }
30   
31 void Getmiu(int MaxN)
32 {
33         miu[1] = 1;
34         for(int i=2; i<=MaxN; i++)
35         {
36             if(!isp[i])
37                 isp[i] = 1, prime[++p_num] = i, miu[i] = -1;
38             for(int j=1; j<=p_num, i*prime[j]<=MaxN; j++)
39             {
40                 isp[i * prime[j]] = 1;
41                 if(i % prime[j] == 0)
42                 {
43                     miu[i * prime[j]] = 0;
44                     break;
45                 }
46                 miu[i * prime[j]] = -miu[i];
47             }
48             miu[i] += miu[i-1];
49         }
50 }
51   
52 int main()
53 {
54         n=get();
55         Getmiu(n);
56         for(int d=1; d<=p_num; d++)
57         {
58             if(prime[d] > n) break;
59             int N = n/prime[d];
60             for(int i=1,j=0; i<=N; i=j+1)
61             {
62                 j = min(N, N/(N/i));
63                 Ans += (s64)(N/i) * (N/i) * (miu[j] - miu[i-1]);
64             }
65         }
66          
67         printf("%lld",Ans);
68 }
View Code

 

posted @ 2017-04-02 15:58  BearChild  阅读(167)  评论(0)  编辑  收藏  举报