【Foreign】魔法 [组合数][质因数分解]
魔法
Time Limit: 10 Sec Memory Limit: 256 MBDescription
Input
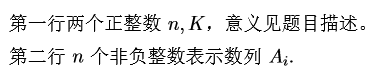
Output
仅一行一个整数表示答案。
Sample Input
4 10
7 2 8 5
7 2 8 5
Sample Output
2
HINT
Solution
我们找一下规律，显然发现是就是Σa[i]*C(n-1,i-1)。然后问题主要就转化为了怎么快速求组合数C(n,i)在模一个非质数情况下的值。
首先我们先确定一个式子：
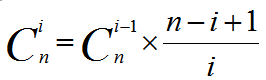
然后我们立马想到了一个暴力分解质因数的方法。就是记录所有的(n-i+1)和(i)的质因数，然后用上面的质因数个数减去下面的质因数个数，剩下的乘起来，就不用求取模了。
但是我们发现，这样显然会TLE，我们考虑如何优化。优化的话显然就是要找到一个办法不把多的质因数都彻底分解出来。我们来继续思考：
我们可以先求出模数的质因数，再对于(n-i+1)和(i)分解质因数。这时候如果质因数和模数的质因数一样，由于不互质没有逆元，就把它记录下来，等下用快速幂乘起来就行了。那么这时候其余的质因数就可以直接求逆元了，由于模数不是质数，我们运用这个公式：（phi暴力求即可）
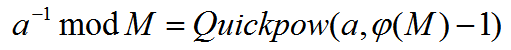
这样做的话，由于模数的质因数是个数有限的，拆解其余数可以减少很多部分，那么效率就可以得到保证啦。
Code
1 #include<iostream>
2 #include<algorithm>
3 #include<cstdio>
4 #include<cstring>
5 #include<cstdlib>
6 #include<cmath>
7 using namespace std;
8 typedef long long s64;
9
10 const int Max = 1000005;
11 const int ONE = 1000005;
12
13 int n,x,MOD;
14 int a[ONE];
15 int f[Max],p[Max],p_num;
16 int Num[Max];
17 int Ans;
18
19 int get()
20 {
21 int res=1,Q=1; char c;
22 while( (c=getchar())<48 || c>57)
23 if(c=='-')Q=-1;
24 if(Q) res=c-48;
25 while((c=getchar())>=48 && c<=57)
26 res=res*10+c-48;
27 return res*Q;
28 }
29
30 int Quickpow(int a,int b)
31 {
32 int res=1;
33 while(b)
34 {
35 if(b&1) res=(s64)res*a%MOD;
36 a=(s64)a*a%MOD;
37 b>>=1;
38 }
39 return res;
40 }
41
42 void Deal_prime(int x)
43 {
44 for(int i=2;i*i<=x;i++)
45 if(!(x%i))
46 {
47 p[++p_num]=i;
48 while(!(x%i)) x/=i;
49 }
50 if(x>1) p[++p_num]=x;
51 }
52
53 int gcd(int a,int b) {int r=a%b; while(r) {a=b;b=r;r=a%b;} return b;}
54 int phi(int x) {int res=0; for(int i=1;i<x;i++)if(gcd(i,x)==1) res++;return res;}
55
56 int Add(int x,int P)
57 {
58 if(!x || x==1) return x;
59 for(int i=1;i<=p_num;i++)
60 {
61 while(!(x%p[i]))
62 {
63 x/=p[i];
64 Num[p[i]]+=P;
65 }
66 if(x==1) break;
67 }
68 return x;
69 }
70
71 int main()
72 {
73 n=get(); MOD=get();
74 Deal_prime(MOD);
75 int Phi = phi(MOD);
76
77 int C=1;
78 int record=1;
79 for(int i=1;i<=n;i++)
80 {
81 x=get();
82 Ans = (Ans+ (s64)record * x % MOD) % MOD;
83 if(i==n) break;
84 C = (s64)C * Add(n-i,1) % MOD * Quickpow(Add(i,-1),Phi-1) % MOD;
85 record=C;
86 for(int j=1;j<=p_num;j++)
87 record= (s64)record * Quickpow(p[j],Num[p[j]]) % MOD;
88 }
89
90 printf("%d",Ans);
91 }
