【BZOJ4657】tower [网络流]
炮塔
Time Limit: 10 Sec Memory Limit: 256 MBDescription
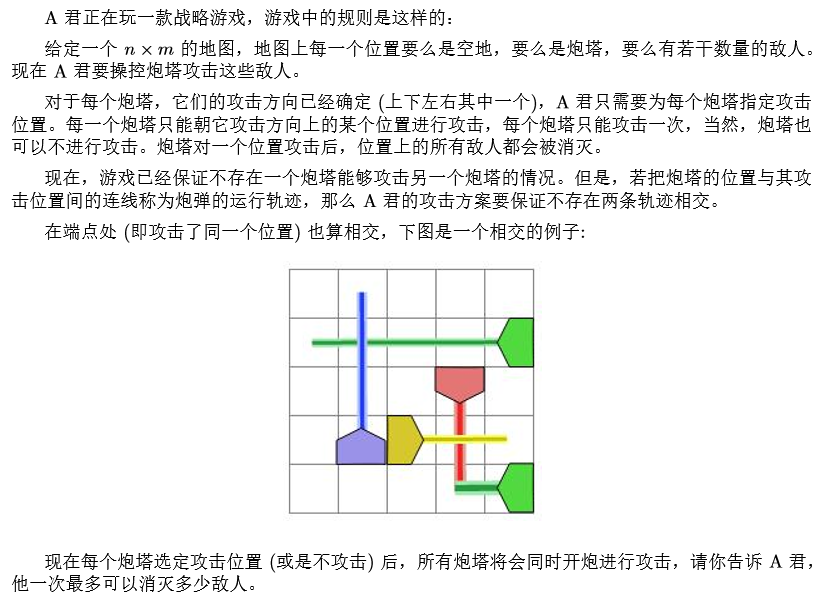
Input
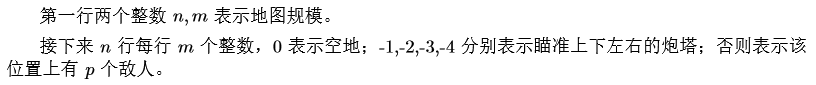
Output
一行一个整数表示答案。
Sample Input
4 5
0 0 -2 0 0
-4 0 5 4 0
0 -4 3 0 6
9 0 0 -1 0
0 0 -2 0 0
-4 0 5 4 0
0 -4 3 0 6
9 0 0 -1 0
Sample Output
12
HINT

Main idea
给定若干固定方向的炮台,以及若干位置的敌人,炮台可以杀掉对应方向上从该位置到底的其中一个位置的敌人,要求炮台位置和消灭的敌人位置连线,连线不能有重叠,询问最多能消灭几个敌人。
Solution
我们发现,相交的连线其实就是给出了炮台之间的路径。我们来处理如何解决无可走路径的问题,显然想到了最小割。
横向炮台或纵向炮台之间是没有影响的。所以显然可以构建一张二分图。
那么我们如何确定容量呢?我们可以令一条 (u->v) 的割边表示选择了u这个点。方便处理连边上下或左右攻击的炮台,连边方向应该一致。然后我们连边时先找到一条可攻击位置上的最大贡献,设最大贡献为Max,然后连边时容量用Max-val,就表示它会损失这么多的价值。注意到这样连边的话,在最边界上的点是没有连边的。但是并不会影响答案,为什么呢?我们这么考虑:如果我们选择了最边界的点,那么这个位置的敌人数必然是最多的,如果不是最多的话(也就是说还有其它点人数更多)显然连到边界不可能是最优的,因为连边界就可能阻断了更多其它炮台攻击方案的可能性。这就表示了,若选择边界,则必然边界贡献最多,那么如果连边了,容量也应该是0,综上所述不会影响答案。
我们这样连完了边,但发现还是会有一些问题。如果出现这种情况,就会有一些Bug:
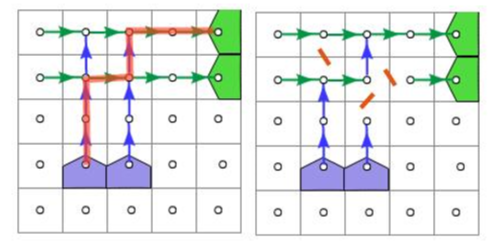
这样就会影响了答案。怎么处理呢?我们发现问题只能涉及一行一列,只要令路径只能“拐一次弯”就可以解决。所以我们可以再将点拆为横向点和纵向点,横向点向纵向点连INF的边,纵向点没有边连向横向点即可。
这样的话复杂度就是O(maxflow(n×m,n×m)),成功了解决了问题!\(≧▽≦)/
Code

1 #include<iostream>
2 #include<algorithm>
3 #include<cstdio>
4 #include<cstring>
5 #include<cstdlib>
6 #include<cmath>
7 using namespace std;
8
9 const int ONE = 100001;
10 const int INF = 214783640;
11
12 int n,m;
13 int S,T;
14 int Ans;
15 int a[101][101],Max;
16 int next[ONE],first[ONE],go[ONE],w[ONE],tot;
17 int q[10000001],Dep[ONE],E[ONE],tou,wei;
18 #define id(i,j) (i-1)*m+j
19
20 int get()
21 {
22 int res,Q=1; char c;
23 while( (c=getchar())<48 || c>57)
24 if(c=='-')Q=-1;
25 if(Q) res=c-48;
26 while((c=getchar())>=48 && c<=57)
27 res=res*10+c-48;
28 return res*Q;
29 }
30
31 void Add(int u,int v,int z)
32 {
33 next[++tot]=first[u]; first[u]=tot; go[tot]=v; w[tot]=z;
34 next[++tot]=first[v]; first[v]=tot; go[tot]=u; w[tot]=0;
35 }
36
37 int Bfs()
38 {
39 memset(Dep,0,sizeof(Dep));
40 tou=0; wei=1;
41 q[1]=S; Dep[S]=1;
42 for(int u=S;u<=T;u++) E[u]=first[u];
43 while(tou < wei)
44 {
45 int u=q[++tou];
46 for(int e=first[u];e;e=next[e])
47 {
48 int v=go[e];
49 if(Dep[v] || !w[e]) continue;
50 Dep[v] = Dep[u] + 1;
51 q[++wei] = v;
52 }
53 }
54 return Dep[T] > 0;
55 }
56
57 int Dfs(int u,int Limit)
58 {
59 if(u==T || !Limit) return Limit;
60 int flow=0,f;
61 for(int &e=E[u]; e; e=next[e])
62 {
63 int v=go[e];
64 if(Dep[v]!=Dep[u]+1 || !w[e]) continue;
65 f=Dfs(v,min(w[e],Limit));
66 w[e] -= f;
67 w[((e-1)^1)+1] += f;
68 Limit -= f;
69 flow += f;
70 if (!Limit) break;
71 }
72 return flow;
73 }
74
75 int main()
76 {
77 n=get(); m=get();
78 for(int i=1;i<=n;i++)
79 for(int j=1;j<=m;j++)
80 {
81 a[i][j] = get();
82 }
83
84 int PD=n*m;
85 S=0; T=2*PD+1;
86 for(int i=1;i<=n;i++)
87 for(int j=1;j<=m;j++)
88 {
89 if(a[i][j] == -1)
90 {
91 Max = a[i][j] = 0;
92 Add(S,id(i,j),INF);
93 for(int k=i-1;k>=1;k--) Max = max(Max, a[k][j]);
94 for(int k=i;k>=1+1;k--) Add(id(k,j), id(k-1,j), Max-a[k][j]);
95 Ans += Max;
96 }
97
98 else
99 if(a[i][j] == -2)
100 {
101 Max = a[i][j] = 0;
102 Add(S,id(i,j),INF);
103 for(int k=i+1;k<=n;k++) Max = max(Max, a[k][j]);
104 for(int k=i;k<=n-1;k++) Add(id(k,j), id(k+1,j), Max-a[k][j]);
105 Ans += Max;
106 }
107
108 else
109 if(a[i][j] == -3)
110 {
111 Max = a[i][j] = 0;
112 Add(id(i,j)+PD,T,INF);
113 for(int k=j-1;k>=1;k--) Max = max(Max, a[i][k]);
114 for(int k=j;k>=1+1;k--) Add(id(i,k-1)+PD, id(i,k)+PD, Max-a[i][k]);
115 Ans += Max;
116 }
117
118 else
119 if(a[i][j] == -4)
120 {
121 Max = a[i][j] = 0;
122 Add(id(i,j)+PD,T,INF);
123 for(int k=j+1;k<=m;k++) Max = max(Max, a[i][k]);
124 for(int k=j;k<=m-1;k++) Add(id(i,k+1)+PD, id(i,k)+PD, Max-a[i][k]);
125 Ans += Max;
126 }
127
128 else
129 {
130 Add(id(i,j), id(i,j)+PD, INF);
131 }
132 }
133
134 while(Bfs()) Ans-=Dfs(S,INF);
135
136 printf("%d",Ans);
137 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号