【BZOJ2815】【ZJOI2012】灾难 [LCA]
灾难
Time Limit: 10 Sec Memory Limit: 128 MB[Submit][Status][Discuss]
Description
阿米巴是小强的好朋友。
阿米巴和小强在草原上捉蚂蚱。小强突然想,如果蚂蚱被他们捉灭绝了,那么吃蚂蚱的小鸟就会饿死,而捕食小鸟的猛禽也会跟着灭绝,从而引发一系列的生态灾难。
学过生物的阿米巴告诉小强,草原是一个极其稳定的生态系统。如果蚂蚱灭绝了,小鸟照样可以吃别的虫子,所以一个物种的灭绝并不一定会引发重大的灾难。
我们现在从专业一点的角度来看这个问题。我们用一种叫做食物网的有向图来描述生物之间的关系:
一个食物网有 N个点,代表 N 种生物,如果生物 x 可以吃生物 y,那么从 y 向 x 连一个有向边。
这个图没有环。
图中有一些点没有连出边,这些点代表的生物都是生产者,可以通过光合作用来生存; 而有连出边的点代表的都是消费者,它们必须通过吃其他生物来生存。
如果某个消费者的所有食物都灭绝了,它会跟着灭绝。
我们定义一个生物在食物网中的“灾难值”为,如果它突然灭绝,那么会跟着一起灭绝的生物的种数。
举个例子:在一个草场上,生物之间的关系是:
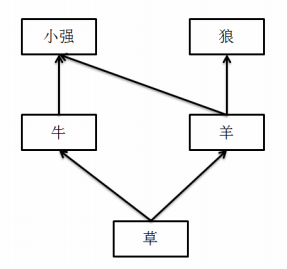
如果小强和阿米巴把草原上所有的羊都给吓死了,那么狼会因为没有食物而灭绝,而小强和阿米巴可以通过吃牛、牛可以通过吃草来生存下去。所以,羊的灾难值是 1。但是,如果草突然灭绝,那么整个草原上的 5 种生物都无法幸免,所以草的灾难值是4,请求出所有的灾难值。
Input
第一行是一个正整数 N,表示生物的种数。生物从 1 标号到 N。
接下来 N 行,每行描述了一个生物可以吃的其他生物的列表,格式为用空格隔开的若干个数字,每个数字表示一种生物的标号,最后一个数字是 0 表示列表的结束。
Output
包含N行,每行一个整数,表示每个生物的灾难值。
Sample Input
5
0
1 0
1 0
2 3 0
2 0
Sample Output
4
1
0
0
0
HINT
对 100%的数据,1 ≤ N ≤ 65534。
输入文件的大小不超过 1M。保证输入的食物网没有环。
Main idea
每个点删去后可以影响到一个点,一个点被删去的条件是所有指向它的点都被删去,求一个点被删去后可以直接影响到几个点。
Solution
首先知道一个点至多有一个点使得那个点删除后直接影响到该点的,所以可以想到树形结构,也就是建立一棵“灭绝树”。
我们定义“灭绝树”满足以下性质:对于一棵多叉树的任意一个结点,当它“灭绝”时,它所有的后代也会跟着“灭绝”。
如何建立呢?首先利用拓扑序顺序进行操作,因为在前面的点可以影响到后面的点,而做到后面的点的时候前面的点已经处理完毕了,然后利用图的反向图,该点在灭绝树中的父亲是在反向图中所有儿子的LCA,因为只有LCA灭绝了才可以导致该点直接灭绝,那么最后答案显然就是一个点在灭绝树中的子树大小,由于可能有多个根节点,所以我们假设一个超级点为0,如果一个点入度为0则连向0,由0跑DFS求size(子树个数),最后size要-1。
Code

1 #include<iostream>
2 #include<algorithm>
3 #include<cstdio>
4 #include<cstring>
5 #include<cstdlib>
6 #include<cmath>
7 using namespace std;
8
9 const int ONE=500001;
10 const int INF=2147483640;
11
12 int n,m,x;
13 int f[ONE][22],Dep[ONE];
14 int next1[ONE],first1[ONE],go1[ONE],Input[ONE],tot1;
15 int next[ONE],first[ONE],go[ONE],tot;
16 int q[ONE],tou,wei;
17 int size[ONE];
18
19 int get()
20 {
21 int res,Q=1; char c;
22 while( (c=getchar())<48 || c>57)
23 if(c=='-')Q=-1;
24 if(Q) res=c-48;
25 while((c=getchar())>=48 && c<=57)
26 res=res*10+c-48;
27 return res*Q;
28 }
29
30 int Add(int u,int v)
31 {
32 next1[++tot1]=first1[u]; first1[u]=tot1; go1[tot1]=v;
33 Input[v]++;
34 }
35
36 int New_edge(int u,int v)
37 {
38 next[++tot]=first[u]; first[u]=tot; go[tot]=v;
39 }
40
41
42 int LCA(int x,int y)
43 {
44 if(x<0) return y;
45 if(Dep[x]<Dep[y]) swap(x,y);
46 for(int i=20;i>=0;i--)
47 {
48 if(Dep[f[x][i]]>=Dep[y]) x=f[x][i];
49 if(x==y) return x;
50 }
51
52 for(int i=20;i>=0;i--)
53 {
54 if(f[x][i]!=f[y][i])
55 {
56 x=f[x][i];
57 y=f[y][i];
58 }
59 }
60
61 return f[x][0];
62 }
63
64 void Topo()
65 {
66 tou=wei=0;
67 for(int u=1;u<=n;u++)
68 if(!Input[u]) q[++wei]=u;
69 while(tou<wei)
70 {
71 int u=q[++tou];
72 for(int e=first1[u];e;e=next1[e])
73 {
74 int v=go1[e];
75 if(!(--Input[v])) q[++wei]=v;
76 }
77 }
78 }
79
80 void Rebuild()
81 {
82 for(int i=wei;i>=1;i--)
83 {
84 int u=q[i];
85 int To=-INF;
86 for(int e=first1[u];e;e=next1[e])
87 {
88 int v=go1[e];
89 To=LCA(To,v);
90 }
91
92 int v=max(To,0);
93 New_edge(v,u);
94
95 Dep[u]=Dep[v]+1;
96 f[u][0]=v;
97 for(int i=0;i<=19;i++)
98 {
99 f[u][i+1]=f[f[u][i]][i];
100 }
101
102 }
103 }
104
105 int Dfs(int u)
106 {
107 size[u]=1;
108 for(int e=first[u];e;e=next[e])
109 {
110 int v=go[e];
111 Dfs(v);
112 size[u]+=size[v];
113 }
114 }
115
116 int main()
117 {
118 n=get();
119 for(int i=1;i<=n;i++)
120 {
121 for(;;)
122 {
123 x=get();
124 if(!x) break;
125 Add(i,x);
126 }
127 }
128
129 Topo();
130 Rebuild();
131 Dfs(0);
132
133 for(int i=1;i<=n;i++)
134 printf("%d\n",size[i]-1);
135 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号