提升ML.NET模型的准确性

ML.NET是一个面向.NET开发人员的开源、跨平台的机器学习框架。 

使用ML.NET，您可以轻松地为诸如情绪分析、价格预测、销售分析、推荐、图像分类等场景构建自定义机器学习模型。

ML.NET从0.8版开始，支持评估特性的重要性，从而了解哪些列对于预测最终值更重要。 

排列特征的重要性在于，突出最重要的特征，以便理解哪些特征必须包括，哪些不用包括；从数据集中排除一些特性意味着减少噪音，结果会更好。 

因此，通过PFI，我们可以了解在我们的学习pipeline中什么是最重要的列，并使用它们来预测值。

Pipeline

第一步与预测值的步骤相同，因此必须构建pipeline。 

例如，一个标准pipeline可以是这样的：

var mlContext = new MLContext();
var dataView = MlContext.Data.LoadFromTextFile<T>(dataPath, separator, hasHeader: false);
var pipeline = MlContext.Transforms.CopyColumns("Label", _predictedColumn.ColumnName).Append(MlContext.Transforms.Concatenate(_featureColumn, _concatenatedColumns));

这是一个非常简单的pipeline，从文件中加载数据，复制label列并添加feature列。 

现在pipeline已经配置好了，我们可以构建模型了。

Model

建立模型意味着获取pipeline、附加选择算法，对其进行拟合和变换。

var tranformedDataView = pipeline.Append(MlContext.Regression.Trainers.LbfgsPoissonRegression()).Fit(DataView).Transform(DataView);

结果是一个转换后的数据视图，其中应用了pipeline转换所有数据，我们将在Permutation Feature Importance方法中使用这些转换。

Metrics

为了获得PFI指标，除了转换后的数据视图，我们还需要一个转换器：

var transformer = pipeline.MlContext.Regression.Trainers.LbfgsPoissonRegression().Fit(tranformedDataView);

现在我们可以得到度量：

var permutationMetrics = pipeline.MlContext.Regression.PermutationFeatureImportance(transformer, transformedDataView, permutationCount: 3);

使用permutation count参数，我们可以指定希望为回归度量执行的观察次数。

结果是一个回归度量统计数据的数组，并在一个特定的度量上可用的排序，比如平均值：

var regressionMetrics = permutationMetrics.Select((metric, index) => new { index, metric.RSquared }).OrderByDescending(features => Math.Abs(features.RSquared.Mean));

有了循环，我们现在可以打印的指标：

foreach (var metric in regressionMetrics)
{
    if (metric.index >= transformedData.Schema.Count || (transformedData.Schema[metric.index].IsHidden || transformedData.Schema[metric.index].Name == "Label" || transformedData.Schema[metric.index].Name == "Features"))
    continue;
 
    Console.WriteLine($"{transformedData.Schema[metric.index].Name,-20}|\t{metric.RSquared.Mean:F6}");
}

在这个示例的情况下，输出是：

 

 

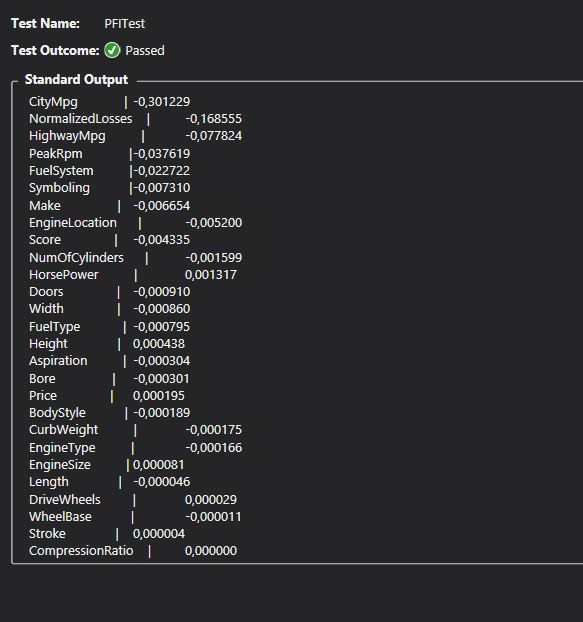
 有了这个统计数据，我们可以了解什么是最重要的特性，并将更改应用到pipeline构建中。

这篇文章的源代码可以在GitHub项目上找到。