[CERC2017]Buffalo Barricades（思维/传递闭图/并查集）
Problem
Solution
首先考虑将每个奶牛归入到最后划分出来的区域，忽略掉一个奶牛可能重复累计到多个区间的条件，例如：
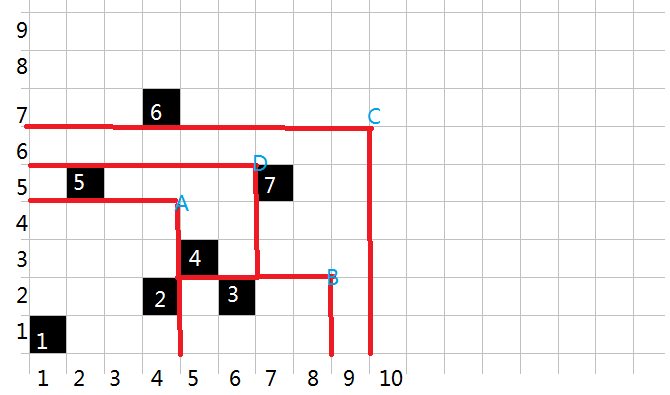
其中奶牛 \(1,2\) 归给操作 \('A'\)，奶牛 \(3\) 归给操作 \('B'\)，以此类推。
用扫描线来实现这一步。我们从右往左扫描每个点，用一个 \(set\) 维护扫描过的栅栏点的 \(y\) 值，且 \(set\) 中维护的栅栏点仍在向左延伸。具体的：
-
如果扫描到一个栅栏点 \(p\)，将其插入到 \(set\)，再一直往下走，如果遇到了比他时间大的点 \(q\)，将 \(q\) 在 \(set\) 中删除，直到遇到第一个比他时间小的点 \(t\)
break。（即第一个 \(y_t<y_p,t<p\)，\(p,t\)是点的编号，直接代表时间） -
如果扫描到一个奶牛点 \(p\)，将其归到 \(set\) 中 \(y\) 值比他大的第一个点 \(t\) 内。
记编号为 \(i\) 的栅栏点经过上述算法统计出来的区间奶牛数为 \(sz_i\)。
我们称包含关系为：区间 \(i\) 包含区间 \(j\)（即 \(x_j<x_i,y_j<x_i\)），且 \(i\) 的时间比 \(j\) 小（即 \(i < j\)），则 \(j\) 对 \(i\) 最后的答案有 \(sz_j\) 贡献。
有了这个关系，我们可以对于每个区间对，如果满足包含关系，则可以 \(j->i\) 建一条边。于是我们得到了一张 \(DAG\)，但是边的数量是 \(n^2\) 的，考虑优化。
可以发现，如果 \(i->j->k\)，则 \(i->k\)，这种关系又叫做传递闭图。可以从这里入手，不建这么多边。具体的： 每个栅栏点 \(j\) 向右上角离它最近的一个点 \(i\) 建一条边，这样建满足了第一维关系（\(x_j<x_i,y_j<x_i\)）。记栅栏点 \(i\) 连向的右上角离它最近的栅栏点为 \(pa[i]\)。这样建出来的图是一个内向森林。
在这个图中，如果 \(i\) 是 \(j\) 的祖先，且 \(j -> i\) 路径上所有的时间都比 \(i\) 大，则可以 \(j\) 对 \(i\) 造成贡献。这个可以按时间从大到小枚举 \(i\)，加入 \(i -> pa[i]\) 这条边。这样扫到 \(j\) 时，\(j\) 的联通块内所有的点的时间都比 \(j\) 大，这样 \(j\) 联通块内所有点 \(k\) 的 \(sz_k\) 都可以对 \(j\) 造成贡献。
时间复杂度 \(O(n \log n)\)。
Code
Talk is cheap.Show me the code.
#include<bits/stdc++.h>
#define pb push_back
#define INF 0x3f3f3f3f
using namespace std;
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
return x * f;
}
const int N = 1e6+7;
int np,n;
int Y[N<<1],sz[N],fa[N],pa[N],ans[N];
struct Node {
int x,id;
bool operator < (const Node &el) const {
return (x==el.x ? id>el.id : x>el.x);
}
}p[N<<1];
int Find(int x) {
return (fa[x]==x ? x : fa[x]=Find(fa[x]));
}
int main()
{
//freopen("")
np = read();
for(int i=1;i<=np;++i) {
int x = read();
Y[i] = read();
p[i] = (Node)<%x,i%>;
}
n = read();
for(int i=np+1;i<=np+n;++i) {
int x = read();
Y[i] = read();
p[i] = (Node)<%x,i%>;
}
sort(p+1, p+1+np+n); //如果x相同 操作需排在点前面
memset(pa, -1, sizeof(pa));
set<Node> s;
for(int i=1;i<=np+n;++i) {
int id = p[i].id, y = Y[id];
if(id <= np) {
//printf("# %d\n",id);
set<Node>::iterator it = s.lower_bound((Node)<%-y,INF%>);
if(it != s.end()) {
Node tmp = *it;
int tid = tmp.id-np;
++sz[tid];
//printf("star %d calc %c\n",id,tid+'A'-1);
}
} else {
//printf("# %c\n",id-np+'A'-1);
set<Node>::iterator it = s.lower_bound((Node)<%-y,INF%>);
if(it!=s.end()) pa[id-np] = it->id-np;
s.insert((Node)<%-y,id%>);
it = s.find((Node)<%-y,id%>);
if(it != s.begin()) --it; //注意
vector<Node> vec;
for(;it!=s.begin();--it) {
if(it->id < id) break;
vec.pb(*it);
}
if(it->id > id) vec.pb(*it);
for(int i=0;i<vec.size();++i) {
s.erase(vec[i]);
}
vec.clear();
}
}
for(int i=1;i<=n;++i) fa[i] = i;
for(int i=n;i>=1;--i) {
int fx = Find(i);
ans[i] = sz[fx];
if(pa[i] != -1) {
int fy = Find(pa[i]);
fa[fx] = fy; sz[fy] += sz[fx];
}
}
for(int i=1;i<=n;++i) printf("%d\n",ans[i]);
return 0;
}
/*
7
1 1
4 2
6 2
5 3
2 5
4 7
7 5
4
4 4
8 2
9 6
6 5
2
1
3
2
*/
Summary
注意 \(set\) 的使用！
