浅谈点分治
简介
点分治就是在一棵树上,对具有某些限定条件的路径静态地进行统计的算法。 ---- 摘自《算法竞赛:进阶指南》
参考资料
感谢以上大佬帮助我学会点分治,如果我这篇blog讲得不够详细也可以参考上述资料。
Problem
先来看一道点分治模板题 -> 洛谷题目地址
- 给定一棵有 \(n\) 个点的无根树,询问树上距离为 \(k\) 的点对是否存在。\(n \le 10^4,k \le 10^7\)。
Solution
设这棵树的根为 \(u\),那么所以的路径可以分为两种,一种是经过 \(u\) 的,另外一种是不经过 \(u\) 的(这种路径就是在 \(u\) 的子树里面)。
例如:
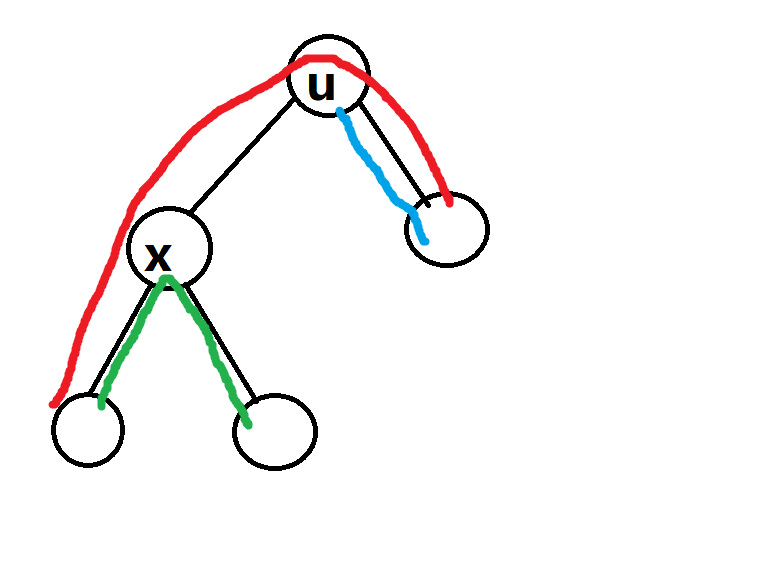
其中红色、蓝色路径就是第一种,绿色路径就是第二种。
进而我们可以发现如果我们以 \(x\) 点为根,那么绿色路径就变为第一种路径了。所以我们关键在于解决第一种情况路径的统计。
在讲解点分治算法之前,我们先来讲述一下如何统计第一种情况的路径:
先对以 \(u\) 为根的树分别对每一个子树进行一遍 \(Dfs\),处理出 \(dist[]\) 数组。并且把所有的路径长度记录下来。
建立 \(bool\) 数组 \(judge[]\),其中 \(judge[i]\) 表示前面子树里面是否出现长度为 \(i\) 的路径。每遍历一个子树,我们循环遍历记录下来的每一个路径长度,看一下 \(judge[K-dist]\) 是否为 \(true\) 就好了。
点分治算法就是(初步):
-
\(1.\) 找到一个点为根,统计所有经过这个点的路径(符合限定条件的)。
-
\(2.\) 删除这个点,递归到下一层,重复 \(1,2\)。
\(Q:\) 点分治算法就这么简单?这样就没有了??
\(A:\) 确实。但是我们来理解一下黑体字“递归到下一层”。理解了这一步你就应该了解点分治算法了。
如下图:

可以发现递归一层的时间复杂度大概是 \(O(N)\) 的。理解?
点分治至此还没有结束,因为我们遇上了难题!!!
设递归层数为 \(T\),那么时间复杂度就是 \(O(TN)\),然而时间复杂度总是能那么优美吗??我们来看一下下面这个例子:

求重心的复杂度是 \(O(N)\),和处理一层的复杂度一样,因此不影响总复杂度。
事实上,有些大佬对点分治的复杂度提出过质疑-->传送门。由于我也没看懂,但是点分治的复杂度应该是不会高于 \(O(NlogN)\)。
最后我们来看一下求重心,点分治你就学会了:
先来看几个概念:
-
\(sum,rt\) :当前这棵树的大小,当前这棵树的根(我们需要求)。
-
\(sz[u]\) :记录当前这棵树上,以u为根的子树大小。
-
\(son[u]\) :\(u\) 的重儿子的大小。重儿子:\(sz[]\) 最大的儿子。
重心:重儿子最小的点。
所以求重心也很简单了,我们来看一下求重心的代码:
void Getrt(int u,int fa) {
sz[u] = 1, son[u] = 0;
for(int i=head[u];i;i=edge[i].next) {
int v = edge[i].to;
if(v == fa || vis[v]) continue; //如果 v 已经处理过(删除),也不用继续访问。
Getrt(v,u);
sz[u] += sz[v];
son[u] = max(son[u],sz[v]);
}
son[u] = max(son[u],sum-sz[u]); //因为是无根树,子树外也是这棵树的一个子树。
if(son[u] < son[rt]) rt = u; //更新重心。
}
一些细节
我们在处理完一个点后,\(judge[]\) 数组也应该要清空。发现值域是 \(10^7\),不能用 \(memset\)。可以用一个队列把处理这个点的时候,修改过的大小记录起来,然后再把修改过的地方重新置为 \(0\)。
最后我们来总结一下点分治的过程:
-
\(1.\) 找到当前树的重心作为根,统计所有经过这个点的路径(符合限定条件的)。
-
\(2.\) 删除这个点,递归到下一层,重复 \(1,2\)。
Code
Talk is cheap.Show me the code.
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
inline int read() {
int x=0,f=1; char ch=getchar();
while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
return x * f;
}
const int N = 1e4+7, M = 107, MAXN = 1e7+7;
int n,m,cnt,sum,rt;
int head[N],K[M],sz[N],son[N],dis[N],mem[N];
bool vis[N],judge[MAXN],ans[M];
struct Edge {
int next,to,w;
}edge[N<<1];
stack<int> q;
inline void add(int u,int v,int w) {
edge[++cnt] = (Edge)<%head[u],v,w%>;
head[u] = cnt;
}
void Getrt(int u,int fa) {
sz[u] = 1, son[u] = 0;
for(int i=head[u];i;i=edge[i].next) {
int v = edge[i].to;
if(v == fa || vis[v]) continue;
Getrt(v,u);
sz[u] += sz[v];
son[u] = max(son[u],sz[v]);
}
son[u] = max(son[u],sum-sz[u]);
if(son[u] < son[rt]) rt = u;
}
void Getdis(int u,int fa) {
mem[++mem[0]] = dis[u];
for(int i=head[u];i;i=edge[i].next) {
int v = edge[i].to, w = edge[i].w;
if(v == fa || vis[v]) continue;
dis[v] = dis[u] + w;
Getdis(v,u);
}
}
void Calc(int u) {
vis[u] = judge[0] = 1;
for(int i=head[u];i;i=edge[i].next) {
int v = edge[i].to, w = edge[i].w;
if(vis[v]) continue;
dis[v] = w; Getdis(v,u);
for(int j=1;j<=mem[0];++j)
for(int l=1;l<=m;++l) {
if(K[l] - mem[j] >= 0)
ans[l] |= judge[K[l] - mem[j]];
}
for(int j=1;j<=mem[0];++j) {
judge[mem[j]] = 1;
q.push(mem[j]);
}
mem[0] = 0;
}
while(!q.empty()) {
judge[q.top()] = 0;
q.pop();
}
}
void Divide(int u) {
Calc(u);
for(int i=head[u];i;i=edge[i].next) {
int v = edge[i].to;
if(vis[v]) continue;
sum = sz[v]; son[rt = 0] = sz[v];
Getrt(v,0); Divide(v);
}
}
int main()
{
//freopen("test.out","w",stdout);
n = read(), m = read();
for(int i=1,u,v,w;i<=n-1;++i) {
u = read(), v = read(), w = read();
add(u,v,w), add(v,u,w);
}
for(int i=1;i<=m;++i) K[i] = read();
son[rt] = sum = n;
Getrt(1,0);
Divide(rt);
for(int i=1;i<=m;++i) {
if(ans[i]) puts("AYE");
else puts("NAY");
}
return 0;
}
题外话:我这份代码在洛谷上只有 \(60pts\),其中有一点 \(RE\),另外一个点 \(TLE\)。\(RE\) 可以见洛谷的讨论贴;\(TLE\) 是因为我用的是 \(STL\) 的队列,用手写队列就不会了。这份代码的思路是没有问题的。
题目
一些简单的点分治题目:
P4178 Tree 洛谷题目地址
- 给定一棵 \(n\) 个节点的树,每条边有边权,求出树上两点距离小于等于 \(k\) 的点对数量。\(n \le 4 \times 10^4,k \le 2 \times 10^4\)。
做法:
关键在于如何统计第一种情况的路径(以 \(u\) 为根,经过 \(u\) 的小于等于 \(k\) 的路径):假设我们用一个数组 \(d[]\),\(d[i]\) 表示前面的子树中等于 \(i\) 的路径的数量,当前遍历到的路径长度是 \(dist\),那么答案就要加上 \(\sum_{i=0}^{K-dist} d[i]\)。发现这是一个需要支持单点修改,区间查询的数据结构,所以我们可以用树状数组。(由于树状数组不能统计 \(0\) 下标,实际做的时候还要注意一些细节。)
P4149 [IOI2011]Race 洛谷题目地址
- 给一棵树,每条边有权。求一条简单路径,权值和等于 \(k\),且边的数量最小。\(n \le 10^4,k \le 10^7\)。
做法:
用一个数组 \(d[]\),\(d[i]\) 不但表示前面子树中长度为 \(i\) 的路径是否存在,还记录一下前面子树中长度为 \(i\) 的路径最少由几条边组成。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号