[HNOI2003]激光炸弹

题目地址

其实就是骗你进来听二维前缀和的，如果你会了就可以出门右转qwq

对于一维前缀和，我们设 \(S[r]=\sum^r_{i=1} a[i]\)，通过递推 \(S[i]=S[i-1]\)，就可以得到 \(S[]\) 数组的值，并且有

\[\text{sum}(l,r)=\sum^r_{i=l}a[i]=S[r]-S[l-1] \]

这里我们来看二维前缀和，其实是一个很好理解的过程

我们设 \(S[x][y]=\sum^x_{i=1}\sum^y_{j=1}a[i][j]\)

我们来看一下 \(S[x-1][y],S[x][y-1],S[x-1][y-1],S[x][y]\)

这是 \(S[x-1][y]\)

这是 \(S[x][y-1]\)

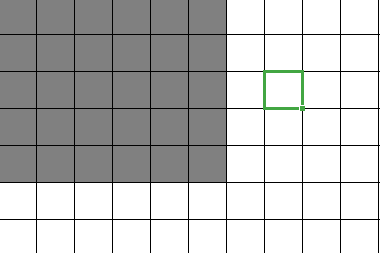
这是 \(S[x-1][y]+S[x][y-1]\) ,中间重叠的部分是 \(S[x-1][y-1]\)

如果我们减去 \(S[x-1][y-1]\)

这下就理解了吧！递推式：

\[S[i][j]=S[i-1][j]+S[i][j-1]-S[i-1][j-1]+a[i][j] \]

这就是大名鼎鼎的 容斥原理 ，如果你像求得一块区间，也要利用同样的思想，剩下的就留给你们自己想吧！

Code

#include<bits/stdc++.h>
#define N 5007
#define INF 0x3f3f3f
using namespace std;
int n,R,ans=-INF;
int val[N][N],sum[N][N];
int main()
{
	scanf("%d%d",&n,&R);
	for(int i=1,x,y,w;i<=n;++i) {
		scanf("%d%d%d",&x,&y,&w);
		val[x+1][y+1] = w;
	}
	for(int i=1;i<=5001;++i)
		for(int j=1;j<=5001;++j)
			sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + val[i][j];
	for(int i=R;i<=5001;++i)
		for(int j=R;j<=5001;++j) {
			int temp = sum[i][j] - sum[i-R][j] - sum[i][j-R] + sum[i-R][j-R];
			ans = max(ans,temp);
		}
	printf("%d\n",ans);
	return 0;
}