贪心算法-射击气球

1、问题描述

　　在二维空间中有许多球形的气球。对于每个气球，提供的输入是水平方向上，气球直径的开始和结束坐标。由于它是水平的，所以y坐标并不重要，因此只要知道开始和结束的x坐标就足够了。开始坐标总是小于结束坐标。平面内最多存在10⁴个气球。

　　一支弓箭可以沿着x轴从不同点完全垂直地射出。在坐标x处射出一支箭，若有一个气球的直径的开始和结束坐标为 x_start，x_end， 且满足  x_start ≤ x ≤ x_end，则该气球会被引爆_。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。

2、问题分析：

　　题目要求使用最少的🗡击中全部的气球，这些气球我们可以抽象的看成是在二位坐标系中的一个一个的线段，这些线段的长度大小不固定，我们已知的就是这些线段的两个横轴坐标。

 

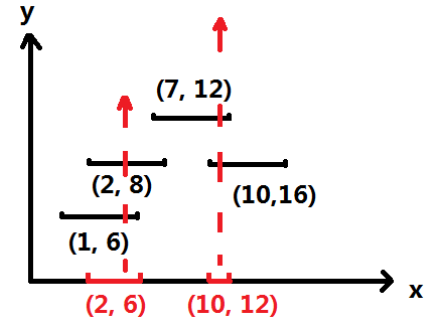
3、算法思想：贪心算法（使用尽可能少的🗡击中尽可能多的气球，只有这样才能保证最后用的🗡的数量是最少的，抽象出来就是我们想办法在这些气球的最大重合区域进行射箭就能满足要求。）

　　1、首先我们把第一个气球（下边全部用线段来代表气球）的长度设置为当前的射箭区域，

　　2、接下来就是比较第二个线段的开始位置和当前射击区域的结束位置的大小关系，只有在第二个线段的开始位置小于当前射击区域的结束位置的时候才能证明这两个线段是有重合关系的；

　　3、在这个前提下（已经确定这两个区域有重合关系，能用一个弓箭射击）比较然后第二个线段的结束位置和当前射击区域的结束位置的大小关系，比较的结果就是把较小的线段位置更新为当前射击区域的结束位置，这是为了维护当前的射击区域一定是这两个线段的公共区域；

　　4、如果不满足2的条件，证明这两个线段没有重合区域，只能增加弓箭的个数。

　　5、针对其他的线段进行按上边叙述的逐个遍历，最后返回弓箭的个数就是最少的弓箭个数。

4、解题代码：

 

package com.baozi.test;

import java.util.Arrays;
import java.util.Comparator;

/**
 * @author BaoZi
 * @create 2019-05-14-10:43
 */
public class Solution1 {
    public static void main(String[] args) {
        int[][] points = new int[][]{{10, 16}, {2, 8}, {1, 6}, {7, 12}};
        int shot_num = Solution1.findMinArrowShots(points);
        System.out.println(shot_num);
    }

    public static int findMinArrowShots(int[][] points) {
        if (points.length == 0) {
            return 0;
        }
        Arrays.sort(points, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return o1[0] - o2[0];
            }
        });
        int short_num = 1;
        int shoot_begin = points[0][0];
        int shoot_end = points[0][1];
        for (int i = 1; i < points.length; i++) {
            if (points[i][0] <= shoot_end) {
                shoot_begin = points[i][0];
                if (points[i][1] < shoot_end) {
                    shoot_end = points[i][1];
                }
            } else {
                short_num++;
                shoot_begin = points[i][0];
                shoot_end = points[i][1];
            }
        }
        return short_num;
    }
}