电磁介质 知识梳理
1.电介质
1.1 极化的微观机制
在一类电介质中,当外电场不存在时,电介质分子的正负电荷中心是重合的,这类分子叫做无极分子;另外一类电介质的正负电荷中心是不重合的,叫做有极分子。
无极分子——位移极化
有极分子——取向极化
1.2 极化强度矢量\(\boldsymbol{P}\)
(1)定义
电极化强度矢量\(\boldsymbol{P}\)等于单位体积内的电矩矢量和
(2)极化电荷的分布
电介质的极化伴随着两个特征:(1)电偶极矩,它由\(\boldsymbol{P}\)描述;(2)极化电荷。可以证明,对于均匀电介质,极化电荷集中在它的表面上。
取一闭合曲面\(\boldsymbol{S}\),令\(\boldsymbol{n}\)为它的外法向矢量,电极化强度矢量为\(\boldsymbol{P}\),\(\boldsymbol{S}\)面内的净极化电荷量为\(\sum q'\),则
对于均匀电介质,其体内无净束缚电荷。电介质表面点电荷层的极化电荷面密度为
1.3 退极化场
电介质极化时出现极化电荷,极化电荷也会在周围空间中产生电场\(\boldsymbol{E'}\),总的空间电场 \(\boldsymbol{E}\)等于外电场\(\boldsymbol{E_0}\)和极化电荷产生的电场\(\boldsymbol{E'}\)的矢量叠加:
极化电荷在电介质内部的附加场\(\boldsymbol{E'}\)总是起着减弱极化的作用,因此也叫做退极化场。
1.4 极化率
电介质任意一点的电极化强度矢量\(\boldsymbol{P}\)是由总电场\(\boldsymbol{E}\)决定的。实验表明,对于大多数常见的各向同性线性电介质,\(\boldsymbol{P}\)与\(\boldsymbol{E}\)满足简单的关系
比例常数\(\chi_e\)叫做极化率,它与场强\(\boldsymbol{E}\)无关,与电介质的种类有关,是介质材料的属性。
外电场\(\boldsymbol{E_0}\longrightarrow\)极化强度\(\boldsymbol{P}\longrightarrow\)极化电荷密度\(\sigma_0\longrightarrow\)退极化场\(\boldsymbol{E'}\longrightarrow\)总电场\(\boldsymbol{E}=\boldsymbol{E'}+\boldsymbol{E_0}\),而总电场\(\boldsymbol{E}\)又会反过来影响极化强度\(\boldsymbol{P}\),可见这些量之间是彼此依赖、相互制约的关系。
1.5 电位移矢量\(\boldsymbol D\) 有电介质时的高斯定理
推导:在有极化电荷存在时,包含自由电荷\(q_0\)和极化电荷\(q'\)的高斯定理写为
电极化强度矢量\(\boldsymbol{P}\)满足
将\((1.5.1)\)乘以\(\varepsilon_0\),再加上\((1.5.2)\)得
现在引入一个辅助性的矢量\(\boldsymbol{D}\)
\(\boldsymbol{D}\)即电位移矢量。上述公式简记为
\((1.5.3)\)式的优越性在于它不包含极化电荷\(q'\)。对于各向同性电介质,代入\(\boldsymbol{P}=\chi_e\varepsilon_0\boldsymbol{E}\)
正式引入相对介电常数:
利用新的高斯定理,可以先把\(\boldsymbol{D}\)求出,然后根据\(\boldsymbol{D}\)和总电场、总电场和附加电场之间的关系求出其余各量。
一个有趣的问题:无电介质时的静电场高斯定理为
加入电介质后的高斯定理为
比较以上两式的数学形式,是否可以认为\(\boldsymbol{D}\)就是\(\boldsymbol{E_0}\)的\(\varepsilon_0\)倍呢?否! 事实上,\(\boldsymbol{D}=\varepsilon_0\boldsymbol{E_0}\)成立的前提是:均匀电介质充满存在电场的全部空间,或者均匀电介质的表面为等势面。问题就出在,高斯定理并不能将矢量场的分布完全确定下来,它反映的只是矢量场的一个方面。反映矢量场的另一个侧面的是环路定理
但是电位移矢量的环路积分\(\oint\boldsymbol{D\cdot}{\rm d}\boldsymbol{l}\)往往不等于0,这也就意味着\(\boldsymbol{D}\)往往不等于\(\varepsilon_0\boldsymbol{E}_0\)。
2. 磁介质(一)——分子电流观点
2.1 磁介质的磁化
有关磁介质(例如铁芯)磁化的理论,有两种不同的观点——分子电流观点和磁荷观点。二者基于的微观模型不同,但是最后得到的计算结果是完全相同的。
分子电流观点:即安培的分子环流假说。以一段插在线圈中的软铁棒为例。未通电的情况下,铁棒内每个分子的环流的方向是杂乱无章的,在宏观上不显示磁性。线圈通电后,在外加的磁化场的作用下,各分子环流的磁矩趋向于向外加磁场的方向排列,这时我们就称铁棒被磁化了。在介质内部,任何两个相邻(径向相邻)的分子环流的电流方向是相反的,结果相互抵消。只有在横截面边缘的电流元没有被抵消,因而宏观上来看,被磁化的软铁棒就如同一个由一环环电流组成的螺线管。“螺线管”在内部产生的磁场方向与外加磁场方向一致,因此铁芯能够使磁通量增加。
2.2 磁化强度矢量\(\boldsymbol{M}\)
(1)定义
为了描述磁介质的磁化状态,引入磁化强度矢量的概念,它定义为单位体积内分子磁矩的矢量和。
(2)磁化电流的分布与磁化强度的关系
这就是与\((1.5.2)\)式对应的磁介质公式,它是反映磁介质中磁化电流\(I'\)的分布与磁化强度之间联系的普遍公式。
与电介质的极化电荷分布密度\(\sigma_e=\boldsymbol{P\cdot}\boldsymbol{n}\)对应的公式为
其中:
\(\boldsymbol{i'}\):介质表面单位长度上的磁化电流,也叫面磁化电流密度;
\(\boldsymbol{n}\):磁介质表面的外法向单位矢量。
2.3 磁介质内的磁感应强度矢量\(\boldsymbol{B}\)
类似于电介质的情况,磁介质内的总磁感应强度\(\boldsymbol{B}\)由外加\(\boldsymbol{B}\)和附加的\(\boldsymbol{B'}\)合成
不过现在的附加磁场\(\boldsymbol{B'}\)往往起加强作用,比如被磁化的软铁棒,它产生的附加磁场与原磁场方向相同。
2.4 磁场强度矢量\(\boldsymbol{H}\) 有磁介质时的安培环路定理
对标有电介质存在的高斯定理,先考虑有磁介质的安培环路定理
以及磁介质公式
消去磁化电流的项得到
引入辅助矢量磁场强度矢量\(\boldsymbol{H}\)
即得
特别地,在真空中无磁介质,\(\boldsymbol{H}=0\),此时得磁感应强度和磁场强度矢量之间的关系为
磁场强度矢量\(\boldsymbol{H}\)的单位是\(\rm A/m\)。另一种常用单位是奥斯特,用\(\rm Oe\)表示,换算关系是
3. 磁介质(二)——磁荷观点
磁的理论最初是建立在磁的1库仑定律上的,也就是磁荷观点。它将磁极看成是磁荷聚集的地方,小磁针是磁偶极子。分子电流则是后来才建立的理论,二者相互等价。
3.1 磁介质的磁化 磁极化强度矢量\(\boldsymbol{J}\)
仍以铁芯为例。在磁荷观点看来,磁介质的最小单元是磁偶极子,当介质未磁化时,磁偶极子的分布是杂乱无章的,整体上不显示磁性。给线圈通电后,线圈产生一个磁场\(\boldsymbol{H}_0\),叫做磁化场,磁化场使得铁棒中的磁偶极子整齐地排列起来。在介质内部,磁偶极子首尾相接,相互抵消,只有在铁棒的两个端面上出现N、S极。
磁极化强度矢量\(\boldsymbol{J}\)定义为单位体积内分子磁偶极矩的矢量和。
3.2 磁荷分布与磁极化强度矢量\(\boldsymbol{J}\)的关系
3.3 退磁场与退磁因子
(1)退磁场
当介质棒被磁化以后,在其两端出现N、S两极,这两极在介质内部产生的磁场\(\boldsymbol{H'}\)与磁化场\(\boldsymbol{H}_0\)方向相反,因此叫做退磁场。退磁场越大,介质越不容易磁化。
(2)退磁因子
退磁场与磁极化强度成正比:
\(N_D\)称为介质棒的退磁因子,在这里是一个无量纲的数。
只有椭圆形的磁介质才能在均匀外磁场中均匀磁化,而有限长的圆柱形磁介质在均匀外磁场中的磁化也是不均匀的。
3.4 安培环路定理 高斯定理
总磁场\(\boldsymbol{H}=\boldsymbol{H}_0+\boldsymbol{H'}\),下面分别讨论\(\boldsymbol{H}_0\)和\(\boldsymbol{H'}\)的环路定理和高斯定理。
(1)磁化场\(\boldsymbol{H}_0\)由电流产生,服从毕奥-萨伐尔定律,将以前得到的结论中的\(\boldsymbol{B}\)替换为\(\mu_0\boldsymbol{H}\)得
(2)附加场\(\boldsymbol{H'}\)由磁荷产生,服从库仑定律,对应的环路定理和高斯定理同静电场
综合以上两部分,得到总磁场\(\boldsymbol{H}\)满足的安培环路定理和高斯定理
3.5 磁感应强度矢量\(\boldsymbol{B}\)
对标电介质中的电位移矢量,在磁场中,将下式
与\(\boldsymbol{H}\)满足的高斯定理联立消去\(\sum q_m\)得到
引入辅助性的矢量\(\boldsymbol{B}\),它的定义为
这个\(\boldsymbol{B}\)正是磁感应强度矢量。这样就从磁荷的角度引入了\(\boldsymbol{B}\)。在真空中,\(\boldsymbol{J}=0\),有
利用\(\boldsymbol{B}\)的定义得到
这就是与有电介质时的高斯定理对应的公式。对比之下,该式的右侧为零,原因是没有“自由磁荷”,即所谓“磁单极子”,所有的N极和S极都是成对出现的,类似于束缚电荷中所有的正电荷和负电荷都是成对出现的。
综上所述,从磁荷的观点得到磁场的两个普遍的公式:
\(\boldsymbol{H}\)矢量的环路定理
\(\boldsymbol{B}\)矢量的高斯定理
3.6 磁化率和磁导率
仿照极化强度\(\boldsymbol{P}\)与电场强度\(\boldsymbol{E}\)的关系式
引入磁极化强度\(\boldsymbol{J}\)与磁场强度\(\boldsymbol{H}\)的关系
其中\(\chi_m\)叫做磁化率。它对应电介质中的介电常数\(\varepsilon\)。
其中
称为相对磁导率,它与电介质中的相对介电常量\(\varepsilon\)对应。
4. 磁介质两种观点与电介质的对比
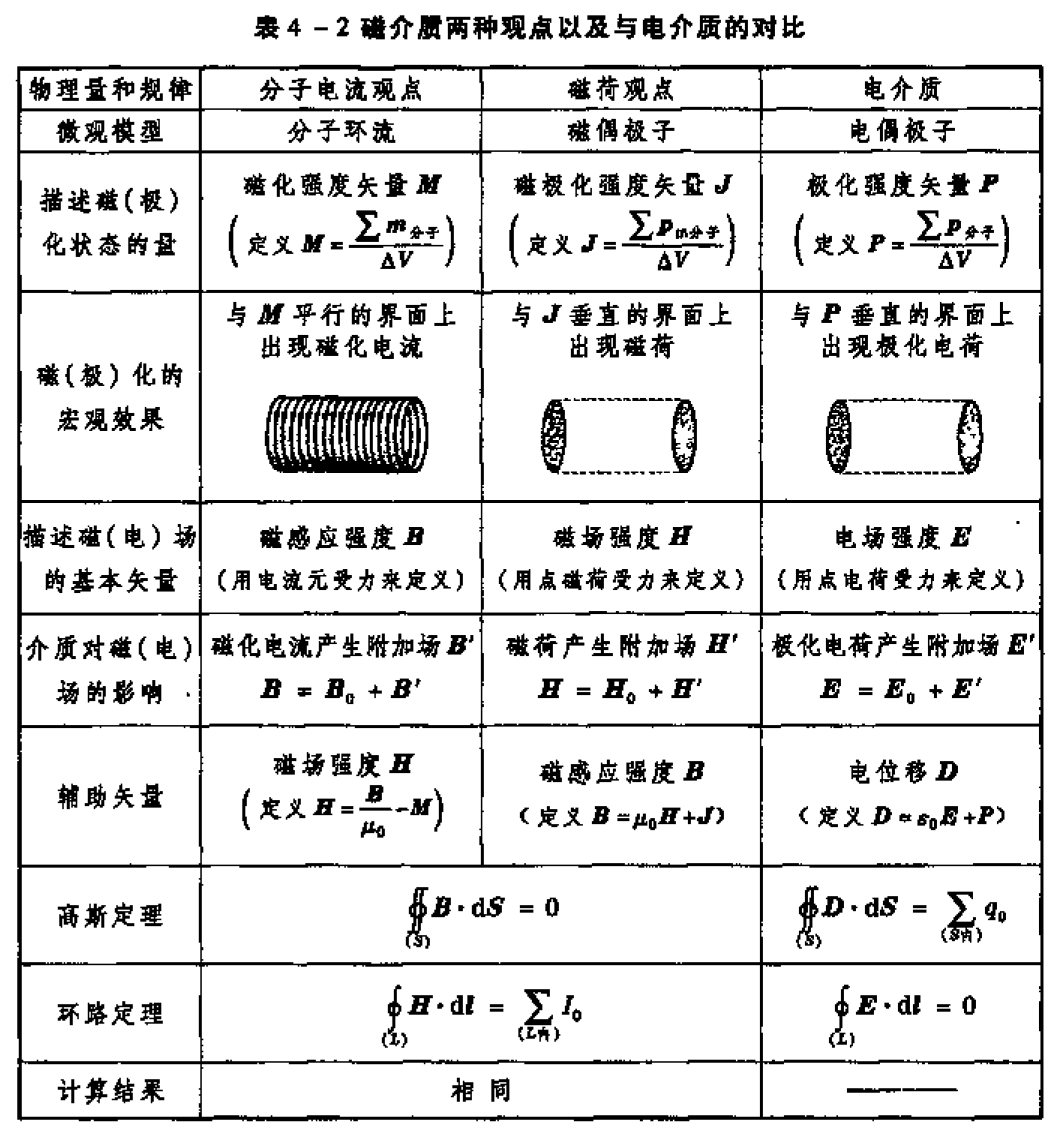
5. 磁介质的磁化规律和机理 铁电体
5.1 磁介质的分类
磁介质大体可以分为顺磁质、抗磁质、铁磁质三类。对于顺磁质,\(\chi_m > 0\),\(\mu>1\);对于抗磁质,\(\chi_m < 0\),\(\mu<1\)。
以上两类的磁介质的磁性都很弱,\(|\chi_m|\ll1\),而且都是与\(\boldsymbol{H}\)无关的常数。铁磁质的情况很复杂,一般来说\(M\)和\(H\)不成比例,它还与磁化的历史有关。铁磁质的\(\chi_m\)和\(\mu\)的值一般都很大,量级为\(10^2\)~\(10^3\),甚至\(10^6\)以上。
5.2 顺磁质和抗磁质
(1)顺磁质:分子有固有磁矩,取向磁化。
(2)抗磁质:分子无固有磁矩,洛伦兹力产生感生磁矩。
5.3 铁磁质的磁化规律
铁磁质是以铁为代表的一类磁性很强的物质。常用的铁磁质多数是铁和其他金属或非金属组成的合金,以及某些包含铁的氧化物(铁氧体)。
铁磁质的磁化规律通常是在没有退磁场的闭合铁芯螺线环中测的。起始磁化曲线如下
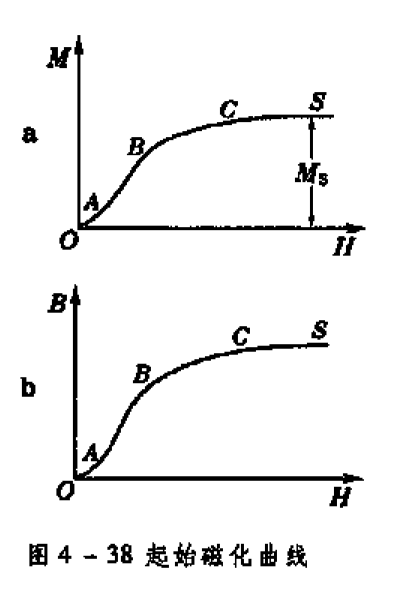
\(OA\):缓慢增加
\(AB\):急剧增加
\(BC\):缓慢增加
\(CS\):饱和
饱和时的磁化强度称为饱和磁化强度,用\(M_S\)表示。
由\(\boldsymbol{M}\)、\(\boldsymbol{B}\)和\(\boldsymbol{H}\)之间的关系
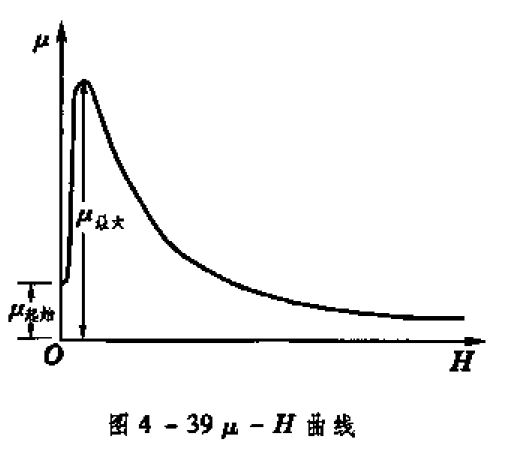
可见,\(M-H\)曲线和\(B-H\)曲线上某一点与原点连线的斜率分别代表该点上的磁化率\(\chi_m\)和磁导率\(\mu\mu_0=(1+\chi_m)\mu_0\)。可以得到结论:当\(H\)的数值从0开始增加时,\(\chi_m\)和\(\mu\)由一初始值开始增加(\(\mu_{起始}\)),然后达到一个最大值(\(\mu_{最大}\)),之后由于磁化接近饱和,再增大\(H\)反而会使磁化率减小。
关键:起始磁导率,最大磁导率,饱和磁化强度
(2)磁滞回线
退磁曲线由饱和退到剩余磁化状态——剩余磁化强度\(\boldsymbol{M}_R\);
反向磁场使磁化强度降为0——矫顽力\(\boldsymbol{H}_C\);
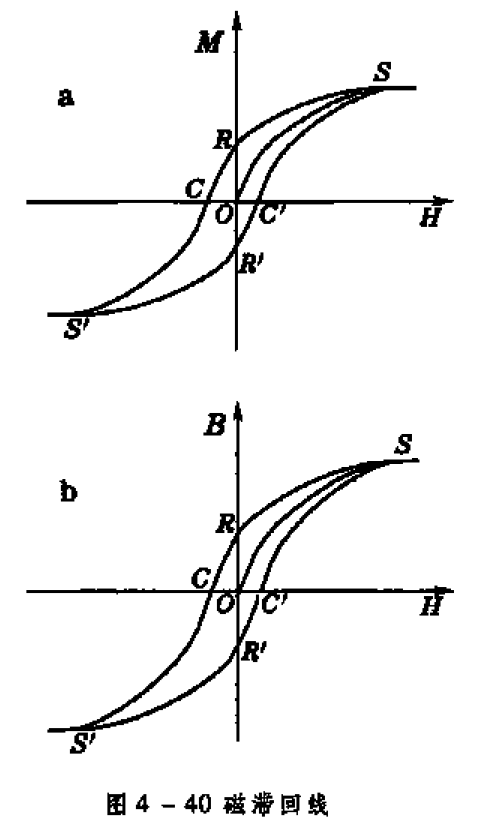
5.4 磁滞损耗
\(B-H\)图中磁滞回线所包围的面积代表在一个反复磁化的循环过程中单位体积的铁芯内损耗的能量。这部分能量最终将以热的形式损耗掉。
5.5 铁磁质的分类
按照矫顽力的大小分为软磁材料和硬磁材料两大类。矫顽力很小的叫做软磁材料;矫顽力大的叫做硬磁材料。
软磁材料:磁滞损耗小,适用于交变磁场中,例如电子设备中的各种电感元件,变压器的铁芯。,继电器的铁芯。
硬磁材料(永磁体):剩余磁化强度大,矫顽力大,最大磁能积大。
6. 电磁介质界面上的边界条件 磁路定理
在两种电介质的界面两侧:
- 电位移矢量\(\boldsymbol{D}\)的法向分量连续;
- 电场强度矢量\(\boldsymbol{E}\)的切向分量连续。
在两种磁介质的界面两侧:
- 磁感应强度矢量\(\boldsymbol{B}\)的法向分量连续;
- 磁场强度矢量\(\boldsymbol{H}\)的切向分量连续。
电场线和磁感线在界面上的折射遵循的规律基本相同。一个有用的结论是:高磁导率的物质(如铁磁材料)会把磁通量集中到自己内部。
磁路定理
铁芯可以把绝大部分磁通量集中到自己内部。铁芯构成的磁感应管叫做磁路。磁路可以类比电路。由安培环路定理得
闭合积分回路\(L\)沿着磁路选取。因为每一段磁路上的磁通量都一样,不妨记为\(\Phi_B\)。上式改写成
与闭合电路的情况相对比:
磁通势(磁动势)\(\varepsilon_m=NI_0\)
磁阻\(R_{mi}=l_i/{\mu_i\mu_0S_i}\)
7. 电磁场能
7.1 电场的能量和能量密度
对于各向同性电介质,电场的能量密度
在\(\boldsymbol{D}\)和\(\boldsymbol{E}\)方向不同的情况下
7.2 磁场的能量和能量密度
磁能密度:

