电磁学 数学储备

A 矢量的乘积和对称性

\[\def\ooint{{\bigcirc}\kern-11.5pt{\int}\kern-6.5pt{\int}} \def\oooint{{\bigcirc}\kern-12.3pt{\int}\kern-7pt{\int}\kern-7pt{\int}} \]

矢量的标积

设\(\boldsymbol{A}\)和\(\boldsymbol{B}\)是两个任意矢量，则他们的标积定义为

\[\boldsymbol{A \cdot B} = A_xB_x+A_yB_y+A_zB_z \]

矢量的矢积

设\(\boldsymbol{A}\)和\(\boldsymbol{B}\)是两个任意矢量,则他们的矢积定义为如下矢量

\[\boldsymbol{A\times B}= \begin{vmatrix} \boldsymbol{i} & \boldsymbol{j}&\boldsymbol{k} \\\\ A_x & A_y & A_z \\\\ B_x & B_y & B_z \end{vmatrix} \]

矢量的三重积

(1)三重标积\(\boldsymbol{A\cdot}(\boldsymbol{B \times C})\)
这种三重积是一个标量,解析式为

\[\boldsymbol{A\cdot}{(\boldsymbol{B\times C})}= \begin{vmatrix} A_x & A_y & A_z \\\\ B_x & B_y & B_z \\\\ C_x & C_y & C_z \end{vmatrix} \]

几何意义:这个三重积的绝对值等于以\(\boldsymbol{A},\boldsymbol{B},\boldsymbol{C}\)三矢量为棱组成的平行六面体的体积.三个矢量可以轮换,只要循环次序不变,结果就不变

\[\boldsymbol{A\cdot}(\boldsymbol{B\times C}) =\boldsymbol{B\cdot}(\boldsymbol{C\times A}) =\boldsymbol{C\cdot}(\boldsymbol{A\times B}) \]

(2)三重矢积\(\boldsymbol{A\times}(\boldsymbol{B\times C})\)
这种三重积是一个矢量.由于\(\boldsymbol{B\times C}\)的结果与\(\boldsymbol{B},\boldsymbol{C}\)平面垂直,那么\(\boldsymbol{A}\)叉乘以后的最终结果就又回到了该平面内,也就是说

\[\boldsymbol{A\times}(\boldsymbol{B\times C})=\alpha_1 \boldsymbol{B}+\alpha_2\boldsymbol{C} \]

存在恒等式

\[\boldsymbol{A\times}(\boldsymbol{B\times C})=(\boldsymbol{A\cdot C})\boldsymbol{B}-(\boldsymbol{A\cdot B})\boldsymbol{C} \]

一般正交曲线坐标系的概念

任何描述三维空间的坐标系都要有三个独立的坐标变量\(u_1,u_2,u_3\).例如,在直角坐标系中,\(u_1=x,u_2=y,u_3=z\).下列方程式

\[ \begin{cases} u_1 =Constant\\ u_2 = Constant \\ u_3 = Constant \\ \end{cases} \]

代表三组曲面,称为坐标面.若三组坐标面在空间的每一点正交,则坐标面的交线也在空间的每一点正交,这种坐标系叫做正交曲线坐标系(orthogonal curvilinear coordinate system).在空间的每一点可以沿三条交线的方向各取一个单位矢量,这三个矢量\(\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3\)叫做坐标系的单位基矢.直角坐标系可以看作正交曲线坐标系的一个特例,它的单位基矢方向是恒定不变的.在一般的正交曲线坐标系中,单位基矢的方向可能逐点变化,但在每一点仍保持正交.常见的正交曲线坐标系有球坐标系,柱坐标系,抛物线坐标系和椭圆坐标系等.

沿三个基矢的线段元\({\rm d}l_1,{\rm d}l_2,{\rm d}l_3\)分别与三坐标变量的微分\({\rm d}u_1,{\rm d}u_2,{\rm d}u_3\)成正比

\[\begin{cases} {\rm d}l_1 = h_1{\rm d}u_1 \\ {\rm d}l_2 = h_2{\rm d}u_2 \\ {\rm d}l_3 = h_3{\rm d}u_3 \\ \end{cases} \]

在直角坐标系中, \(h_1= h_2= h_3=1\),但在一般的正交曲线坐标系中,它们往往不等于1.

柱坐标系

在原有的直角坐标系的基础上定义柱坐标系(Cylindrical coordinate system),如图1,可以用三个变量\((r,\varphi,z)\)描述坐标系中的任意一点.柱坐标系相当于在极坐标系的基础上增加了一根垂直轴.

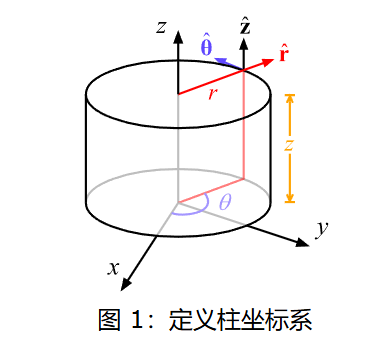
柱坐标系的三个变量为

\[u_1=\rho,\quad u_2=\varphi,\quad u_3=z \]

柱坐标系与直角坐标系之间的变换关系为

\[\begin{equation*} \left\{ \begin{aligned} &x=\rho \cos \varphi ,\\ &y=\rho\sin\varphi ,\\ &z=z. \end{aligned} \right. \quad \begin{cases} \rho= \sqrt{x^2+y^2} \\ \varphi=\arctan \frac{y}{x} \\ z= z\\ \end{cases} \end{equation*} \]

柱坐标系三个变量的取值范围是

\[0\leq\rho<+\infty,\quad 0\leq\varphi<2\pi,\quad -\infty<z<+\infty \]

柱坐标系的三个坐标面为

1. \(\rho=Constant\),这是以z轴为轴线的圆柱.
2. \(\varphi=Constant\),这是通过\(z\)轴的半平面.
3. \(z=Constant\),这是与\(z\)轴垂直的平面.

显然,三组坐标面彼此正交,属于正交曲线坐标系.柱坐标系中的三个基矢分别为\(\boldsymbol{e_{\rho}},\boldsymbol{e_{\varphi}},\boldsymbol{e_z}\),则沿基矢方向的三个线段元为

\[{\rm d}l_{\rho}={\rm d}\rho,\quad {\rm d}l_{\varphi}=\rho{\rm d}\varphi,\quad {\rm d}l_z = {\rm d}z \]

对照得

\[h_{\rho}=1,\quad h_{\varphi}=\rho,\quad h_z=z \]

与直角坐标系不同,现在的单位基矢是关于坐标的函数.

球坐标系

球坐标系往往在直角坐标系的基础上定义,三维直角坐标系中的任意一点\(\boldsymbol{P}\)的位置都可以用\((r,\theta,\varphi)\)这三个有序实数来表示,称为该点的球坐标系(spherical coordinates).其中\(r\)表示该点到原点的距离(\(r\geq0\)),即位矢的模长;\(\theta\)表示该点的位矢与\(z\)轴的夹角,(\(\theta\in [0,\pi]\)),即极角(polar angle).\(\varphi\)表示该点的位矢与\(x-y\)平面上的投影与\(x\)轴的夹角,即方位角(azimuthal angle).显然,球坐标系的三个坐标面也互相垂直.

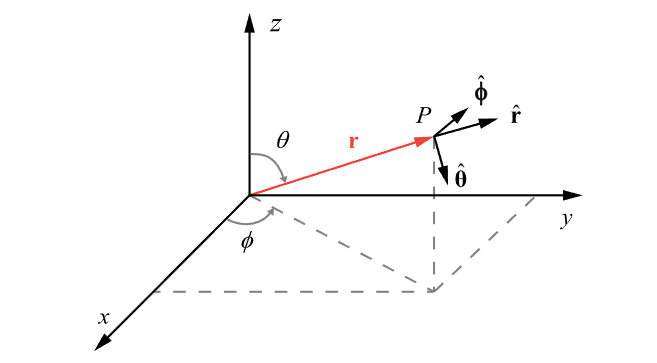
三个球坐标分别对应单位矢量\(\boldsymbol{e}_r,\boldsymbol{e}_\theta,\boldsymbol{e}_\varphi\)(或者\(\boldsymbol{\hat{r}},\boldsymbol{\hat{\theta}},\boldsymbol{\hat{\phi}}\))彼此正交.定义它们的方向分别指向对应坐标增加的方向,任意三维矢量都可以表示成它们的线性组合

\[\boldsymbol{A}=A_r\boldsymbol{e}_r+A_\theta\boldsymbol{e}_\theta+A_\varphi\boldsymbol{e}_\varphi \]

另外,球坐标的三个坐标按照\((r,\theta,\varphi)\)排序,是为了使单位矢量满足

\[\boldsymbol{\hat{r}} \boldsymbol{\times} \boldsymbol{\hat{\theta}} = \boldsymbol{\hat{\phi}} \]

可以类比直角坐标系的三个单位矢量必须满足\(\boldsymbol{i\times j}=\boldsymbol{k}\).这也是对所有正交曲线坐标系的要求.

在球坐标系中沿基矢方向的三个线段元为

\[{\rm d}l_r = {\rm d}r,\quad {\rm d}l_\theta=r{\rm d}\theta,\quad {\rm d}l_\phi=r\sin\theta{\rm d}\phi; \]

\[h_r=1,\quad h_\theta=r,\quad h_\phi=r\sin\theta \]

B 矢量分析提要

参考:矢量分析总结-小时百科

标量场和矢量场

\((1)\)标量场
含义:标量场,就是在空间各点存在着的一个标量\({\Phi}\),它的数值是空间位置的函数.

\[\Phi = \Phi(x,y,z) \]

等值面,就是下列方程式的轨迹

\[\Phi=Constant \]

\((2)\)矢量场
含义:矢量场,就是在空间各点存在着的一个矢量,它的大小和方向是空间位置的函数.

\[\boldsymbol{A}=\boldsymbol{A}(x,y,z) \]

场线:有方向的曲线,其上每一点切线的方向都与\(\boldsymbol{A}\)的方向一致.
场管：由一束场线围城的管状区域。

标量场的梯度

\((1)\)定义
标量场的梯度定义为这样一个矢量,它沿方向微商最大的方向,数值上等于这个最大的方向微商,通常记作\({\rm grad}\Phi\)或\(\nabla\Phi\).

\[\nabla\Phi = \frac{\partial\Phi}{\partial n} \]

标量场的梯度是矢量场.
\((2)\)坐标表示式
在正交曲线坐标系中,标量场梯度的一般表达式为

\[\nabla U=\frac{1}{h_1}\frac{\partial U}{\partial u_1}\boldsymbol{e}_1+\frac{1}{h_2}\frac{\partial U}{\partial u_2}\boldsymbol{e}_2+\frac{1}{h_3}\frac{\partial U}{\partial u_3} \]

矢量场的通量和散度 高斯定理

\((1)\)定义
矢量场\(\boldsymbol{A}\)通过一个截面\(\boldsymbol{S}\)的通量\(\Phi_A\)定义为

\[\Phi_A = \iint_{(S)} \boldsymbol{A\cdot{\rm d}S} \]

令\(\boldsymbol{S}\)为一闭合曲面,它包含的体积为\(\Delta V\),设想\(S\)面逐渐缩小到空间某点\(P\),则\(\boldsymbol{A}\)在该曲面上的通量也趋近于0.若通量与体积之比的极限存在,将这个极限定义为矢量场\(\boldsymbol{A}\)在\(P\)点的散度

\[{\rm div}\boldsymbol{A}=\boldsymbol{\nabla\cdot A}=\lim_{\Delta V\to 0}\frac{\Phi_A}{\Delta V} \]

矢量场的散度是标量场.
\((2)\)散度的坐标表示

\[\boldsymbol{\nabla\cdot A}=\frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z} \]

\((3)\)高斯定理

\[\ooint_S \boldsymbol{A\cdot{\rm d}S}=\iiint_V \boldsymbol{\nabla\cdot}\boldsymbol{A}{\rm d}V \]

矢量场通过任意闭合曲面\(S\)的通量,等于它所包围的体积\(V\)内散度的积分.

矢量场的环量和旋度 Stokes定理

\((1)\)定义
矢量场\(\boldsymbol{A}\)沿闭合回路的积分称为环量:

\[\it\Gamma_A = \oint_L \boldsymbol{A\cdot}{\rm d}\boldsymbol{l} \]

令\(\Delta S\)为闭合曲线包围的面积,\(\boldsymbol{n}\)为\(\Delta S\)的右旋单位法向矢量.设想回路逐渐缩小,最后缩到空间某点\(P\),则\(\it\Gamma_A\)也会随之趋近于0.若环量\(\it\Gamma_A\)与面积\(\Delta S\)之比有一个极限,则这极限值为矢量场\(\boldsymbol{A}\)的旋度在\(\boldsymbol{n}\)上的投影.\(\boldsymbol{A}\)的旋度为

\[(\boldsymbol{\nabla\times}\boldsymbol{A})_n=\lim_{\Delta S\to 0}\frac{\oint \boldsymbol{A\cdot}{\rm d}\boldsymbol{l}}{\Delta S} \]

\((2)\)旋度的坐标表达式

\[\boldsymbol{\nabla\times}\boldsymbol{A}= \begin{vmatrix} \boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\\\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\\\ A_x & A_y & A_z \\ \end{vmatrix} \]

\((3)\)Stokes定理

\[\oint_L \boldsymbol{A\cdot}{\rm d}\boldsymbol{l}= \iint_S (\boldsymbol{\nabla\times}\boldsymbol{A})\boldsymbol{\cdot}\boldsymbol{{\rm d}S} \]

矢量场在任意闭合回路上的环量,等于以它为边界的曲面上旋度的积分.

矢量场的类别和分解

\((1)\)有散场和无散场
散度为0,即无源,为无散场;散度不为0,即有源,为有散场.由公式

\[\boldsymbol{\nabla\cdot}\boldsymbol{\nabla\times}\boldsymbol{A}=0 \]

知,任何矢量场的旋度永远是无散场.
反之亦然,任何无散场\(\boldsymbol{B}\)可以表示成某个矢量场\(\boldsymbol{A}\)的旋度.

\((2)\)有旋场和无旋场
旋度为 0,为无旋场;反之为有旋场.由公式

\[\boldsymbol{\nabla\times}\boldsymbol{\nabla}\Phi=0 \]

知,任何标量场的梯度永远是个无旋场.
反之亦然,任何无旋场\(\boldsymbol{A}\)可以表成某个标量场\(\Phi\)的梯度

\[\boldsymbol{\nabla\times}\boldsymbol{A}=0,\quad \boldsymbol{A}=\boldsymbol{\nabla\Phi} \]

\(\Phi\)为无旋场\(\boldsymbol{A}\)的势函数,故无旋场又称为势场.
\((3)\)谐和场
若一矢量场\(\boldsymbol{A}\)在某空间范围内既无散又无旋,则这矢量场称为谐和场.设矢量场的势函数为\(\Phi\),由无旋可知

\[\boldsymbol{\nabla\times}\boldsymbol{A}=0,\quad \boldsymbol{A}=\boldsymbol{\nabla\Phi} \]

再由无散可知

\[\boldsymbol{\nabla\cdot}\boldsymbol{A}=\boldsymbol{\nabla\cdot}\boldsymbol{\nabla\Phi}=0 \]

即

\[\boldsymbol{\nabla}^2 \Phi=0 \]

上式叫做拉普拉斯方程.谐和场的势函数满足拉普拉斯方程.
\((4)\)一般矢量场的分解
在普遍的情形下,一个矢量场\(\boldsymbol{A}\)可以既是有旋的,又是有散的.在这种情况下\(\boldsymbol{A}\)可以分解为两部分

\[\boldsymbol{A}=\boldsymbol{A}_势+\boldsymbol{A}_旋 \]

\(\boldsymbol{A}_势\):势场,即无旋场;
\(\boldsymbol{A}_旋\):无散的有旋场.
上述分解并不唯一,其中可以相差一个任意的谐和场.
参考链接:矢量算符运算法则