# 预测财政收入,2014、2015(y) 神经网络,用到data_1
import os
import numpy as np
import pandas as pd
from sklearn.linear_model import LassoLars
from sklearn.linear_model import Lasso
from keras.models import Sequential
from keras.layers.core import Dense, Activation
import matplotlib.pyplot as plt
filepath = "C:/Users/Lenovo/Desktop/data(1).csv"
data = pd.read_csv(filepath)
l=['x3','x5','x7','x11','y']
data_1=data[l].copy()
print(data_1)
data_1.index = range(1994,2014)
data_train=data_1.loc[range(1994,2014)].copy()
data_train_normal=(data_train-data_train.mean())/data_train.std() # 数据标准化,按列索引(列名)计算
y_class=l.pop()
x_train=data_train_normal[l] # 特征数据提取
y_train=data_train_normal[y_class] #标签数据提取
# 构造神经网络模型
nn_model=Sequential() # create the NN-model
nn_model.add(Dense(input_dim=4,units=12)) #
nn_model.add(Activation('relu')) #
nn_model.add(Dense(1)) # 最后一层不激活,直接输出。或者说把激活函数看作f(x)=x
nn_model.compile(loss='mean_squared_error', optimizer='adam',metrics=['accuracy'])
#net.fit(train_data[:,:3],train_data[:,3],epochs=10,batch_size=1)#keras 2.0之前版本
nn_model.fit(x_train,y_train,epochs=1000,batch_size=16,verbose=1)#keras 2.0,推荐,verbose=0,不显示过程,默认等于1显示过程
# 预测,还原结果
x=((data_1[l]-data_train[l].mean())/data_train[l].std()).values
data_1['y_pred']=nn_model.predict(x)*data_train['y'].std()+data_train['y'].mean()
# GM模型,预测
def GM11(x0): #自定义灰色预测函数
x1 = x0.cumsum() #1-AGO序列
x1 = pd.DataFrame(x1)
z1 = (x1 + x1.shift())/2.0 #紧邻均值(MEAN)生成序列
z1 = z1[1:].values.reshape((len(z1)-1,1)) # 转成矩阵
B = np.append(-z1, np.ones_like(z1), axis = 1) # 列合并-z1和形状同z1的1值矩阵 19X2
Yn = x0[1:].reshape((len(x0)-1, 1)) # 转成矩阵 19
[[a],[b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Yn) #计算参数,基于矩阵运算,np.dot矩阵相乘,np.linalg.inv矩阵求逆
f = lambda k: (x0[0]-b/a)*np.exp(-a*(k-1))-(x0[0]-b/a)*np.exp(-a*(k-2)) #还原值
delta = np.abs(x0 - np.array([f(i) for i in range(1,len(x0)+1)])) # 残差绝对值序列
C = delta.std()/x0.std()
P = 1.0*(np.abs(delta - delta.mean()) < 0.6745*x0.std()).sum()/len(x0)
return f, a, b, x0[0], C, P #返回灰色预测函数、a、b、首项、方差比、小残差概率
#ax1=plt.subplot(211)
#ax1.plot(data_1['y'],'b-o')
#ax1.legend()
#ax2=plt.subplot(212)
#ax2.plot(data_1['y_pred'],'r-*')
#ax2.legend()
plt.plot(data_1['y'],'b-o')
plt.plot(data_1['y_pred'],'r-*')
plt.legend()
# # 政府性基金收入采用GM11预测2006-2015年份收入,并和原值2006-2013比较
x0 = np.array([3152063, 2213050, 4050122, 5265142,5556619, 4772843,9463330])
f, a, b, x00, C, P = GM11(x0) # 得到预测函数f,可计算接下来预测值(和序号相关,按序预测)
len(x0)
p=pd.DataFrame(x0,index=range(2007,2014),columns=['y']) # 'y'要带上中括号
p.loc[2014]=None
p.loc[2015]=None
p['y_pred']=[f(i+1) for i in range(len(p))]
p=p.round(2)
p.index=pd.to_datetime(p.index,format='%Y')
#for i in range(len(p)):
# print(i+1)
plt.plot(p['y'],'b-o')
plt.plot(p['y_pred'],'r-*')
plt.legend()
#plt.show()
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
plt.plot(data_1['y'],'b-o')
plt.plot(data_1['y_pred'],'r-*')
plt.legend()
# # 政府性基金收入采用GM11预测2006-2015年份收入,并和原值2006-2013比较
x0 = np.array([3152063, 2213050, 4050122, 5265142,5556619, 4772843,9463330])
f, a, b, x00, C, P = GM11(x0) # 得到预测函数f,可计算接下来预测值(和序号相关,按序预测)
len(x0)
p=pd.DataFrame(x0,index=range(2007,2014),columns=['y']) # 'y'要带上中括号
p.loc[2014]=None
p.loc[2015]=None
p['y_pred']=[f(i+1) for i in range(len(p))]
p=p.round(2)
p.index=pd.to_datetime(p.index,format='%Y')
#for i in range(len(p)):
# print(i+1)
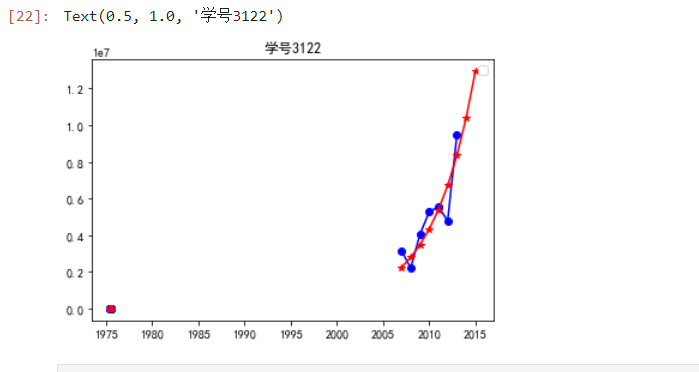
plt.plot(p['y'],'b-o')
plt.plot(p['y_pred'],'r-*')
plt.legend()
plt.title('学号3122')