【三维重建】运动恢复结构系统

代数法和分解法的局限性

因式分解法假定所有点都是可见的，所以下述场合不可用：

• 存在遮挡
• 建立对应点关系失败

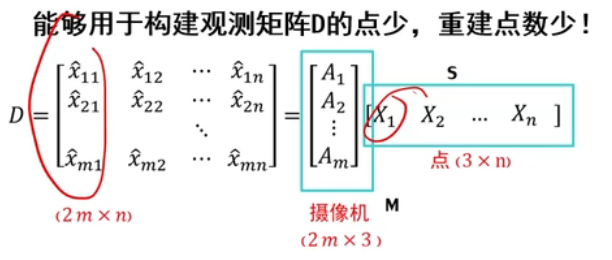
代数法应用于2视图重建

• 易出现误差累积！

捆绑调整（Bundle Adjustment）

• 恢复结构和运动的非线性方法

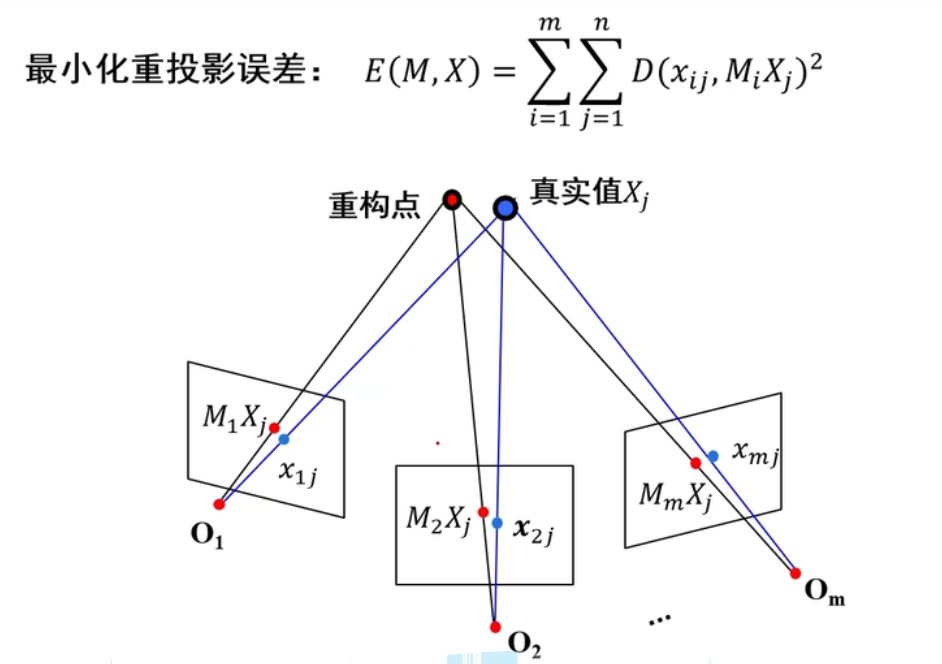
如上图所示，蓝色的是真实点，红色的是重构点，我们需要的是真实点和重构点之间的距离越小越好，也就是图中的那个公式(E即Error)，而公式中M和X是未知的，M是摄像机，X是三维点，我们的目标是优化表达式，使最终的目标最小。

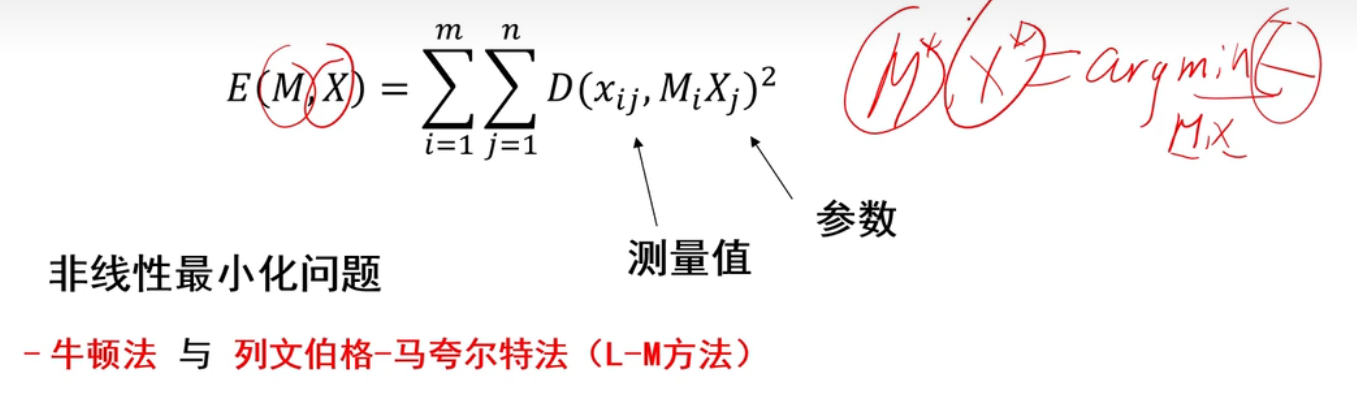
是E最小情况下的 $ M^* $ , $ X^* $ 就是我们所要求的。

优势:

• 同时处理大量视图
• 处理丢失的数据

局限性：

• 大量参数的最小化问题
• 需要良好的初始条件

实际操作：

• 常用作SFM的最后一步，分解或代数方法可作为优化问题的初始解

PNP问题：

PNP(Perspective-n-Point)问题：指通过世界中N个三维点坐标及其在图像中N个像点坐标，计算出相机或物体位姿的问题。

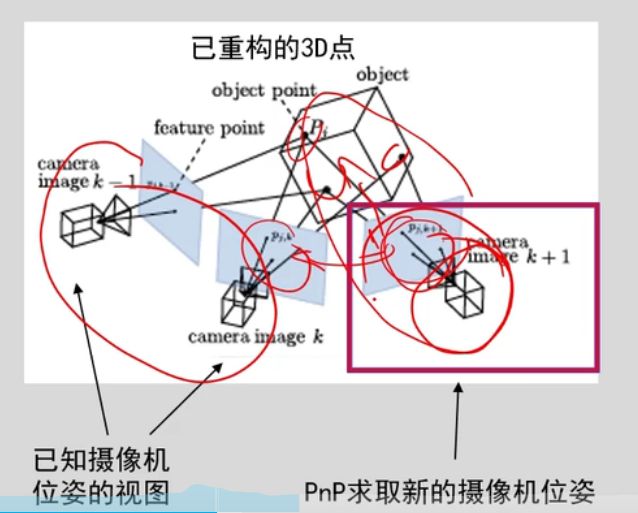
PNP问题就是已知camera image k+1图像上的点，求新的摄像机位姿，当然前提是需要知道三维点和camera image k+1上的对应关系，这种问题就是PNP。这样就可以求新相机的外参数，然后就可以求三角化了。

如果是已知camera image k - 1和camera image k图像上的对应点，然后求通过求解F->E->R、F，这种就是欧式结构恢复问题。

欧式结构恢复问题：

PNP问题之P3P

P3P：通过世界中3个三维点与图像中3个像点，计算摄像机的位姿。
已知：摄像机内参数K，像平面上a,b,c点的像素坐标以及其对应的三维点A,B,C在世界坐标系中的世界坐标。
求解：摄像机外参数R、T。
核心思路：

1. 求解A,B,C三点在当前摄像机坐标系下的坐标
2. 通过A,B,C在当前摄像机下的坐标以及其在世界坐标系下的坐标，估计摄像机相对于世界坐标系的旋转与平移。

步骤1：

步骤2：

步骤3：
结合OA、OB、OC线段长度可得A,B,C三点在摄像机坐标系下的坐标。

步骤4：
利用A、B、C在摄像机坐标系及世界坐标系的坐标，计算相机的运动R、T。

P3P缺点：只利用了三点信息，易受噪声干扰
其他算法：EPnP、UPnP，利用更多的信息、迭代优化，提升了估计的鲁棒性。

RANSAC

随机采样一致性（RANSAC，Random sample consensus）：一种适用于数据受到异常值污染的模型拟合方法。

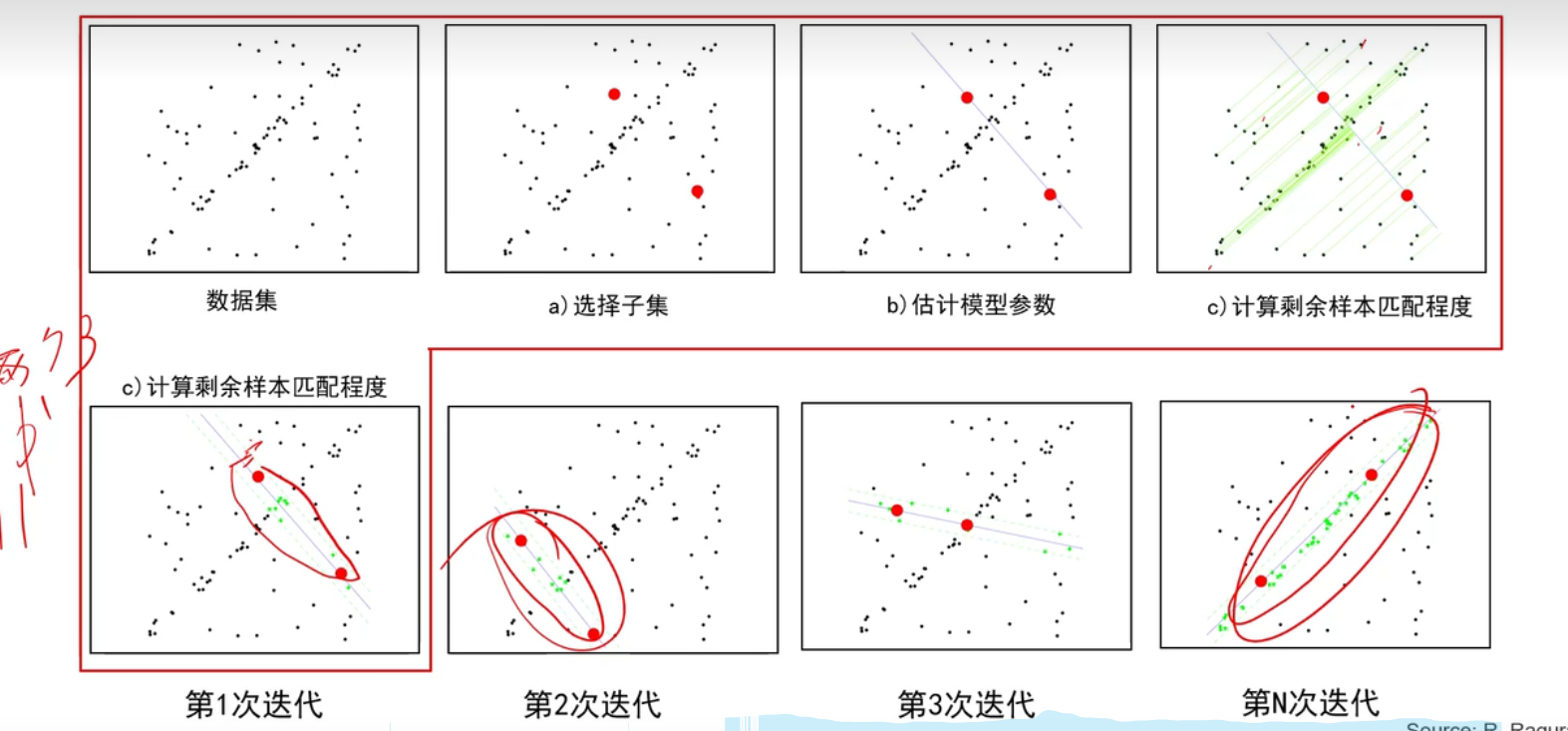
RANSAC思想：
随机采两个点(a)，两个点就能确定一条直线，把这两个点连起来(b),然后算所有点和这条线的距离(c)，然后设一个门限（当这条线低于这个门限时，就认为这些点都应该属于这条线，但是由于噪声没有在这个线上，而其他外面的点肯定不属于这条线上，在这个门限内的点叫做内点，门限外的点叫做外点），这个就叫做一次迭代（红框框起来的几个过程），这次迭代得到两个点，得到一条线，然后还得到一些内点个数（就是满足这条线的点的个数），然后给这条线打个分数，这个分数就是内点的个数。
第2次迭代又可以得到两个点，然后又可以得到一些内点个数，也就是这条线的分数。
这样迭代N次，总有一次能保证这条线的分数比较高，就把这条线找出来。

语言描述：
a）随机均匀采样获取模型求解所需的最小子集
b）适用该子集估计模型参数
c）计算剩余样本与当前模型的一致性，统计满足当前模型的点（内点）的个数，作为当前模型分数
d）以设定的次数重复a-c,最终输出分数最高的模型

参数设置：

• 初始点数量s：模型求解所需的最少的点的个数
• 距离门限t
• 采样次数N：选择采样次数N使得至少有一次采样为真实解的概率为p（例如：p=0.99）
• 必须匹配拟合模型的点数d：与内点数占比一致

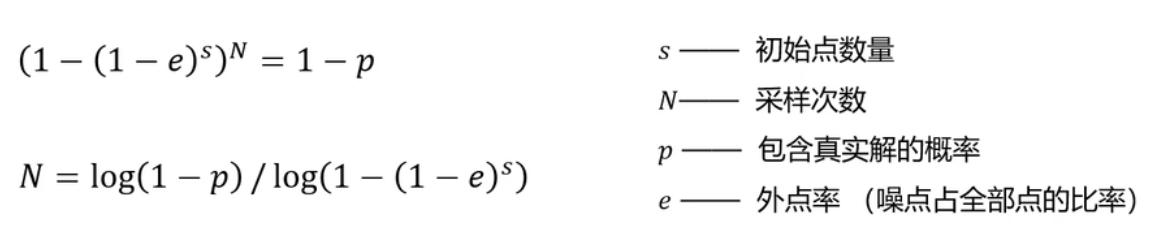
自适应迭代次数

• 外点率通常是未知的，按照最坏情况估计，比如50%；然后，根据计算结果自适应的调整外点比率，修正所需的总采样次数。
  

运动恢复结构（SFM）系统解析

单元技术：

• 单应矩阵
• 捆绑调整（BA）
• PnP与P3P
• RANSAC

单应矩阵

单应矩阵———空间平面在两个摄像机下的投影几何
描述的是两幅图像之间像点之间的对应关系，采集的点都是来自同一个平面的。

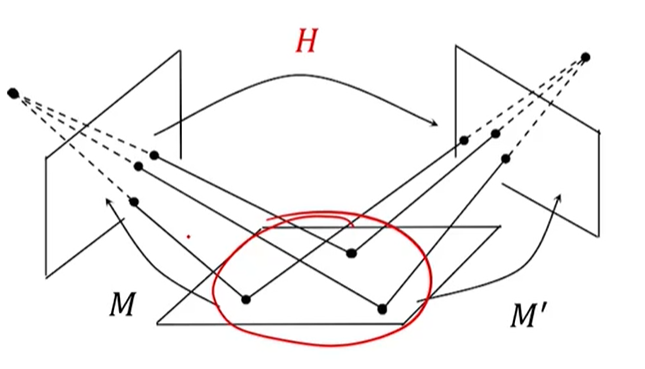
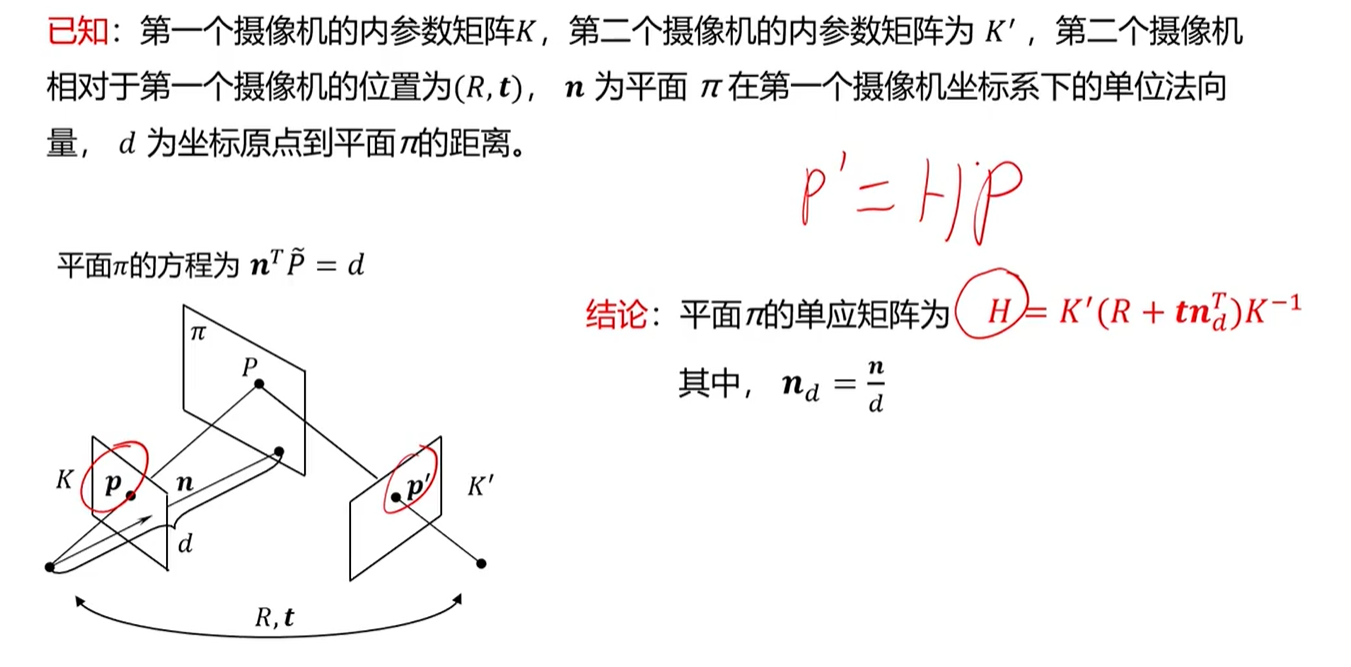
P和P'点的对应关系就是 $ p' = HP $,P和P'之间的关系就是H，（看红字结论那边）K和K'是两个相机的内参，R和t是两个相机之间的旋转和平移，唯一多了一个就是平面的法向量 $ n_d^T $,这样就在两个图像之间的像点之间建立了联系，然后我们也能求得H之后，

单应矩阵估计：

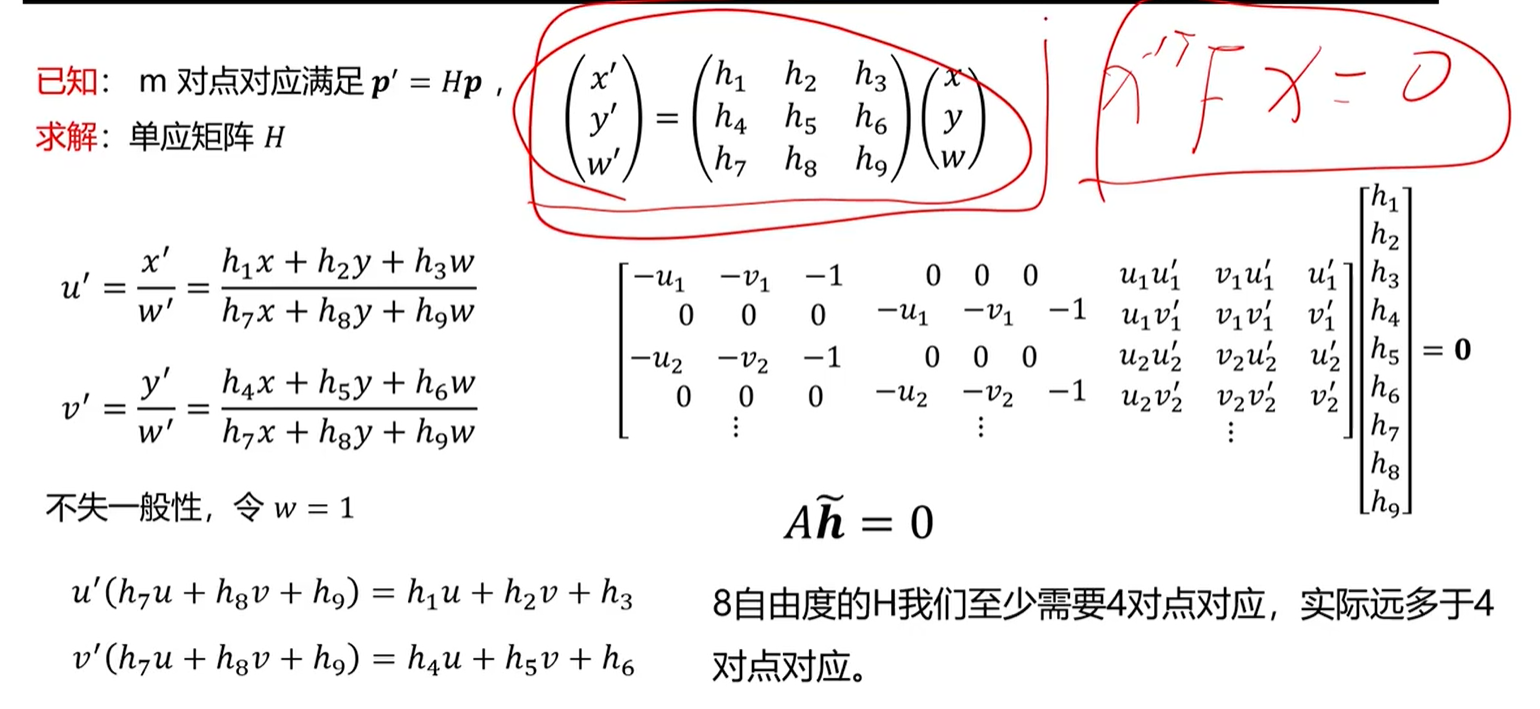
本质矩阵与单应矩阵区别

捆绑调整BA

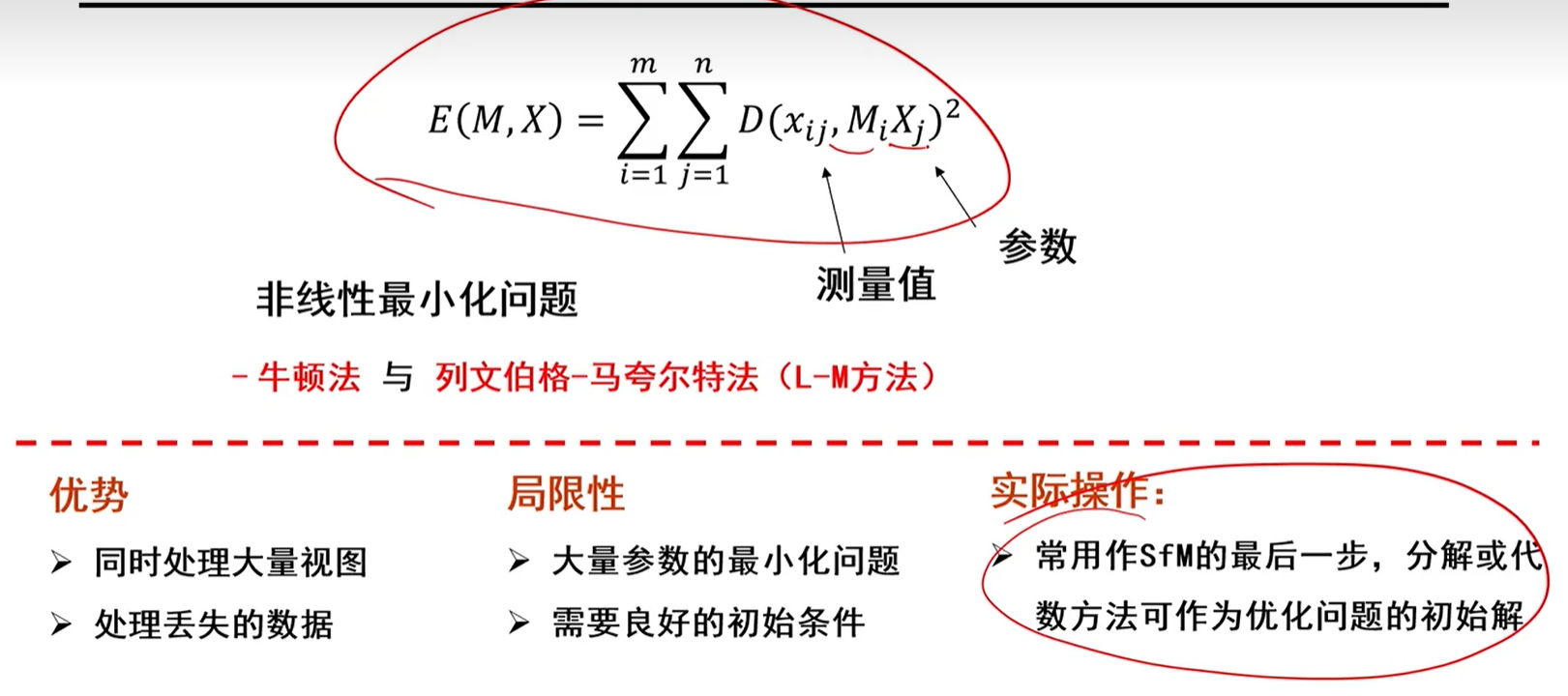
把摄像机和三维点重新进行调整一下，因为使用增量法已经构建了一个初始的条件，在这个基础上进行迭代，这样就会收敛很快，就能得到很好的结果，把累计偏差就分解到每个点上去了。
所有点和所有相机一起考虑，这样的稳定性只比两两的稳定性要高，因为所有的点和所有的误差都在这，一起优化，就是这样一个过程。

PnP与P3P

PnP解决的问题是：已知三维点和对应像素点的坐标，求相机的位姿。

RANSAC

RANSAC简单来说就是做模型拟合的

SFM系统问题描述（欧式重构）

已知：三维场景的m张图像以及每张图像对应的摄像机内参数矩阵$ K_i(i=1,...,m) $
求解：

• 三维场景结构，即三维场景点坐标\(X_j(j=1,...,n)\)
• m个摄像机的外参数\(R_i\)及\(T_i\)， \(i=1,...,m\)

---

SFM系统（两视图）

基于增量法的SFM系统——以OpenMVG为例（多视图）

欧式结构恢复（2视图）

特征提取

输入：图片
输出：具有尺度不变性的特征点（位置+每个特征的128维数据描述）

比如SIFT特征

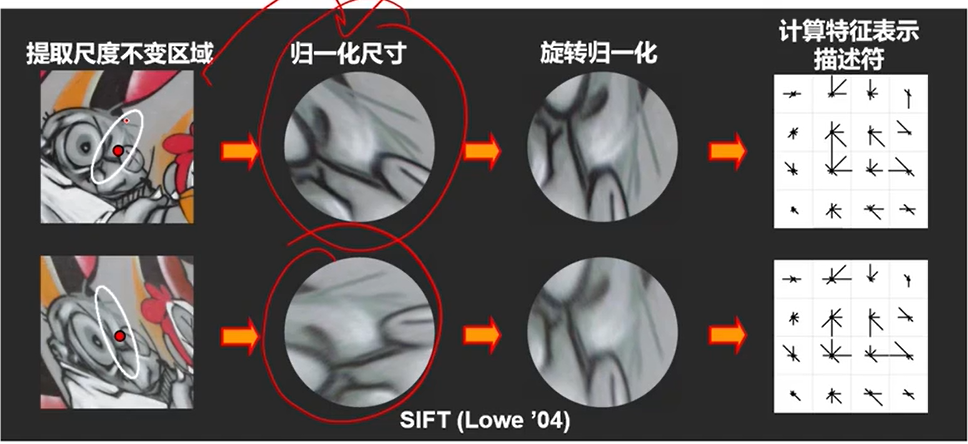
RANSAC估计基础矩阵

基于增量法的SFM系统（以OpenMVG为例）

系统流程：图像特征点提取与匹配 ——> 两视图重构初始点云 ——> 增加视图到系统实现多视图重构

一、预处理

预处理主要工作：

• 图像特征点提取与近邻匹配
• 基于RANSAC的基础矩阵或单应矩阵估计
  

二、增量法求解SFM

1、计算对应点的轨迹(Tracks)t

所以一般会计算每个点的轨迹并且把它存下来，这个点的轨迹是2，那个点的轨迹是3，在图像上的位置、图像的编号都存下来，这个存的就是所谓的tracks，接下来我们会用tracks。两张图像可以重构点，这个点的三维点可以重构出来，但是在我们系统里面不要，我们只要tracks为3的，tracks为2的不要，因为不稳定。Tracks就是一个点在多张图片里面的连接关系，

2、计算连接图G（结点代表图片，边代表其之间有足够的匹配点）

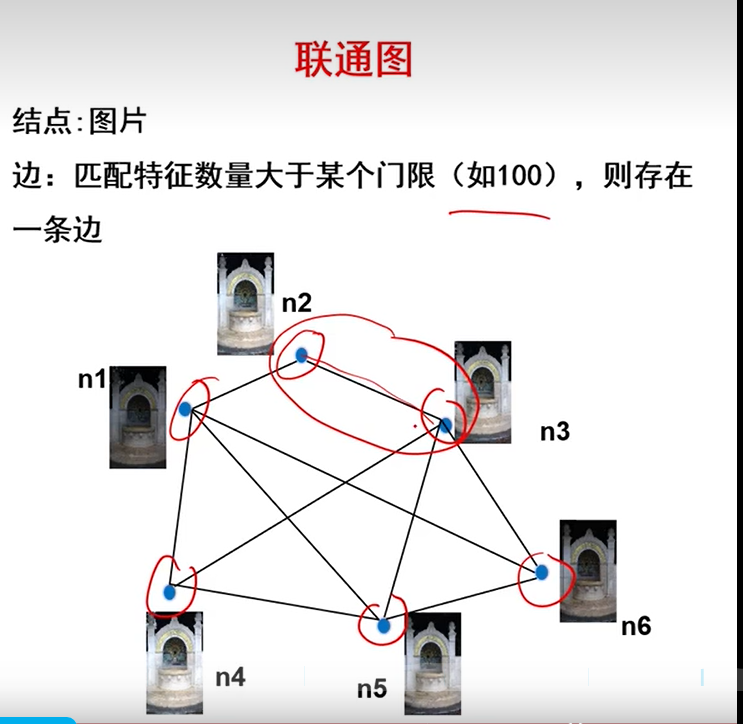
记录了图与图之间的矩阵，也记录他们之间的点匹配。

3、在G中选取一条边e
所有点对应点三角化时射线夹角中位数不大于60度不小于3度。

4、5、6 主要是两视图重构

8 增加视图到系统实现多视图重构