HMM学习笔记

HMM学习笔记

目录

• HMM学习笔记
  • 0 前言
  • 1 定义
    • 1.1 概念引入
    • 1.2 变量定义
    • 1.3 两个基本假设
    • 1.4 举例解释
    • 1.5 三个基本问题
  • 2 Evaluation Problem
    • 2.1 直接计算法
    • 2.2 前向算法
  • 3 Decoding Problem
  • 4 参考资料

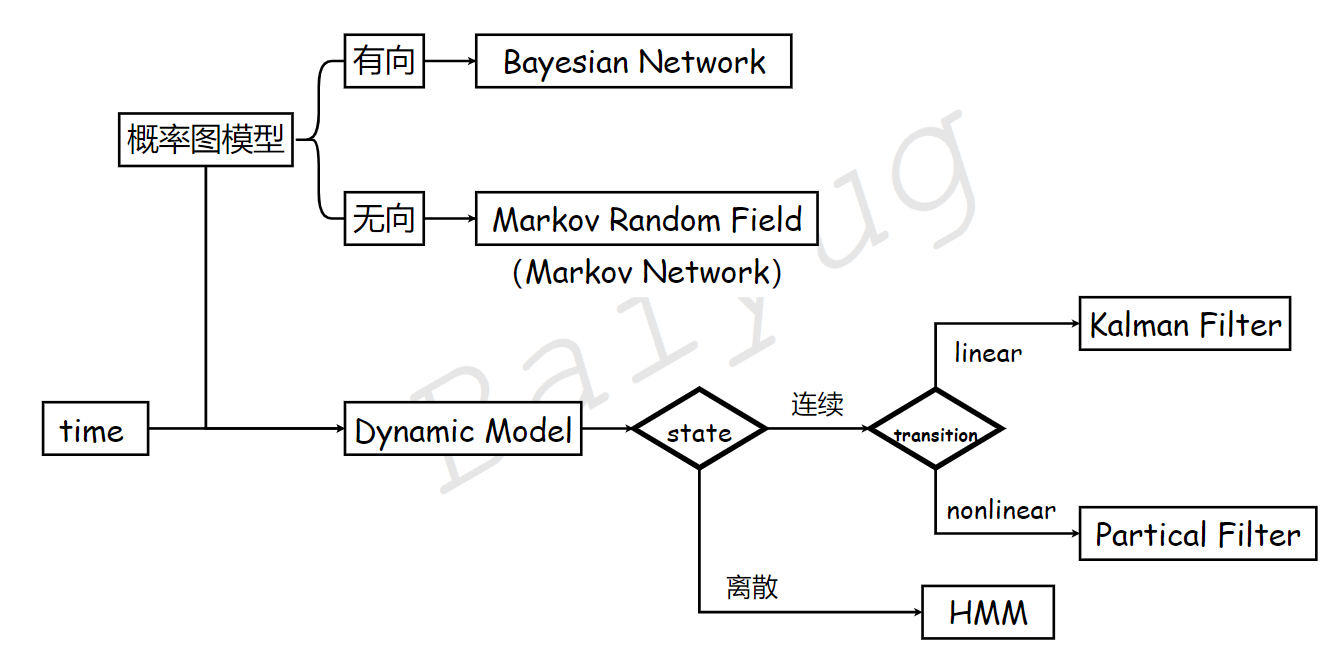
0 前言

隐马尔可夫模型（Hidden Markov Model,HMM）是一种经典的统计学模型，根本上属于传统机器学习中的概率图模型。学习该模型的前置知识为随机过程。

1 定义

1.1 概念引入

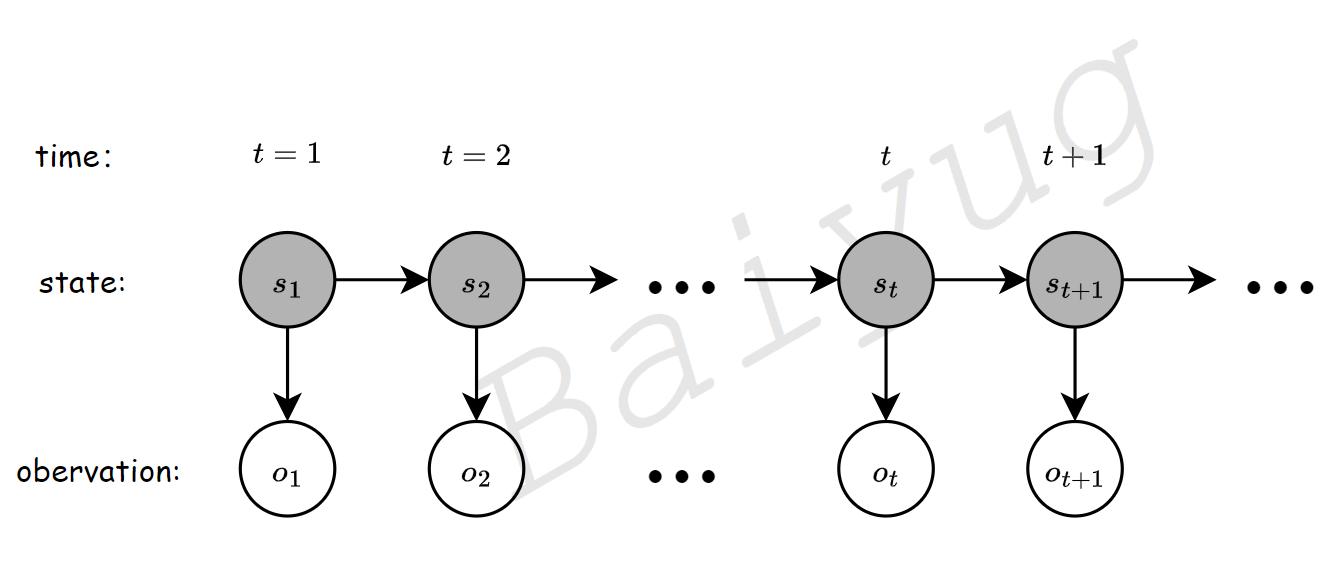
上图展示了隐马尔可夫链的基本元素和基本结构。隐马尔可夫的基本元素包含状态序列(state sequence)和观测序列(obervation sequence)，状态序列一般不可知，或者说被隐藏起来了，故名隐马尔可夫链，观测序列一般可知。从结构上可知，状态变量和观测变量会随着时间而变化。描述这个变化的过程需要引入状态转移概率矩阵A和观测概率矩阵B。

1.2 变量定义

设状态变量\(s_t\)的值域为\(Q=\{q_1,q_2,\cdots,q_t,\cdots,q_N\}\)，观测变量\(o_t\)的值域为\(V=\{v_1,v_2,\cdots,v_t,\cdots,v_M\}\)，\(N=length(Q)\)，\(M=length(V)\)。

设序列长度为\(T\)，则状态序列\(S=(s_1,s_2,\cdots,s_t,\cdots,s_T)\)，观测序列\(O=(o_1,o_2,\cdots,o_t,\cdots,o_T)\)。

定义状态转移概率矩阵

\[A=[a_{ij}]_{N\times N} \]

其中，\(a_{ij}=p(s_{t+1}=q_j|s_t=q_i),\qquad i=1,2,\cdots,N;j=1,2,\cdots,N\)。\(a_{ij}\)是在时刻\(t\)处于状态\(q_i\)条件下在时刻\(t+1\)转移到状态\(q_j\)的概率。

定义观测概率矩阵

\[B=[b_j(k)]_{N\times M} \]

其中，\(b_j(k)=P(o_t=v_k|s_t=q_j),\qquad k=1,2,\cdots,M;j=1,2,\cdots,N\)，\(b_j(k)\)是在时刻\(t\)处于状态\(q_j\)的条件下观测\(v_k\)的概率。

定义初始概率向量

\[\pi=[\pi_i]_{N\times 1} \]

其中，\(\pi_i=P(s_1=q_i),\qquad i=1,2,\cdots,N\)， \(\pi_i\)是时刻\(t=1\)处于状态 \(q_i\)的概率。

由此，可构建隐马尔可夫模型参数\(\lambda=(A,B,\pi)\)

1.3 两个基本假设

• (i)齐次马尔可夫性假设，即假设隐藏的马尔可夫链在任意时刻\(t\)的状态只依赖于前一时刻的状态，于其他时刻的状态及观测无关，也与时刻\(t\)无关。

  \[p(s_{t}|s_{t-1},\cdots,s_1,o_t,o_{t-1},\cdots,o_1)=p(s_{t}|s_{t-1}) \]

• (ii)观测独立性假设，即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态，与其他观测及状态无关。

  \[p(o_t|s_T,s_{T-1},\cdots,s_1,o_T,o_{T-1},\cdots,o_1)=p(o_t|s_t) \]

1.4 举例解释

假设现有{盒子1，盒子2，盒子3，盒子4}，每个盒子内含有若干数量不等的红球和白球。现在，观测者首先选择一个盒子，然后从该盒子里抽取一个球，获得该球的颜色，然后操作员会更换盒子，继续让观测者抽球。说明：盒子的更换规则观测者不知情。

那么，在这个例子中，观测者会获得一个关于小球颜色的序列，该序列就是观测序列；操作员依次更换盒子，操作员会得到一个关于盒子序号的序列，该序列就是对于观测者来讲就是状态序列，各个盒子中抽取红白球的概率会组成观测概率矩阵，盒子的更换方式会组成状态转移概率矩阵，观测者选择第一个盒子的概率分布称为初始状态概率向量。

详细例子见《统计学习方法》，李航，清华大学出版社，P173

1.5 三个基本问题

• Evaluation：已知\(O,\lambda\)，求解\(p(O|\lambda)\)；

• Learning：已知\(O\)，求\(\lambda\)，使\(\lambda_{MLE}=\mathop{argmax}\limits_{\lambda}p(O|\lambda)\)

• Decoding：已知\(O,\lambda\)，求\(S\)，使\(\hat{S}=\mathop{argmax}\limits_{S}p(S|O,\lambda)\)

2 Evaluation Problem

2.1 直接计算法

\[\begin{aligned} p(O|\lambda) &= \sum\limits_{S}p(S,O|\lambda) \\ &= \sum\limits_{S}p(O|S,\lambda)p(S|\lambda) \end{aligned} \]

注：
边缘概率可以展开为联合概率的和；
联合概率可以展开为含有条件概率的形式；如\(P(AB)=P(A|B)P(B)\)

根据基本假设(i)，可得

\[\begin{aligned} p(S|\lambda)&= p(s_1,s_2,\cdots,s_t|\lambda)\\ &= p(s_t|s_1,s_2,\cdots,s_{t-1},\lambda)p(s_1,s_2,\cdots,s_{t-1}|\lambda)\\ &= a_{s_{t-1}s_t} a_{s_{t-2}s_{t-1}} \cdots a_{s_1s_2}\\ &= \pi_{s_1}\prod\limits_{t=2}^Ta_{s_{t-1},s_t} \end{aligned} \]

注：其中，\(a_{s_{t-1},s_t}\) 表示从状态\(s_{t-1}\)到状态\(s_t\)的转移概率，为了和1.2中的变量a_{ij}相对应，可以令\(i=locate(s_{t-1})\)，\(j=locate(s_t)\)，对应\(s_{t-1}\)和\(s_t\)在\(Q\)(定义见1.2)中的位置序号，则\(a_{s_{t-1},s_t}\)可以用\(a_{ij}\)表示，上式为了表述清晰，便直接使用状态变量代替了位置序号，与定义中的公式表达略有不同。

根据基本假设(ii)，对于状态序列\(S=(s_1,s_2,\cdots,s_t,\cdots,s_T)\)，有

\[p(O|S,\lambda)=\prod\limits_{t=1}^Tb_{s_t}(o_t) \]

注：上式与\(a_{ij}\)类似，使用状态变量\(s_t\)表示状态变量在\(Q\)中的位置序号，使用观测变量\(o_t\)表示观测变量在\(V\)(定义见1.2)中的位置序号。

于是有

\[p(O|\lambda)=\sum\limits_{S}\pi_{s_1}\prod\limits_{t=2}^Ta_{s_{t-1},s_t}\prod\limits_{t=1}^Tb_{s_t}(o_t) \]

对上述\(\sum\limits_{S}\)做解释：这里的意思是对后面的含有\(s_1,s_2,\cdots,s_T\)这些\(T\)个随机变量分别求均值再求和，即对状态变量求T次均值，每个状态变量都有\(N\)个取值，也就是说，计算上式需要进行\(N^T\)个均值计算再求和，计算时间复杂度为\(O(N^T)\)。随着\(T\)的增加，时间计算复杂度指数级增长。

2.2 前向算法

给定\(\lambda\)，\(O=(o_1,o_2,\cdots,o_t)\)，定义：到时刻\(t\)观测序列为\(o_1,o_2,\cdots,o_t\)且状态为\(q_i\)的概率为前向概率，记为

\[\alpha_t(i)=p(o_1,o_2,\cdots,o_t,s_t=q_i|\lambda) \]

所以，

\[p(O|\lambda)=\sum\limits_{i=1}^Np(O,s_t=q_i|\lambda)=\sum\limits_{i=1}^N\alpha_t(i) \]

因此，欲求时刻t的\(p(O|\lambda)\)，即求 \(\alpha_t(i)\)。可以通过递归的思想求解\(\alpha_t(i)\)

\[\begin{aligned} \alpha_{t}(j)&=p(o_1,o_2,\cdots,o_{t},s_{t}=q_j|\lambda)\\ &=\sum\limits_{i=1}^Np(o_1,o_2,\cdots,o_{t},s_{t-1}=q_i,s_t=q_j|\lambda)\\ &=\sum\limits_{i=1}^Np(o_{t}|o_1,o_2,\cdots,s_{t-1}=q_i,s_{t}=q_j|\lambda)p(o_1,\cdots,o_{t-1},s_{t-1}=q_i,s_{t}=q_j|\lambda) \\ &=\sum\limits_{i=1}^Np(o_{t}|s_{t}=q_j)p(o_1,\cdots,o_t,s_{t-1}=q_i,s_{t}=q_j|\lambda) \\ &=\sum\limits_{i=1}^Np(o_{t}|s_{t}=q_j)p(s_{t}=q_j|o_1,\cdots,o_t,s_{t-1}=q_i,\lambda)p(o_1,\cdots,o_t,s_{t-1}=q_i|\lambda) \\ &=\sum\limits_{i=1}^Np(o_{t}|s_{t}=q_j)p(s_{t}=q_j|s_{t-1}=q_i)p(o_1,\cdots,o_t,s_{t-1}=q_i|\lambda) \\ &=\sum\limits_{i=1}^Nb_{j}(o_t)a_{ij}\alpha_{t-1}(i) \end{aligned} \]

可以看出来，上式依旧是使用了2.1使用过技巧

• 将联合概率拆解为条件概率及其条件的概率的乘积
• 利用基本假设(i)(ii)

因此，给定\(\lambda=(A,B,\pi), O=(o_1,o_2,\cdots,o_T)\)， 可得\(\alpha_t(i)\) 的初始条件 \(\alpha_1(i)\)

\[\alpha_1(i)=\pi_ib_i(o_1) \]

然后可以利用推导出的递归表达式计算出\(\alpha_t(1),\alpha_t(2), \cdots,\alpha_t(T)\)，然后求和即可得到\(p(O|\lambda)\)。在每个递归式中，需要计算\(N\)个\(\alpha_{t-1}(i),\{i=1,2,\cdots,N\}\)，获得\(N\)个\(\alpha_{t}(i),\{i=1,2,\cdots,N\}\)，则每个递归式的时间复杂度为\(O(N^2)\)，又观测序列的长度为\(T\)，即需要进行T次递归，则该算法的时间复杂度为\(O(N^2T)\)。

3 Decoding Problem

decoding 问题就是根据观测序列求解最有可能的状态序列。

该问题的求解主要涉及到Viterbi Algorithm（维特比算法）。维特比算法是一种动态规划算法。它用于寻找最有可能产生观测事件序列的维特比路径——隐含状态序列。

定义：观测序列为\(o_1,o_2,\cdots,o_t\)，模型参数为\(\lambda\)，到时刻\(t\)，状态变量\(s_t\)为\(q_i\)的概率最大，概率大小记为\(\delta_t(i)\)。

\[\delta_{t}(i)=\max\limits_{s_1,\cdots,s_{t-1}}p(o_1,\cdots,o_t,s_1,\cdots,s_{t-1},s_t=q_i|\lambda) \]

相应的，可以推出

\[\delta_{t+1}(j)=\max\limits_{1\le i\le N}[\delta_t(i)a_{ij}]b_j(o_{t+1}) \]

定义在时刻\(t+1\)状态为\(j\)的所有单个路径\((j_1,j_2,\cdots,j_t,j_{t+1})\)中概率最大的路径的第\(t+1\)个节点为

\[\psi_{t+1}(j)=\mathop{argmax}\limits_{1\le i\le N}[\delta_t(i)a_{ij}] \]

代码示例

物理背景同1.4

clc
clear 
close all

A = [0.5 0.2 0.3;
     0.3 0.5 0.2;
     0.2 0.3 0.5];
B = [0.5 0.5;
     0.4 0.6;
     0.7 0.3];
PI = [0.2; 0.4; 0.4];

lambda = {A, B, PI};

%红-1 白-2
O = [1 2 1];
%代码中的输入观测序列和输出状态序列需进行合理的数学编码，例如上述O代表{红，白，红}，输出状态序列同理
my_viterbi(lambda, O)

function S_decode = my_viterbi(lambda, O)
    A = lambda{1, 1};
    B = lambda{1, 2};
    PI = lambda{1, 3};
    numO = length(O);
    S_decode = zeros(1, numO);

    % initialize
    N = length(PI);% number of states
    Psi = zeros(N, numO);
    Delta = zeros(N, numO);
    for i = 1:N
        Delta(i, 1) = PI(i) * B(i, O(1));
    end

    % recursive
    for k = 1:numO-1
        for i = 1:N
            temp = zeros(N,1);
            for j = 1:N
                temp(j) = Delta(j, k)*A(j,i);
            end
            [temp_max, max_index] = max(temp);
            Delta(i, k+1) = temp_max*B(i, O(k+1));
            Psi(i, k+1) = max_index;
        end
    end

    % end
    [temp_max, max_index] = max(Delta(:, end));
    P_decode_path = temp_max;
    tail_decode_point = max_index;

    % path traceback
    S_decode(numO) = tail_decode_point;
    for k = numO-1:-1:1
        S_decode(k) = Psi(S_decode(k+1), k+1);
    end
end

4 参考资料

[1] b站机器学习白板推导系列[DB/OL]
[2] 统计学习方法[M].李航.清华大学出版社.2011.