背包九讲(7)

背包九讲(7)

有依赖的背包问题

有 N 个物品和一个容量是 V的背包。

物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。

如下图所示：

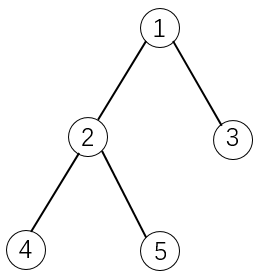
如果选择物品5，则必须选择物品1和2。这是因为2是5的父节点，1是2的父节点。

每件物品的编号是 ii，体积是 vi，价值是 wi，依赖的父节点编号是 pi。物品的下标范围是 1…N。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式

第一行有两个整数 N，V，用空格隔开，分别表示物品个数和背包容量。

接下来有 N 行数据，每行数据表示一个物品。
第 ii 行有三个整数 vi,wi,pi，用空格隔开，分别表示物品的体积、价值和依赖的物品编号。
如果 pi=−1，表示根节点。 数据保证所有物品构成一棵树。

输出格式

输出一个整数，表示最大价值。

数据范围

1≤N,V≤100
1≤vi,wi≤100

父节点编号范围：

• 内部结点：1≤pi≤N
• 根节点 pi=−1

输入样例

5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2

输出样例：

11

没看懂，暂时放上别人的解答，以后再考虑

AcWing 10. 有依赖的背包问题（思路不同于dxc，但是个人感觉更好理解） - AcWing

#include<iostream>
#include<vector>
using namespace std;
int f[110][110];//f[x][v]表达选择以x为子树的物品，在容量不超过v时所获得的最大价值
vector<int> g[110];
int v[110],w[110];
int n,m,root;

int dfs(int x)
{
    for(int i=v[x];i<=m;i++) f[x][i]=w[x];//点x必须选，所以初始化f[x][v[x] ~ m]= w[x]
    for(int i=0;i<g[x].size();i++)
    {
        int y=g[x][i];
        dfs(y);
        for(int j=m;j>=v[x];j--)//j的范围为v[x]~m, 小于v[x]无法选择以x为子树的物品
        {
            for(int k=0;k<=j-v[x];k++)//分给子树y的空间不能大于j-v[x],不然都无法选根物品x
            {
                f[x][j]=max(f[x][j],f[x][j-k]+f[y][k]);
            }
        }
    }
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        int fa;
        cin>>v[i]>>w[i]>>fa;
        if(fa==-1)
            root=i;
        else
            g[fa].push_back(i);
    }
    dfs(root);
    cout<<f[root][m];
    return 0;
}