机器学习二 -- 决策树学习
决策树学习
从今天开始,坚持每天学习一个机器学习的新知识,加油!
决策树学习是应用最广的归纳推理算法之一,是一种逼近离散值目标函数的方法,在这种方法中学习到的函数被表示为一颗决策树。
决策树表示法
决策树通过把实例从根结点排列到某个叶子结点来分类实例,叶子结点即为实例所属的分类。树上的每一个结点指定了对实例的某个属性的测试,并且该结点的每一个后继分支对应于该属性的一个可能值。分类实例的方法是从这棵树的根节点开始,册数这个结点指定的属性,然后按照给定实例的该属性对应的树枝向下移动,然后这个过程再以新结点为根的子树上重复。
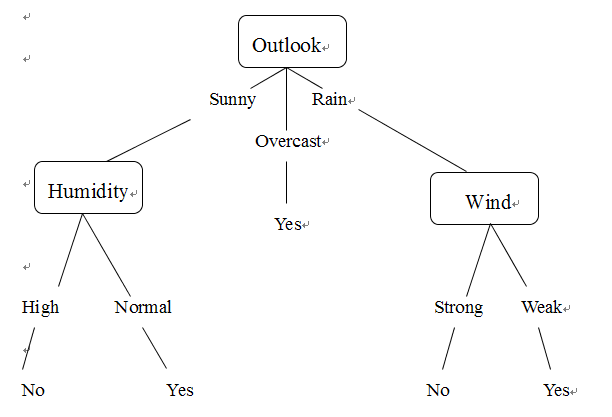
上图画出了一颗典型的学习到的决策树,这颗决策树根据天气情况分类“星期六上午是否适合打网球”。貌似很多机器学习和数据挖掘的书籍提到这个决策树的时候都是说的这个例子,汗!不过呢,我们还可以根据这颗决策树写出对应的表达式:
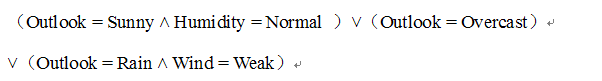
决策树学习的适用问题
- 实例是由“属性-值”对(pair)表示的
- 目标函数具有离散的输出值
- 可能需要析取的描述
- 训练数据可以包含错误
- 训练数据可以包含缺少属性值的实例
决策树学习的应用列举
- 根据疾病分类患者
- 根据起因分类设备故障
- 根据拖欠支付的可能性分类贷款申请
决策树学习的算法ID3
基本的ID3算法通过自顶向下构造决策树来进行学习。构造过程是从“哪一个属性将从树的根结点被测试?”这个问题开始的。我们使用统计测试来确定每一个实例属性单独分类训练样例的能力。分类能力最好的属性(即信息增益最大的属性)被选作树的根结点的测试。然后为根结点属性的每个可能值产生一个分支,并把训练样例排列到适当的分支之下。然后重复整个过程,用每个分支结点关联的训练样例来选取在该点被测试的最佳属性。这形成了对合格决策树的贪婪搜索,也就是算法从不回溯重新考虑以前的选择。
熵:表示了任意样例集的纯度。
假定S为训练集,S的目标属性C有m个可能的类标号值,C={C1,C2,C3…Cm},每个类标号值相应的概率为p1,p2,p3…pm。那么训练集S的信息熵定义为:Entropy(S)=Entropy(p1,p2,,,,pm)=-(p1*log2(p1)+p2*log2(p2)+pm*log2(pm));
信息增益:一个属性的信息增益就是由于使用这个属性分割样例而导致的期望熵降低。
假设训练集为S,并用属性A来划分S,那么属性A的信息增益Gain(S,A)为训练集S的熵减去按属性A划分S后的子集的熵,即Gain(S,A) = Entropy(S) - Entropy_A(S)。
Entropy_A(S)=abs(Si)/abs(S)Entropy(Si)(Si表示描述属性A的离散值的集合,abs(Si)表示属性A当前这个值的个数)
ID3 算法的优势和不足
它是关于现有属性的有限离散值函数的一个完整空间。但是当遍历决策树空间时,ID3 仅维护单一的当前假设,这样就失去了表示所有一致假设带来的优势,而且ID3 算法在搜索中不进行回溯,每当在树的某一层次选择了一个属性进行测试,它不会再回溯重新考虑这个选择,所以它易受无回溯的爬山搜索中的常见风险影响:收敛到局部最优的答案,而不是全局最优的。
决策树学习的归纳偏置
如果给定一个训练样例的集合,那么通常有很多决策树与这些样例一致。所以,要描述ID3 算法的归纳偏置,应该找到它从所有一致的假设中选择一个的根据。ID3从这些决策树中会选择哪一个呢?它会选择在使用简答到复杂的爬山算法遍历可能的树空间时遇到的第一个可接受的树。总结的说,ID3归纳偏置的搜索策略为:较短的树比较长的树优先;那些信息增益高的属性更靠近根结点的树优先。
为什么短的假设优先?
假设物理学家优先选择行星运动简单的解释,而不用复杂的解释,为什么?一种解释是短假设的数量少于长假设的数量,所以找到一个短的但同时与训练数据拟合的假设的可能性较小。相反,常常有很多非常复杂的假设拟合当前的训练数据,但却无法正确地泛化到后来的数据。比如考虑决策树假设,500个结点的决策树比5个结点的决策树多得多,如果给定一个20个训练样例的集合,可以预期能够找到很多500个结点的决策树与训练数据一致,而如果一个5个结点的决策树也可以完美的拟合这些数据当然是出乎意料的。所以我们会相信5个结点的树不太可能是统计巧合,因而优先选择这个5个结点的决策树的假设,而不选择500个结点的。
处理决策树学习的常见问题
避免过度拟合数据
对于一个假设,当存在其他的假设对训练数据样例的拟合比它差,但事实上在实例的整个分布中表现得却更好时,我们说这个假设过度拟合。
避免决策树学习中的过度拟合的方法被分为两类:
- 及早停止树增长,在ID3算法完美分类训练数据之前就停止树增长。
- 后修剪法:即允许树过度拟合数据,然后对这个树进行后修剪。
在实践中证实第二种方法后修剪更加成功的实施准则:
1:使用与训练样例截然不同的一套分离的样例,来评估通过后修剪方法从树上修剪结点的效用。
2:使用所有可用数据进行训练,但是进行统计测试来估计扩展(或修剪)一个特定的结点是否有可能改善在训练集合外的实例上的性能。
3:使用一个明确的标准来衡量训练样例和决策树的复杂度,当这个编码的长度最小时停止树增长。
合并连续值的属性
我们最初的ID3定义被限制为取离散值的属性。所以,我们可以先把连续值属性的值域分割为离散的区间集合。例如,对于连续值的属性A,算法可以动态的创建一个新的布尔属性Ac,如果A<c,那么Ac为真,否则为假。这样,就把连续值的属性的值离散化了。
属性选择的其他度量标准
有一些极端的例子里,采取信息增益来作为选择树的结点的优先性,有时这棵树虽然可以理想的分类训练数据,但是对于实例的数据的性能非常差,不是一个很好的预测器。所以我们选择了新的度量标准:增益比率。增益比率的计算方法先略过,这个我在后面的总结里会详细的讲解到。
处理缺少属性值的训练样例
- 赋给属性A决策结点n的训练样例中该属性的最常见值。
- 为属性A的每个可能值赋予一个概率。
处理不同代价的属性
在某些学习任务中,实例的属性可能与代价相关。例如,在学习分类疾病时,我们可能以这些属性来描述患者:体温、活组织切片检查、脉搏、血液化验结果等,这些属性在代价方面差别非常大。对于这样的任务,我们将优先选择尽可能使用低代价属性的决策树,通过引入一个代价项到属性选择度量中,我们可以用信息增益除以属性的代价,这样我们就可以使低代价的属性会被优先选择。仅当需要产生可靠的分类时我们才依赖高代价属性。



