XDRender_HLSL_LightMAtrix. 空间变换2-灯光空间(ViewMatrix,ProjectionMatrix)
XDRender_HLSL_LightMAtrix. 空间变换2-灯光空间(ViewMatrix,ProjectionMatrix)
@Author:白袍小道

前言
我们很多的渲染Feature和技术, 都需要获取灯光空间下的信息.
这里就避免不了, 我们需要构建合适的灯光的
1、ViewMatrix
2、ProjectionMatrix
3、额外相关的参数
另外, 为何不直接使用已经封装好的.这有两个原因:
1、我们后面其他地方也需要, 如果没有合适的暴露函数情况下就坑了
2、对推导熟悉, 也能让我们用起来更加安心和注意.
正文
由于这里采用列主序, 故而是左乘矩阵的方式.
理论
一、行主序和列主序
关于左乘和右乘的区别,请参考空间变换1, 或者其他相关资料.
行主序:mij
列主序:mji
二、ViewMatrix
假设相机坐标系的基: U-Up, V-Forward, N
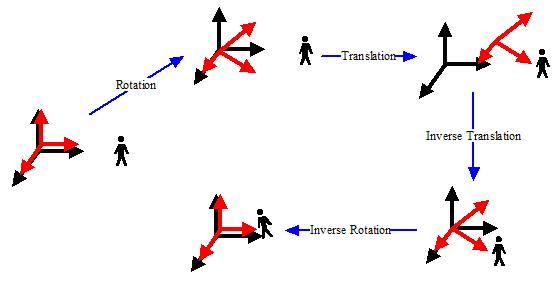
相机的ViewMatrix可以用两个属性来描述——朝向和位置.
Inverse Translation: 位置的逆变换
Inverse Rotation: 旋转的逆变换
假设相机本身的变化: 先旋转-然后再移动, 就先简单描述下推导.
推导过程
C=TR
那么相机的
(C)Inver = (TR)Inver
(C)Inver = (R)Inver * (T)Inver
这样我们先做简单的位置的逆变换
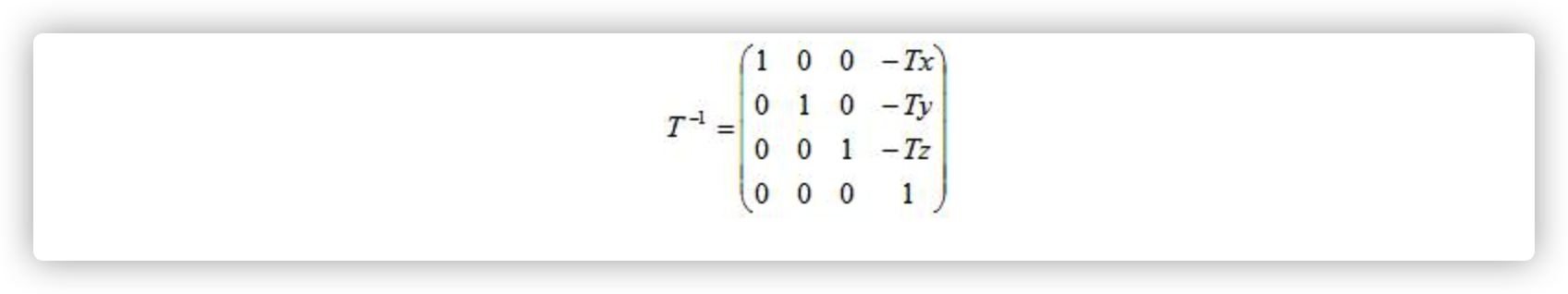
假设一个世界空间下的点V, 经过这个变化将V变化到了V‘,其中 V’ 为相机下的点
接下来我们处理R
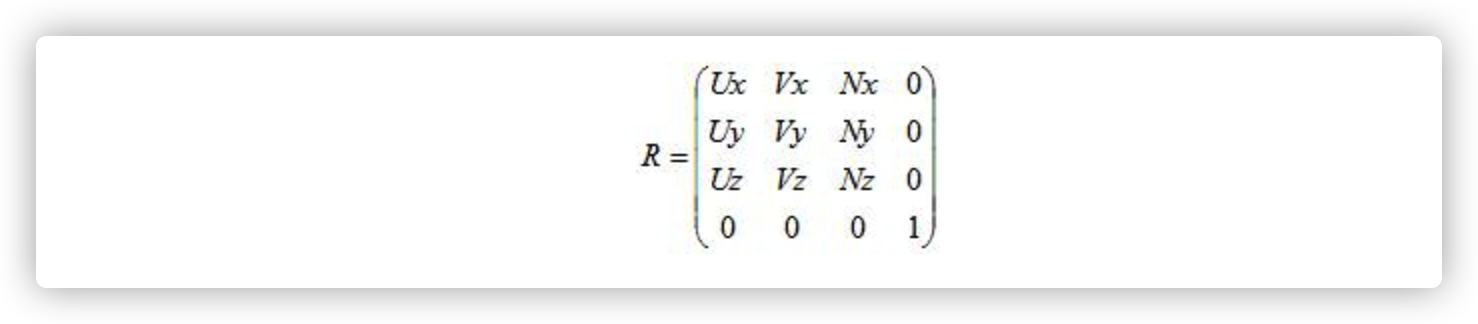
我们先用世界坐标系”Y轴基向量”,通过 look和eye点 得到Z轴基向量
叉乘得X轴基向量,但是我们知道Y基向量,不是真正的基向量。重新叉乘得到真正的Y轴基向量。
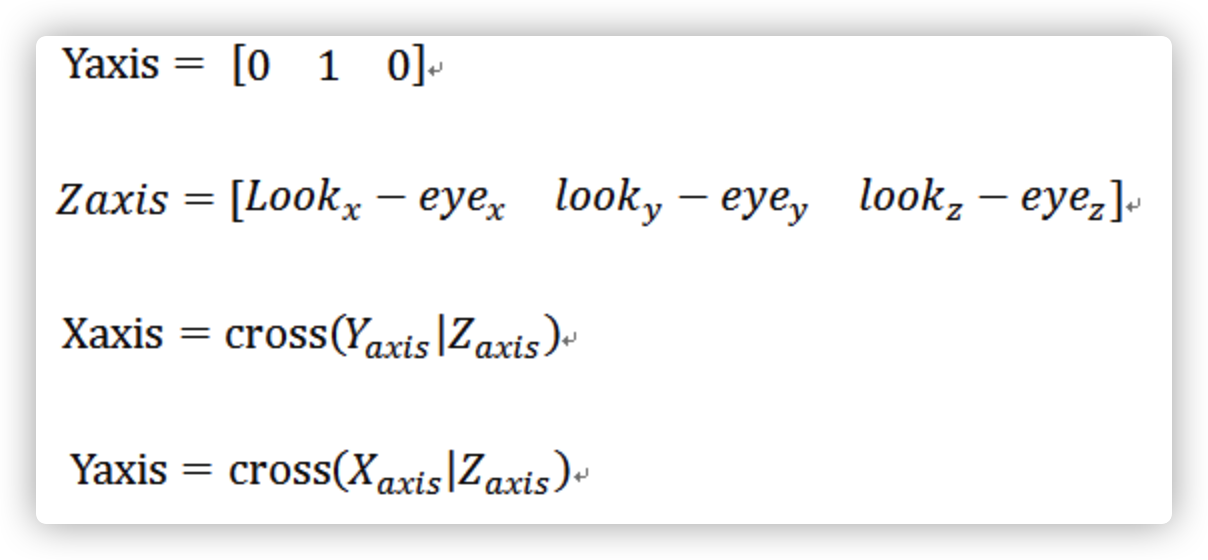
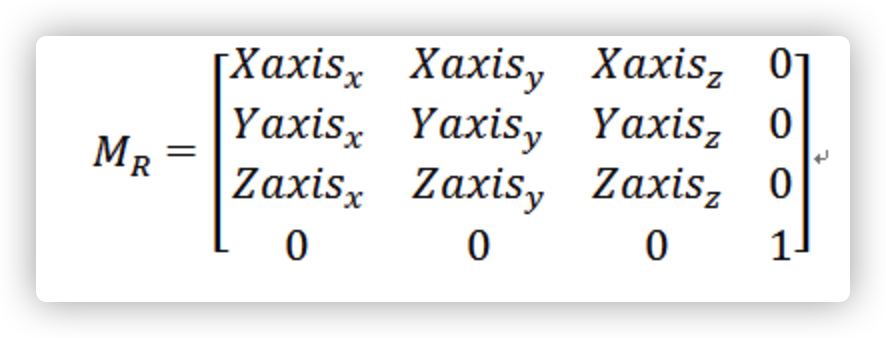
现在我们有了T , 和R, 接下来就是矩阵组合了. 注意下这里是列主序,左乘方式
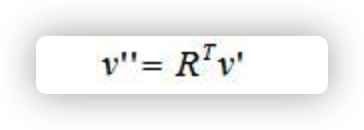
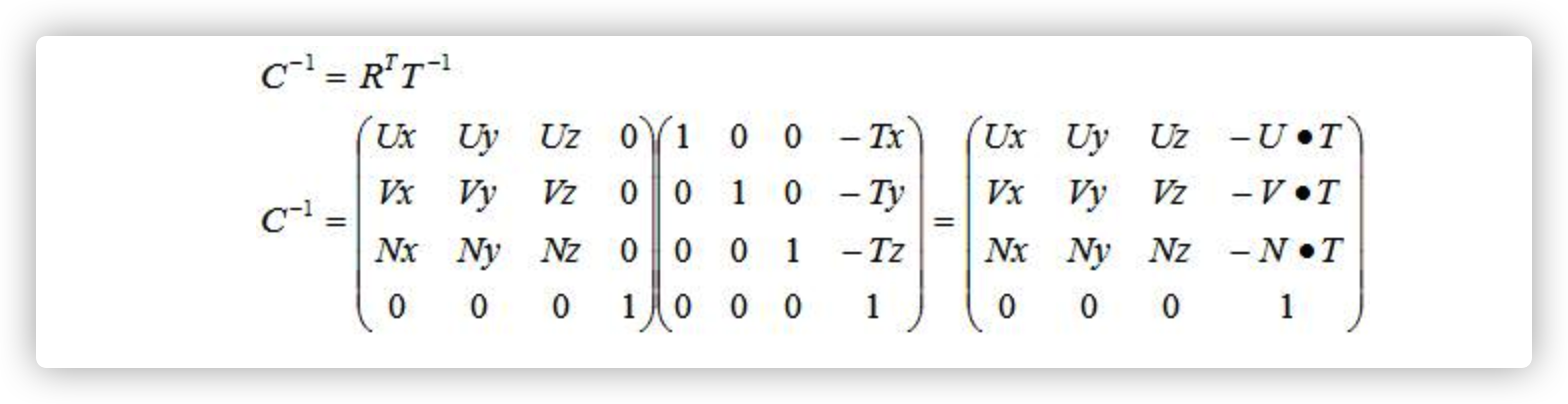
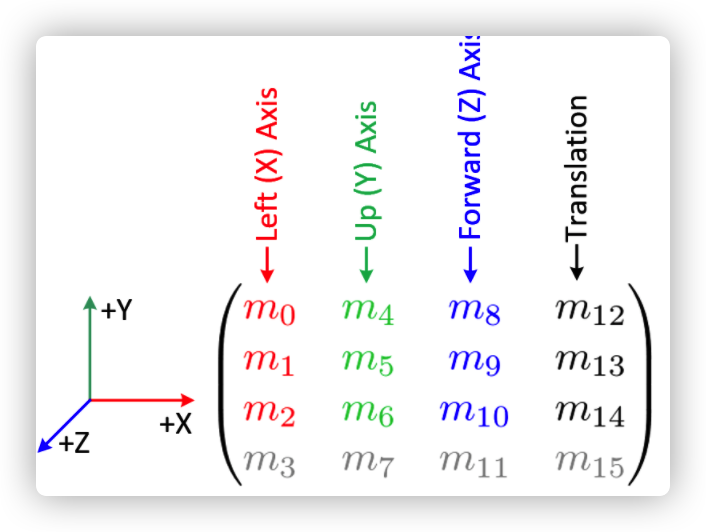
额外一点
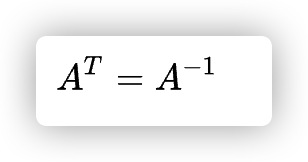
三、ProjectionMatrix
这个是比较麻烦的部分, 我们尝试分析一下.
1、简单正交投影(线性关系)
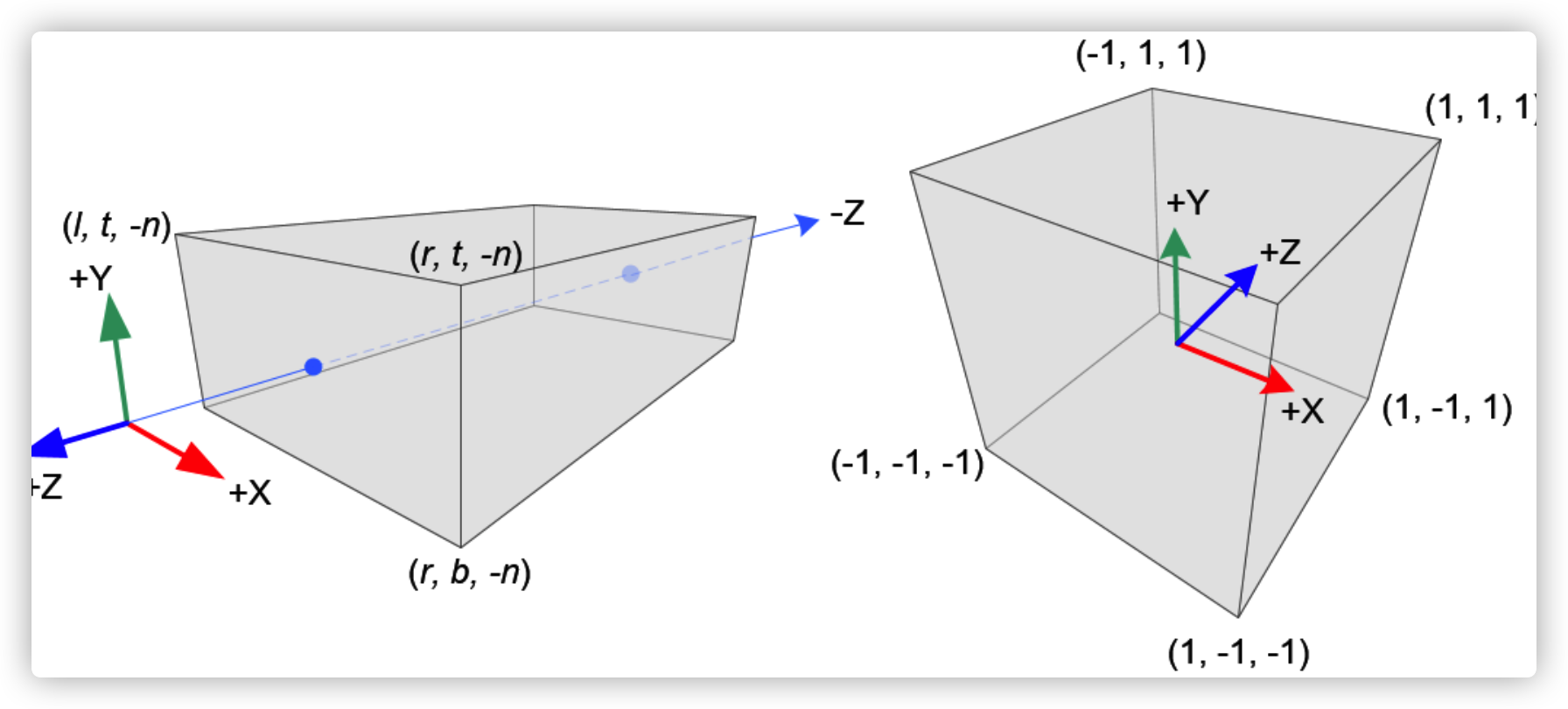
视野空间中所有xe、ye和ze组件线性映射到NDC。我们只需要将一个矩形体积缩放成一个立方体,然后将它移动到原点。让我们使用线性关系找出GL_PROJECTION的元素。

限于篇幅直接参考:http://www.songho.ca/opengl/gl_projectionmatrix.html
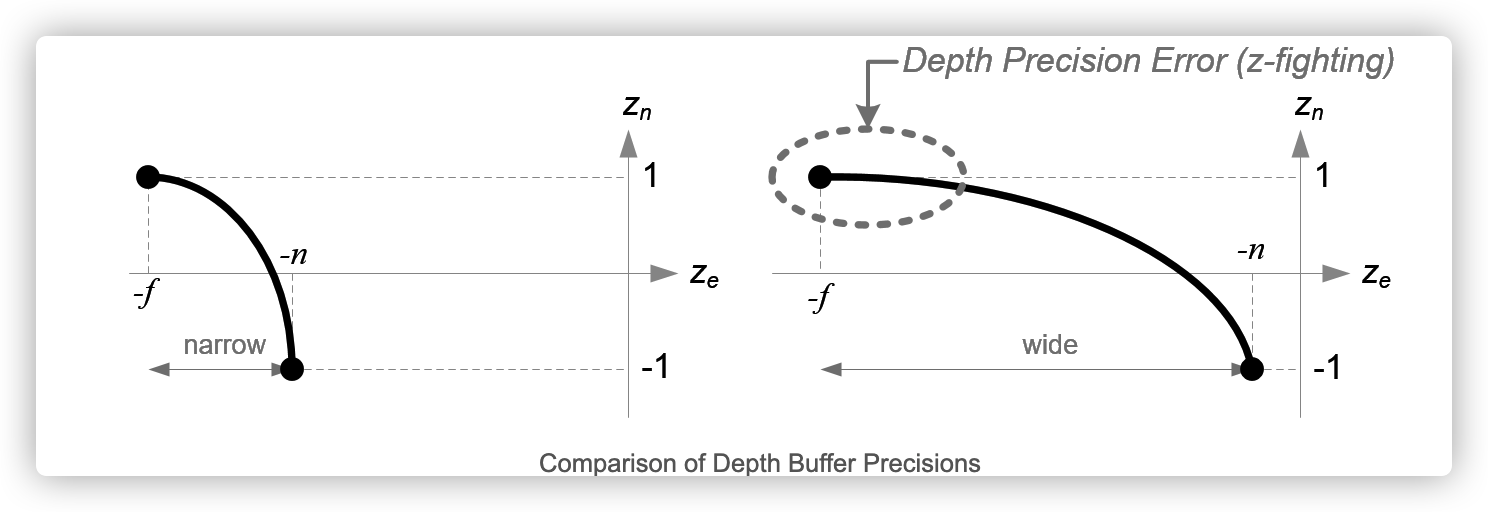
2、透视投影
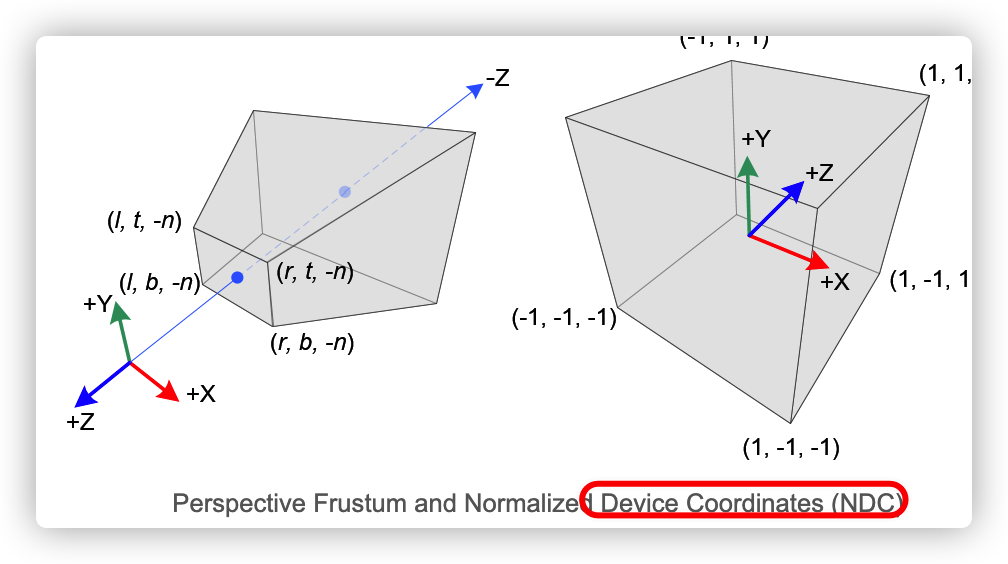

N:near
F: Far
l:left. b:Buttom
为了方便有多出来了FOV 和 Aspect
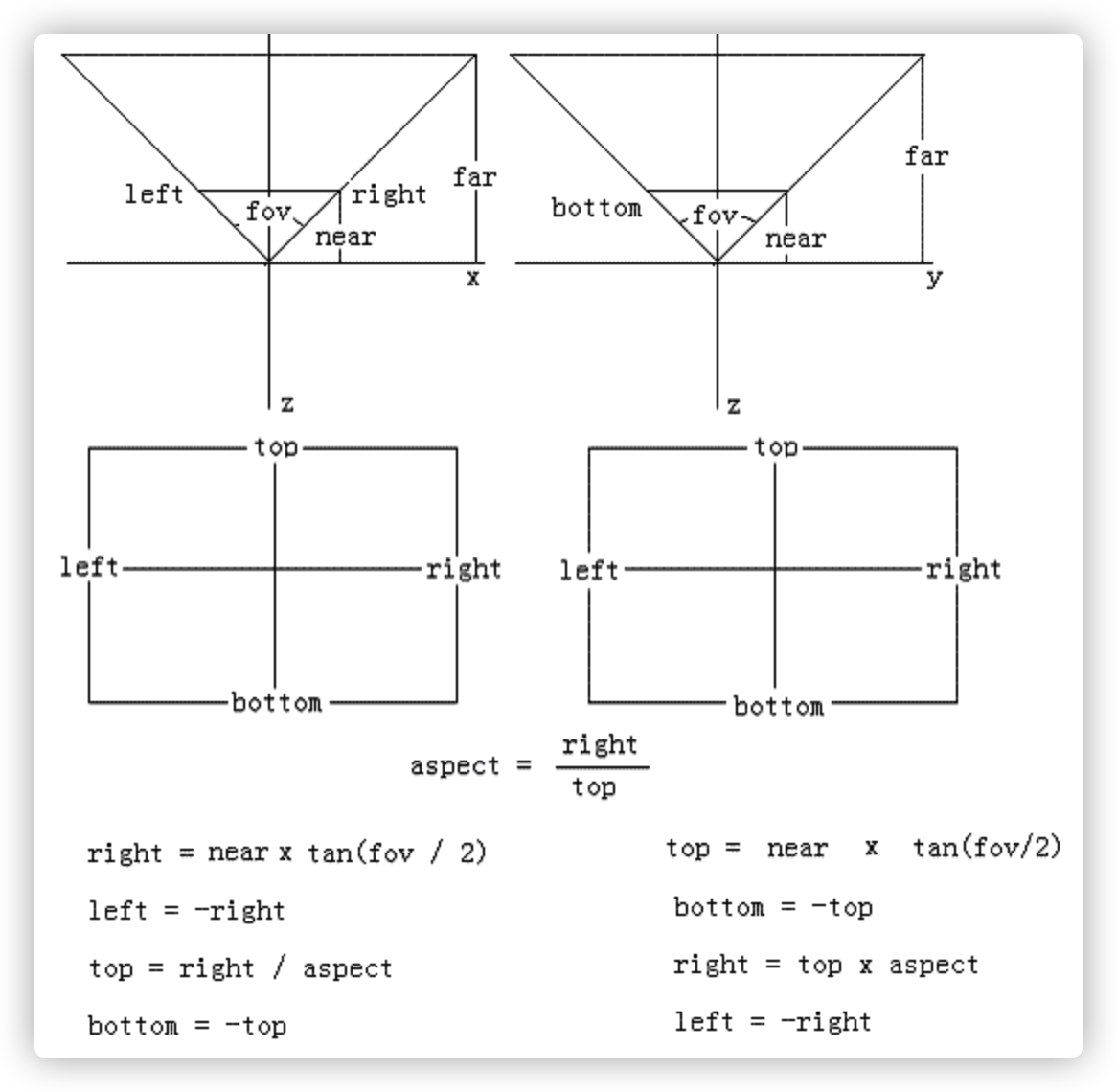
最后注意下,非线性变化.
四、额外相关的参数
这里我们存放一些屏幕分辨率, 宽度、高度、以及比例, LightPos等等方便HLSL直接使用, 减少不必要的计算.(因为VertexShader每个顶点都搞一次, Frage每个偏远都搞一次)
实现
一、ViewMatrix
嵌套方式
Matrix4x4 GetViewMatrix_TRS_Euler(Vector3 lookAtPos, Transform lightTrans, float distance)
{
Vector3 lightPos = lookAtPos - lightTrans.forward * distance;
//这里我们也可以直接用LookAt来获取Rotation
Quaternion rot =Quaternion.Euler(lightTrans.eulerAngles);
return Matrix4x4.Inverse(Matrix4x4.TRS(lightPos, rot, new Vector3(1, 1, -1)));
}
直接方式
// view矩阵, basixAxis * translate 方式 //
Matrix4x4 GetViewMatrix_AxisMulTrans(Vector3 lookAtPos, Vector3 camForward, float distance)
{
Vector3 forward = Vector3.Normalize(-camForward);
Vector3 up = new Vector3(0, 1, 0);
Vector3 right = Vector3.Normalize(Vector3.Cross(up, forward));
up = Vector3.Normalize(Vector3.Cross(forward, right));
Vector3 lightPos = lookAtPos + forward * distance;
Matrix4x4 translate = Matrix4x4.identity;
// 也可以用 Matrix4x4.Translate(-translatePos); 构建平移矩阵 //
translate.SetColumn(3, new Vector4(-lightPos.x, -lightPos.y, -lightPos.z, 1));
//translate.SetColumn(3, -lightPos);
// basicAxis //
Matrix4x4 basicAxis = Matrix4x4.identity;
basicAxis.SetRow(0, new Vector4(right.x, right.y, right.z, 0));
basicAxis.SetRow(1, new Vector4(up.x, up.y, up.z, 0));
basicAxis.SetRow(2, new Vector4(forward.x, forward.y, forward.z, 0));
// 先平移,再计算投影在基向量的长度,即新空间的坐标 //
return basicAxis * translate;
}
注意一下:
二、ProjectionMatrix
正交投影矩阵
嵌套
public static Matrix4x4 GetOrthoProjectMatrix(
float ori_left, float ori_right,
float ori_down, float ori_up,
float NearClipPlane, float FarClipPlane)
{
return Matrix4x4.Ortho(ori_left, ori_right, ori_down, ori_up, NearClipPlane, FarClipPlane);
}
直接计算
Matrix4x4 OrthoProjectMatrix(
float ori_left, float ori_right,
float ori_down, float ori_up,
float NearClipPlane, float FarClipPlane)
{
Matrix4x4 p = Matrix4x4.identity;
float h = ori_up - ori_down;
float v = ori_right - ori_left;
float n = NearClipPlane;
float f = FarClipPlane;
p.m00 = 2.0f / h; p.m01 = 0.0f; p.m02 = 0; p.m03 = 0.0f;
p.m10 = 0; p.m11 = 2.0f / v; p.m12 = 0; p.m13 = 0.0f;
p.m20 = 0; p.m21 = 0.0f; p.m22 = 1.0f / (f-n); p.m23 = n / (n-f);
p.m30 = 0; p.m31 = 0.0f; p.m32 = 0; p.m33 = 1.0f;
return p;
}
透视投影矩阵
嵌套
Matrix4x4 GetPerspectiveProjectMatrix(
float pFov, float pAspect
,float NearClipPlane, float FarClipPlane)
{
return Matrix4x4.Perspective(pFov, pAspect,NearClipPlane, FarClipPlane);
}
直接计算
略, 按照公司. 注意一下坐标系即可.
三、额外相关的参数
总结
1、通过对View和Proj的大致梳理和实现, 一来我们对一些细节有了认识.比如是否线性, 又比如方向光下的Left和Right要跟着需求做一定的变化,从而去适应(像Shadow部分, 这个包围框肯定是要跟着我们看的包围区域做变化的,不然得多大的包围才能包围住All)
2、我们有了这个, 也可以在做一些Feature时候方便计算.(比如求光照下的厚度, 比如XXX距离等等)
3、也能对我们用到的参数更熟悉,比如Aspe,FOV等等,为何RevertZ等等
4、Shadow部分不在空间变化系列,单独章节
备注
参考:
1、http://www.songho.ca/opengl/gl_projectionmatrix.html



